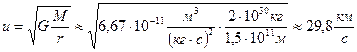Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полная механическая энергия замкнутой системы тел, в которой действуют только консервативные силы, сохраняется, не изменяется со временем.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обобщая, В замкнутой системе общее количество энергии всех видов остается строго постоянной независимо от того, какие процессы происходят в этой системе. Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этой формулировке отражены основные свойства энергии – количественная неизменность и качественная изменчивость. Закон сохранения энергии связан с однородностью времени. Однородность времени проявляется в том, что физические законы инвариантны относительно выбора начала отсчета времени, то есть они не зависят от выбора начала отсчета времени. Если в любые два момента времени замкнутую систему поставить в совершенно одинаковых условиях, то, начиная с этих моментов времени, все процессы в системе будут протекать совершенно одинаково. Например, при свободном падении тела в поле сил гравитации его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, в какой момент времени тело начало падать. Закон сохранения и превращения энергии для неизолированной системы: Изменение энергии неизолированной системы равно работе, совершаемой системой. ΔЕ=−А Если работа совершается внутренними силами самой системы, то A>0 и энергия системы убывает. Если же работа совершается внешними силами над системой, то A<0 и энергия системы возрастает. Закон сохранения и превращения энергии - фундаментальный закон природы, не имеющий исключений, выполняется и в макромире и в микромире. Неизменность полной механической энергии замкнутой системы (Е= Wк+Wр =const) приводит к тому, что мы иногда наглядно наблюдаем превращение кинетической энергии в потенциальную и наоборот (например, при колебании математического маятника). Примеры Абсолютные упругие и неупругие соударения Абсолютное упругое соударение (удар) − столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. Естественно это идеализированный случай − физическая модель. После соударения тела отделяются друг от друга и движутся самостоятельно, а кинетическая энергия перераспределяется между ними.
В данном случае соблюдаются законы сохранения импульса и механической энергии:
где m1, m2 − массы тел,
 , , 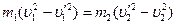 , , 
При прямого, центрального удара находим:
Абсолютное неупругое соударение − столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. При таких столкновениях часть первоначальной кинетической энергии превращается в энергию деформации, поэтому в данном случае не соблюдается закон сохранения механической энергии.
где «Потеря» кинетической энергии
Если Когда m2 >> m1, (масса неподвижного тела очень большая), то Тяготение
Закон всемирного тяготения или гравитации (Ньютон 1678г.): Материальные точки притягиваются друг к другу с силой F, пропорциональной их массам m1 и m2 и обратно пропорциональной квадрату расстояния r между ними. Точно так же, между любыми двумя материальными телами действует сила взаимного притяжения, прямо пропорциональная произведению масс этих тел и обратно пропорциональная расстояния между ними:
где G=6,67·10−11м3/кг·с2 коэффициент пропорциональности (экспериментально определил Кавендиш 1798г.). Когда m1=m2=100кг, r=1м, F≈10−6Н. Сила притяжения между Землей и Луной ~1020Н, а между молекулами (r≈3·10−10м) кислорода −~10 −32Н (разница 1052раз!). Т.е. эта сила огромно для небесных тел, ничтожна для частиц микромира и справедлив не только для материальных точек, но и для крупных тел любой формы. Сила тяжести − эта сила, которая действует на всякое тело с массой m, находящей на Земле Сила тяжести = сила гравитации. P=mg=F=G где M и R − масса и радиус Земли соответственно.
Вес тела это сила, с которой тело вследствие притяжения Земли действует на опору (или подвес), удерживающую тело от свободного падения. Невесомость, состояние, когда тело движется под действием только силы тяжести, т.е. с ускорением свободного падения. Сила тяжести действует всегда, а вес проявляется только в том случае, когда на тело кроме силы тяжести действуют еще и другие силы, вследствие чего оно движется с ускорением a≠g.
Если тело движется в поле тяготения Земли с ускорением a≠g, это означает, что не него действует дополнительная сила N и второй закон Ньютона− N+P=ma. Тогда вес тела Если тело покоится или движется прямолинейно и равномерно, то a=0, P′=mg. Если тело свободно подает в поле тяготения, то a=g, и P′=0 (невесомость). Гравитационное поле или поле тяготения является потенциальным, а силы тяготения − консервативными. С одной стороны g − ускорение свободного падения, а с другой стороны− Элементарная работа в гравитационном поле
С другой стороны, эта работа равняется изменению потенциальной энергии: A=−ΔWp=−(W2−W1)=W1−W2. Сравнивая оба значения работы, находим Потенциал поля тяготения − это скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля до бесконечности.
Эквипотенциальные поверхности для материальной точки − это сфера. ( φ=const) Связь между потенциалом (φ) поля тяготения и его напряженностью (g) определяется из dA=−mdφ и dA=Fdℓ=mgdℓ, mgdℓ=−mdφ, отсюда
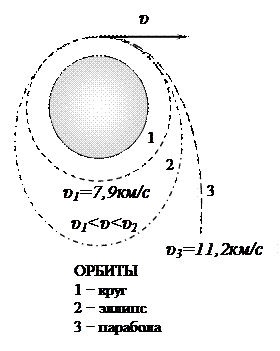
Космические скорости Для запуска ракет в космическое пространство надо им сообщить определенные начальные скорости, называемые космическими. I космической (или круговой) скоростью υ1 называют такую минимальную скорость, которую надо сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите, т.е. превратится в искусственный спутник Земли. На спутник, движущийся по круговой орбите радиусом r, действует сила тяготения Земли, сообщающая ему нормальное ускорение Вблизи Земли r=R0=~6400км, поэтому II космической (или параболической) скоростью υ2, называют ту наименьшую скорость, которую надо сообщить телу, чтобы оно оторвалось от Земли и превратилось в спутник Солнца (т.е. планету или астероид).
Отметим, что направление скорости υ2 может быть каким угодно: тело станет искусственной планетой при любом направлении скорости υ2.
Третьей космической скоростью υ3 называют скорость, которую необходимо сообщить телу на Земле, чтобы оно покинуло пределы Солнечной системы, преодолев притяжение Солнца. Формула для скорости υ3 такая же как для υ2, только центральное тело не Земля, а Солнце, поэтому из где R=1,5 108км −радиус земной орбиты, υ − скорость тела относительно Солнца.
Из этого соотношения υ = 42,2 км/с. Скорость υ можно сообщить телу в любом направлении, но очевидно, что выгоднее всего сообщить ее в направлении касательной к земной орбите, так как в этом направлении тело уже имеет относительно Солнца орбитальную скорость Земли u=29,8км/с. υ3=υ−u=12,4 км/с (υ3=υ±u=(17÷73)км/с)
υ3=16,7 км/с. Задача. Определить линейную скорость Земли u. Из равенства нормальной силы Fн и силы гравитации Fтяг между Солнцем и Землей, используя второй закон Ньютона: Fн =maн=
Четвертая космическая скорость, при которой земное тело преодолевает тяготение Галактики и может уйти во Вселенную. Расчет для υ4 сложен, но так как вокруг Солнца нет звезд, которые движутся в том же направлении как Солнце вокруг центра Галактики, и имеют больше скорости, чем 285 км/с, то можно предполагать, что это и есть четвертая космическая скорость.
Впервые в мире υ1 достигнута в СССР 1957г., а υ2 − в 1959г.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 690; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.86.209 (0.011 с.) |

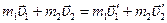 ,
, 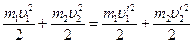 ,
, ,
,  − скорости первого тела до и после соударения,
− скорости первого тела до и после соударения, 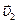 ,
,  − скорости второго тела до и после соударения.
− скорости второго тела до и после соударения.
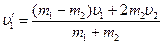

 ,
, 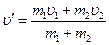 ,
,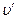 − скорость движения шаров после соударения.
− скорость движения шаров после соударения. .
.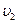 = 0, то
= 0, то  ,
,  .
.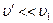 и почти вся кинетическая энергия первого тела при ударе переходит в другие формы энергии. Для значительной деформации наковальня должна быть массивнее молотка. Наоборот, при забывании гвоздей в стенку масса молотка должна быть побольше (m1>>m2), тогда
и почти вся кинетическая энергия первого тела при ударе переходит в другие формы энергии. Для значительной деформации наковальня должна быть массивнее молотка. Наоборот, при забывании гвоздей в стенку масса молотка должна быть побольше (m1>>m2), тогда 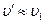 и практически вся энергия затрачивается на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.
и практически вся энергия затрачивается на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.


 ,
,
 − напряженность поля тяготения − силовая характеристикаполя гравитации и определяется силой, действующей со стороны поля на материальное тело единичной массы.
− напряженность поля тяготения − силовая характеристикаполя гравитации и определяется силой, действующей со стороны поля на материальное тело единичной массы. .
.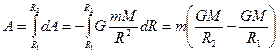 , зависит от R1 и R2
, зависит от R1 и R2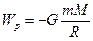
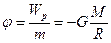
 (dℓ − элементарное перемещение).
(dℓ − элементарное перемещение).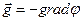 , (
, ( направлен в сторону убывания потенциала).
направлен в сторону убывания потенциала).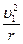 . По второму закона Ньютона:
. По второму закона Ньютона: 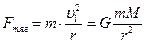 . Отсюда
. Отсюда  , т.к.
, т.к. 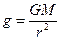
 .
. Для этого кинетическая энергия тела
Для этого кинетическая энергия тела  должна быть равна работе совершаемой против сил тяготения при перемещении тела от R0 до ∞.
должна быть равна работе совершаемой против сил тяготения при перемещении тела от R0 до ∞. и т.к.
и т.к. 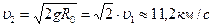

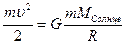 ,
, =Fтяг=
=Fтяг=  →
→