Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрическое поле. Напряженность электрического поля. Теорема Гаусса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
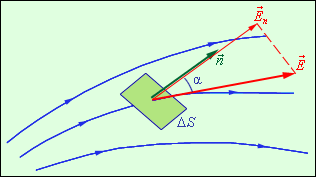
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда. Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Понятие потока вектора E аналогично понятию потока вектора скорости v при течении несжимаемой жидкости. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора E на площадь ΔS и на косинус угла α между вектором E и нормалью n к площадке называется элементарным потоком вектора напряженности через площадку ΔS (рис. 4.3.1):
где En – модуль нормальной составляющей поля E
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔSi, определить элементарные потоки
Рисунок 4.3.2. Вычисление потока Ф через произвольную замкнутую поверхность S. Теорема Гаусса утверждает: Поток вектора напряженности электростатического поля E через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
E*S=Q/E0 – Теорема Гаусса Физический смысл состоит в том, что электрическое поле всегда имеет источник и источником является заряд Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.
Билет №10 1)Силы в природе. Сила всемирного тяготения. Гравитационная постоянная. Сила тяжести. Движение искусственных спутников. Первая космическая скорость.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Но кинематика не отвечает на вопрос о причинах изменения характера движения (изменение направления, скорости тела). На эти вопросы отвечает динамика – раздел механики, изучающий взаимодействие тел. Взаимодействие тел характеризуется силами. Сила – векторная физическая величина, характеризующая взаимодействие тел. [F] = 1 Н (Ньютон). Сил в природе великое множество, но все они относятся к четырём типам взаимодействия: гравитационному, электромагнитному, сильному и слабому. Два последних – внутриядерные, к первому типу принадлежит только сила тяготения, а все остальные – электромагнитные. Силу всемирного тяготения ввёл в физику сэр Исаак Ньютон. Использовав наблюдения за движением небесных тел (в особенности Луны), он доказал, что данная сила должна в равной мере зависеть от масс обоих взаимодействующих тел и быть обратно пропорциональна квадрату расстояния. Размерностный коэффициент G – гравитационную постоянную рассчитал английский учёный Кавендиш.
- Такова векторная запись закона всемирного тяготения. Чаще применяют при расчётах скалярную запись:
Данную формулу можно применять для расчёта взаимодействия между точечными телами или между телами сферической формы. Гравитационная постоянная имеет размерность [G]=Нм2/кг2 и физический смысл силы действующей между телами массой по 1 кг на расстоянии 1 м. G = 6,67·10-11 Нм2/кг2. Как видим, эта величина мала, что показывает малость гравитационных сил.
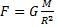 остаётся постоянной и называется g – ускорение свободного падения. g ≈ 9.8 м/с2. Тогда удобно силу всемирного тяготения записывать остаётся постоянной и называется g – ускорение свободного падения. g ≈ 9.8 м/с2. Тогда удобно силу всемирного тяготения записывать 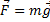 . Именуется такая сила – сила тяжести. Однако, уже движение искусственных спутников Земли проходит на высотах, на которых надо учитывать изменение силы тяготения с высотой. Впервые о возможности запускать в свободный полёт спутники сказал тоже, наверное, Ньютон. Идея проста: тело, брошенное достаточно сильно, может улететь за горизонт (рис. 1). Если бросить ещё быстрее, то ещё дальше. Ну а при определённой скорости бросания, кривизна земной поверхности вообще не даст телу упасть. Тело будет находиться в свободном падении и не падать! . Именуется такая сила – сила тяжести. Однако, уже движение искусственных спутников Земли проходит на высотах, на которых надо учитывать изменение силы тяготения с высотой. Впервые о возможности запускать в свободный полёт спутники сказал тоже, наверное, Ньютон. Идея проста: тело, брошенное достаточно сильно, может улететь за горизонт (рис. 1). Если бросить ещё быстрее, то ещё дальше. Ну а при определённой скорости бросания, кривизна земной поверхности вообще не даст телу упасть. Тело будет находиться в свободном падении и не падать!
Так движутся искусственные спутники Земли. Скорость, с которой надо лететь спутнику по круговой орбите называется первой космической скоростью.
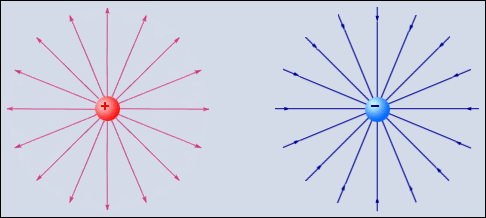
Можно трактовать первую космическую скорость как скорость кругового движения у поверхности Земли. Тогда её можно рассчитать V1 = 7,9 км/с. Если же считать, что первая космическая скорость – это круговая скорость при движении вокруг любого тела, на любом расстоянии от него, то тогда точного числа дать нельзя. Зато сфера применения формулы сильно расширяется. Так, подставив вместо массы Земли массу Солнца и расстояние от Земли до Солнца, можно рассчитать примерную скорость движения Земли по орбите – 30 км/с. 2) Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием. Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия. Электрический заряд обычно обозначается буквами q или Q. Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы: · Существует два рода электрических зарядов, условно названных положительными и отрицательными. · Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд. · Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения. Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.
Перенос заряда с заряженного тела на электрометр. Электрометр является достаточно грубым прибором; он не позволяет исследовать силы взаимодействия зарядов. Впервые закон взаимодействия неподвижных зарядов был установлен французским физиком Ш. Кулоном (1785 г.). В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора – крутильных весов (рис. 4.1.2), отличавшихся чрезвычайно высокой чувствительностью. Так, например, коромысло весов поворачивалось на 1° под действием силы порядка 10–9 Н. Идея измерений основывалась на блестящей догадке Кулона о том, что если заряженный шарик привести в контакт с точно таким же незаряженным, то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами.
Силы взаимодействия одноименных и разноименных зарядов. Прибор Кулона.
На основании многочисленных опытов Кулон установил следующий закон: Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл). Коэффициент k в системе СИ обычно записывают в виде:
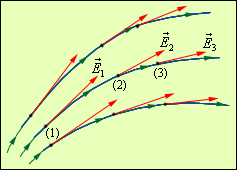
где Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции. Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел. Рис. 4.1.4 поясняет принцип суперпозиции на примере электростатического взаимодействия трех заряженных тел.
Принцип суперпозиции электростатических сил Билет №11 1)Вес тела. Невесомость и перегрузки. Вес тела, движущегося с ускорением.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Но кинематика не отвечает на вопрос о причинах изменения характера движения (изменение направления, скорости тела). На эти вопросы отвечает динамика – раздел механики, изучающий взаимодействие тел. Взаимодействие тел характеризуется силами. Сила – векторная физическая величина, характеризующая взаимодействие тел. [F] = 1 Н (Ньютон). Сил в природе великое множество, но все они относятся к четырём типам взаимодействия: гравитационному, электромагнитному, сильному и слабому. Два последних – внутриядерные, к первому типу принадлежит только сила тяготения, а все остальные – электромагнитные. Вес – сила, с которой тело действует на опору или подвес. Вес часто путают с силой тяжести и с массой. Разберём причины этой путаницы. Рассмотрим рисунок 1: тело стоит на неподвижной подставке. На тело действуют силы тяжести и нормальной реакции опоры. Эти силы уравновешены и тело неподвижно (по второму закону Ньютона). Тело действует на подставку с силой P – вес. По третьему закону Ньютона вес должен быть равен силе реакции опоры (и быть равной с ней природы, т.е. электромагнитной).
Вес равен силе реакции опоры и одновременно силе тяжести. Этот случай чаще всего встречается в жизни, и если убрать g, то вес будет равен массе (как бы равен). Отсюда путаница: «сколько весит ёжик?» «1 килограмм» J
ng w:val="-3"/><w:lang w:val="EN-US"/></w:rPr><m:t>-</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:spacing w:val="-3"/><w:lang w:val="EN-US"/></w:rPr><m:t>mg</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
Если ускорение подставки направлено вверх, то вес становится больше силы тяжести – наступает перегрузка. Перегрузки испытывают лётчики и космонавты, при подъёме своих кораблей. Боковые перегрузки испытывают гонщики на поворотах. 2)Тепловой двигатель Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Принцип работы и устройство. Для того, чтобы двигатель совершал работу, необходима разность давлений по обе стороны поршня двигателя или лопастей турбины. Во всех тепловых двигателях эта разность давлений достигается за счет повышения температуры рабочего тела на сотни или тысячи градусов по сравнению с температурой окружающей среды. Такое повышение температуры происходит при сгорании топлива. Рабочим телом у всех тепловых двигателей является газ, который совершает работу при расширении. Обозначим начальную температуру рабочего тела (газа) черезT1. В двигателях внутреннего сгорания и газовых турбинах повышение температуры происходит при сгорании топлива внутри самого двигателя. Температуру T1 называют температурой нагревателя. По мере совершения работы газ теряет энергию и неизбежно охлаждается до некоторой температуры T2. Эта температура не может быть значительно ниже температуры окружающей среды, так как в противном случае давление газа станет меньше атмосферного и двигатель не сможет работать. Обычно температура T2 несколько больше температуры окружающей среды. Ее называют температурой холодильника. В двигателе рабочее тело при расширении не может отдать всю свою внутреннюю энергию на совершение работы. Часть теплоты неизбежно передается холодильнику (атмосфере) вместе с отработанным паром или выхлопными газами двигателей внутреннего сгорания и газовых турбин. Эта часть внутренней энергии теряется. Тепловой двигатель совершает работу за счет внутренней энергии рабочего тела. При чем в этом процессе происходит передача теплоты от более горячих тел (нагревателя) к более холодным (холодильнику). Рабочее тело двигателя получает при сгорании топлива количество теплотыQ1, совершает работу A' и передает холодильнику количество теплоты Q2 < Q1. КПД Вопрос о наилучшем использовании тепловых процессов в практике возник еще в первой четверти XIX столетия. Сади Карно удалось установить условия наивыгоднейшего использования тепловых двигателей. Он показал, что КПД идеального теплового двигателя η может быть выражен формулой
т.е. он всегда меньше единицы, но тем ближе приближается к ней, чем меньше дробь Q2/Q1 (или T2/T1). Эта формула дает теоретический предел для максимального значения КПД тепловых двигателей. Она показывает, что тепловой двигатель тем эффективнее, чем выше температура нагревателя и ниже температура холодильника. Лишь при температуре холодильника, равной абсолютному нулю, КПД равен единице.
Билет № 12 1)Сила трения. Природа силы трения. Роль силы трения. Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Но кинематика не отвечает на вопрос о причинах изменения характера движения (изменение направления, скорости тела). На эти вопросы отвечает динамика – раздел механики, изучающий взаимодействие тел. Взаимодействие тел характеризуется силами. Сила – векторная физическая величина, характеризующая взаимодействие тел. [F] = 1 Н (Ньютон). Сил в природе великое множество, но все они относятся к четырём типам взаимодействия: гравитационному, электромагнитному, сильному и слабому. Два последних – внутриядерные, к первому типу принадлежит только сила тяготения, а все остальные – электромагнитные.
Кроме сухого трения скольжения существует ещё вязкое трение (наблюдается в жидкостях и газах) и трение качения (лучше говорить сопротивление качению, так как в этом случае никакого трения нет J). 2) Внутренняя энергия тела может изменяться только в результате его взаимодействия с другими телами. Существует два способа изменения внутренней энергии: теплопередача и совершение механической работы (например, нагревание при трении или при сжатии, охлаждение при расширении). Теплопередача — это изменение внутренней энергии без совершения работы: энергия передается от более нагретых тел к менее нагретым. Мерой переданной энергии при теплопередаче является количество теплоты (Q).
Адиабатный процесс (Рис.4.4). P· = Const, где = cp / cv – показатель адиабаты. A = -u = = -сv·(t2 – t1) = сv·(t1 – t2), или A = R·(T1 – T2) / ( -1); A = R·T1·[1 – ( 1/ 2) -1] /( – 1); A = R·T2·[1 – (P2/P1) ( -1)/ ] /( – 1). (4.23)
Билет №13 1)Импульс тела. Импульс силы. Изменение импульса системы взаимодействующих тел. Закон сохранения импульса. Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Очень часто при решении задач нет необходимости знать характер движения – важно лишь знать конечное состояние тела (координату и скорость). В физике существует ряд величин способных при определённых условиях сохраняться. В механике к ним относятся энергия, импульс и момент импульса.
Импульсом тела называют векторную физическую величину, характеризующую движение тела. Пусть на тело массой m действует сила F.
- Закон изменения импульса. Скорость изменения импульса равна сумме внешних сил. Закон изменения импульса можно записать и немного по другому:
Правая часть формулы иногда называется импульс силы.
После того как сформулирован закон изменения импульса легко понять и условия его сохранения: Закон сохранения импульса – импульс сохраняется в замкнутой системе тел (сумма внешних сил равна 0).
2) Внутренняя энергия — это величина, характеризующая собственное состояние тела, т.е. энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц. Внутренняя энергия одноатомного идеального газа определяется по формуле
При совершении работы в термодинамике меняется состояние макроскопических тел: их объем и температура. F - сила, действующая на газ со стороны поршня. А - работа внешних сил по сжатию газа. F’ - сила, действующая на поршень со стороны газа. А' - работа газа по расширению. F= -F’ - по 3-ему з-ну Ньютона. Следовательно: А= - А' А= pS, где p- давление, S - площадь поршня. Если газ расширяется:
h=h2 - h1 - перемещение поршня. V1=Sh1; V2=Sh2. Тогда: A'=F'h=pS(h2 - h1)=p(Sh2 - Sh1)=p(V2-V1)=pV При расширении работа газа положительна. При сжатии - отрицательна. Таким образом: A' = pV - работа газа A= - pV - работа внешних сил. Используя уравнение Менделеева-Клапейрона, получим:
Эти выражения справедливы при очень малых (!) изменениях объема или при постоянном давлении (т.е. в изобарном процессе) Физический смысл универсальной газовой постоянной.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.210.196 (0.012 с.) |

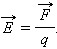
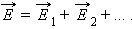
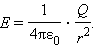
 Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор r от заряда Q к точке наблюдения. Тогда при Q > 0 вектор E параллелен r а при Q < 0 вектор E антипараллелен r Следовательно, можно записать:
Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор r от заряда Q к точке наблюдения. Тогда при Q > 0 вектор E параллелен r а при Q < 0 вектор E антипараллелен r Следовательно, можно записать: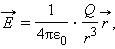
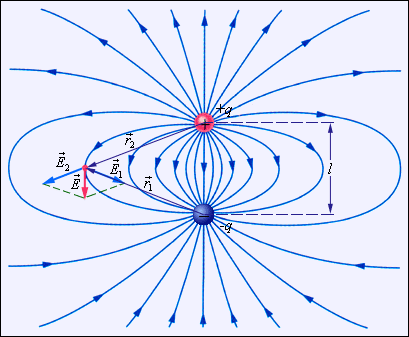
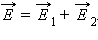
 по заданному распределению зарядов. Пусть, например, нужно найти электрическое поле длинной однородно заряженной нити (рис. 4.2.5) на расстоянии R от нее.
по заданному распределению зарядов. Пусть, например, нужно найти электрическое поле длинной однородно заряженной нити (рис. 4.2.5) на расстоянии R от нее.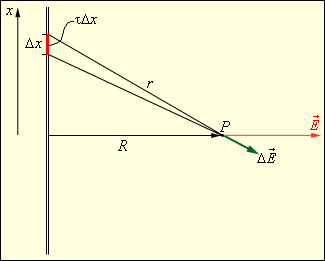 Поле в точке наблюдения P может быть представлено в виде суперпозиции кулоновских полей, создаваемых малыми элементами Δx нити, с зарядом τΔx, где τ – заряд нити на единицу длины. Задача сводится к суммированию (интегрированию) элементарных полей
Поле в точке наблюдения P может быть представлено в виде суперпозиции кулоновских полей, создаваемых малыми элементами Δx нити, с зарядом τΔx, где τ – заряд нити на единицу длины. Задача сводится к суммированию (интегрированию) элементарных полей 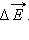 Результирующее поле оказывается равным
Результирующее поле оказывается равным 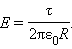
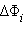 поля E через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора E через замкнутую поверхность S (рис. 4.3.2):
поля E через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора E через замкнутую поверхность S (рис. 4.3.2):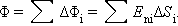
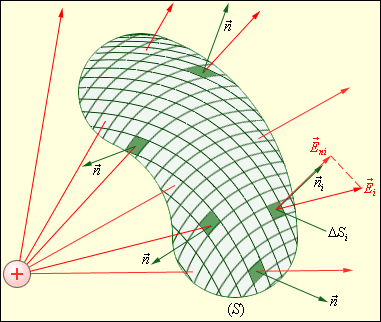 В случае замкнутой поверхности всегда выбирается внешняя нормаль.
В случае замкнутой поверхности всегда выбирается внешняя нормаль.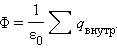
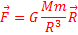
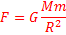
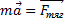
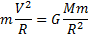
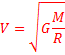
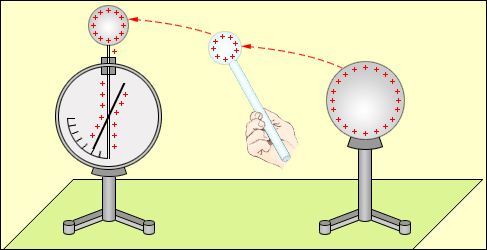 Рисунок 4.1.1.
Рисунок 4.1.1.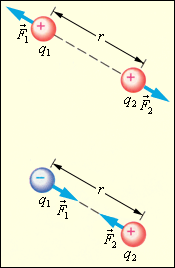 Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.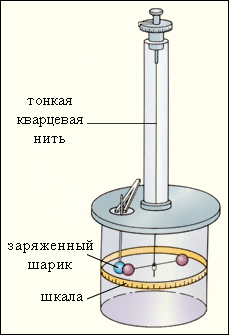 Рисунок 4.1.2. Рисунок 4.1.3.
Рисунок 4.1.2. Рисунок 4.1.3.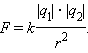
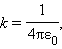
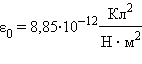 – электрическая постоянная.
– электрическая постоянная.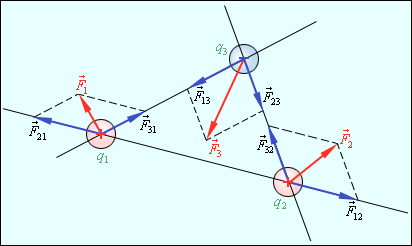 Рисунок 4.1.4.
Рисунок 4.1.4.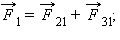
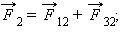
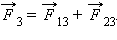
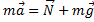
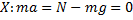
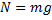
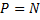
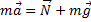
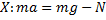
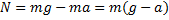
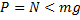
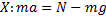
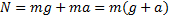
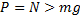
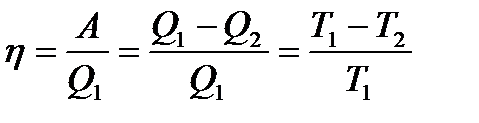 - КПД тепловых машин (последняя формула только для идеальных (машин Карно))
- КПД тепловых машин (последняя формула только для идеальных (машин Карно))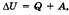 , где
, где 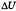 — изменение внутренней энергии, Q — количество теплоты, переданное системе, А — работа внешних сил. Если система сама совершает работу, то ее условно обозначают А’. Тогда закон сохранения энергии для тепловых процессов, который называется первым законом термодинамики, можно записать так:
— изменение внутренней энергии, Q — количество теплоты, переданное системе, А — работа внешних сил. Если система сама совершает работу, то ее условно обозначают А’. Тогда закон сохранения энергии для тепловых процессов, который называется первым законом термодинамики, можно записать так: 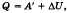 , т.е. количество теплоты, переданное системе, идет на совершение системой работы и изменение ее внутренней энергии.
, т.е. количество теплоты, переданное системе, идет на совершение системой работы и изменение ее внутренней энергии.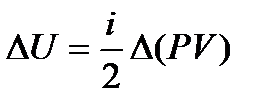 - изменение внутренней энергии идеального газа (i = 3 для одноатомного газа)
- изменение внутренней энергии идеального газа (i = 3 для одноатомного газа)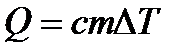 - теплота необходимая для нагрева (охлаждения) тела
- теплота необходимая для нагрева (охлаждения) тела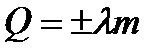 - теплота необходимая для плавления (кристаллизации)
- теплота необходимая для плавления (кристаллизации)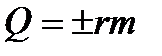 - теплота необходимая для испарения (конденсации)
- теплота необходимая для испарения (конденсации)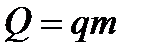 - теплота выделяющаяся при сгорании топлива
- теплота выделяющаяся при сгорании топлива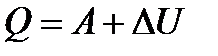 - первый закон термодинамики
- первый закон термодинамики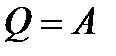 - 1-й з-н ТД для изотермического проц.
- 1-й з-н ТД для изотермического проц.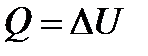 - 1-й з-н ТД для изохорного процесса
- 1-й з-н ТД для изохорного процесса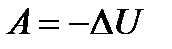 - 1-й з-н ТД для адиабатного процесса
- 1-й з-н ТД для адиабатного процесса
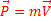 [P] = кгм/с
[P] = кгм/с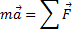
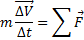
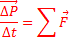
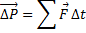
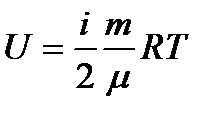 - внутренняя энергия идеального газа (i = 3 для одноатомного газа)
- внутренняя энергия идеального газа (i = 3 для одноатомного газа)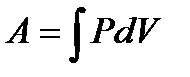 - работа газа
- работа газа