
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равнопеременное вращательное движение - вращательное движение, при котором за любые равные промежутки времени тело изменяет свою угловую скорость на одну и ту же величину.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим вращательное движение. При описании вращательного движения нас интересует не перемещение и траектория, а угловые величины (угол поворота, угловая скорость, угловое ускорение). Однако угловые величины связаны с линейными. Введём необходимые термины и величины: Период – время одного оборота [T] = 1с. Частота – число оборотов в единицу времени [х] = 1/T = 1 Гц. Угловая скорость – быстрота поворота тела (быстрота прохождения угла)
Угловое ускорение – быстрота изменения угловой скорости.
Связи между угловыми и линейными величинами:
Для равноускоренного движения по окружности будут справедливы формулы, визуально и математически аналогичные таковым для равноускоренного движения по прямой:
RRS и VAVB ДV (оба треугольника равнобедренные и углы между сторонами равны). Значит:
Теперь будем уменьшать рассматриваемый промежуток времени. При стремлении его к 0 перемещение и путь практически совпадают:
2) Твердые тела могут существовать в двух существенно различных состояниях, отличающихся своим внутренним строением, и, соответственно, свойствами. Это кристаллическое и аморфное состояние твердых тел. Кристаллическое состояние характеризуется наличием четко выделяемых естественных граней, образующих между собой определенные углы. Примерами веществ в кристаллическом состоянии могут служить соль, сахарный песок, сода и др. Если весь кусок вещества представляет собой один кристалл, то такое тело называется монокристаллом или просто кристаллом. В других случаях тело представляет собой множество мелких кристалликов, причудливо сросшихся между собой, например, кусок рафинада. Такие тела называют поликристаллическими. Наличие естественных граней у монокристаллов ведет к четко выраженному различию в физических свойствах тела по различным направлениям (анизотропия). Это может относиться к механической прочности, тепло- и электропроводности, упругости и т.д. Но не всегда все свойства зависят от направления - кубический кристалл меди обладает одинаковой электропроводностью по всем направлениям, но разной упругостью. Монокристалл ценны как материал, обладающий особыми физическими свойствами. Например, алмаз и боразон предельно тверды, флюорит прозрачен для широкого диапазона длин волн, кварц - пьезоэлектрик. Монокристалл способны менять свои свойства под влиянием внешних воздействий (света, механических напряжений, электрических и магнитного полей, радиации, температуры, давления). Поэтому изделия и элементы, изготовленные из Монокристаллов, применяются в качестве различных преобразователей в радиоэлектронике, квантовой электронике, акустике, вычислительной технике и др. Второй вид твердого состояния твердых тел - аморфное состояние. В этом состоянии невозможно обнаружить даже малые области, в которых наблюдалась бы зависимость физических свойств от направления. Некоторые вещества могут находиться в любом из этих двух состояний.
Билет №6 1)Свободное падение тел. Ускорение свободного падения. Движение тела, брошенного под углом к горизонту.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения.
При свободном падении тела, движение происходит под действием только силы тяжести. Тогда, согласно второму закону Ньютона:
В проекции на ось, направленную к центру планеты получим:
ng w:val="-3"/></w:rPr><m:t>g</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> - ускорение свободного падения. Для Земли это ускорение равно приблизительно 9,82 м/с2. Но величина g меняется из-за действия разных факторов. Самый главный – широта. С уменьшением широты g уменьшается по двум причинам: из-за вращения Земли и из-за сплюснутости Земли. Кроме этих факторов действуют и локальные причины изменения ускорения свободного падения. В первую очередь, это разная плотность пород, залегающих в данной местности. Если в каком – либо месте есть залежи металлических руд, то плотность грунта в этих местах повышена и g больше. Так как ускорение тела не меняется при движении на небольших расстояниях от поверхности Земли, то для описания подходят формулы равноускоренного движения.
Выразим время:
Как видим, полученное уравнение есть уравнение параболы с ветвями, направленными вниз. Да и на рисунке так же J. Интересно отметить некоторые закономерности движения тела по параболе (при старте и финише на одной высоте): 1. В силу симметричности данной кривой тело на старте имеет такую же скорость (по величине и углу) как и на финише; 2. Время подъёма на максимальную высоту равно времени спуска на землю; 3. В верхней точке вертикальная компонента скорости равна 0; 4. Максимальная дальность полёта достигается при угле вылета 450 и равна при этом «учетверённой» высоте подъёма. 2) Электрическая емкость. Конденсаторы.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.237.229 (0.009 с.) |

 ; [щ] = 1рад/с
; [щ] = 1рад/с ; [е] = 1 рад/с2
; [е] = 1 рад/с2





 . Теперь:
. Теперь: и
и  .
.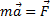








 и подставим его в уравнение для перемещения по оси Y. Кроме того, пользуясь тем, что начальные координаты у нас равны 0, мы можем приравнять перемещения по осям X и Y и координаты X и Y:
и подставим его в уравнение для перемещения по оси Y. Кроме того, пользуясь тем, что начальные координаты у нас равны 0, мы можем приравнять перемещения по осям X и Y и координаты X и Y:



