
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поле однородно заряженной сферыСодержание книги
Поиск на нашем сайте
Поле объемного заряженного шара
Билет №2 1)Равномерное прямолинейное движение. Скорость. Координаты, пройденный путь при равномерном прямолинейном движении. Графики скорости, пути и координаты равномерного прямолинейного движения.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Движение тел в природе бесконечно разнообразно и сложно для описания. Для упрощения мы создаём идеализированные модели, одной из которых является равномерное прямолинейное движение. Равномерным называется такое движение, при котором за любые равные промежутки времени тело проходит равные расстояния. Прямолинейное движение происходит, понятно, по прямой линии. Можно определить равномерное прямолинейное движение, как движение, при котором вектор скорости остаётся постоянным. Скорость – быстрота изменения положения тела в пространстве (векторная физическая величина).
Рассмотрим ситуацию, при которой тело движется вдоль определённой оси Х (рис. 1) Исходя из формулы (1), получим: Спроецируем данное уравнение на ось Х:
2) Наиболее интересной особенностью жидкостей является наличие свободной поверхности. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости. Если молекула переместиться с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (т. е. увеличить площадь поверхности жидкости), надо затратить положительную работу внешних сил ΔAвнеш, пропорциональную изменению ΔS площади поверхности: ΔAвнеш = σΔS Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу. В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или в ньютонах на метр (1 Н/м = 1 Дж/м2). Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия Ep поверхности жидкости пропорциональна ее площади:
Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Отсюда следует, что свободная поверхность жидкости стремится сократить свою площадь. По этой причине свободная капля жидкости принимает шарообразную форму. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются силами поверхностного натяжения. Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку, с той только разницей, что упругие силы в пленке зависят от площади ее поверхности (т. е. от того, как пленка деформирована), а силы поверхностного натяжения не зависят от площади поверхности жидкости. Некоторые жидкости, как, например, мыльная вода, обладают способностью образовывать тонкие пленки. Всем хорошо известные мыльные пузыри имеют правильную сферическую форму – в этом тоже проявляется действие сил поверхностного натяжения. Если в мыльный раствор опустить проволочную рамку, одна из сторон которой подвижна, то вся она затянется пленкой жидкости (рис. 3.5.3).
Силы поверхностного натяжения стремятся сократить поверхность пленки. Для равновесия подвижной стороны рамки к ней нужно приложить внешнюю силу Fвнеш=-Fн. Если под действием силы Fвнеш перекладина переместиться на Δx, то будет произведена работа ΔAвнеш = FвнешΔx = ΔEp = σΔS, где ΔS = 2LΔx – приращение площади поверхности обеих сторон мыльной пленки. Так как модули сил
Коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность. Из-за действия сил поверхностного натяжения в каплях жидкости и внутри мыльных пузырей возникает избыточное давление Δp. Если мысленно разрезать сферическую каплю радиуса R на две половинки, то каждая из них должна находиться в равновесии под действием сил поверхностного натяжения, приложенных к границе 2πR разреза, и сил избыточного давления, действующих на площадь πR2 сечения (рис. 3.5.4). Условие равновесия записывается в виде
Отсюда избыточное давление внутри капли равно
Избыточное давление внутри мыльного пузыря в два раза больше, так как пленка имеет две поверхности:
Билет №3 1)Равноускоренное движение. График зависимости ускорения, скорости, пути от времени при движении. Ускорение.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения.
Ускорение – быстрота изменения скорости.
[a] = 1м/с2
Взяв за основу формулу ускорения, определим закон изменения скорости тела:
Если ускорение направлено вдоль оси движения тела, то в проекции на эту ось:
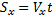 . Применим понятие мгновенной скорости, и будем уменьшать рассматриваемый интервал времени Дt. При малых временах изменение скорости будет почти незаметным, и вместо куска наклонной линии можно ввести кусок горизонтальной. Но тогда площадь под этим куском графика будет численно равна перемещению тела за этот очень малый промежуток времени. Если же теперь сложить эти малые перемещения, то мы с одной стороны, получим общее перемещение тела, а с другой стороны, площадь под кривой скорости (трапеция) (рис.2). Найдем эту площадь (перемещение тела). . Применим понятие мгновенной скорости, и будем уменьшать рассматриваемый интервал времени Дt. При малых временах изменение скорости будет почти незаметным, и вместо куска наклонной линии можно ввести кусок горизонтальной. Но тогда площадь под этим куском графика будет численно равна перемещению тела за этот очень малый промежуток времени. Если же теперь сложить эти малые перемещения, то мы с одной стороны, получим общее перемещение тела, а с другой стороны, площадь под кривой скорости (трапеция) (рис.2). Найдем эту площадь (перемещение тела).
(Дt заменено на t, так как при отсчёте от 0 эти величины равны). Если расписать проекцию перемещения через начальную и конечную координаты, то получим уравнение координаты при равноускоренном движении:
Математически – это уравнение параболы.
2) Вблизи границы между жидкостью, твердым телом и газом форма свободной поверхности жидкости зависит от сил взаимодействия молекул жидкости с молекулами твердого тела. Если эти силы больше сил взаимодействия между молекулами самой жидкости, то жидкость смачивает поверхность твердого тела. В этом случае жидкость подходит к поверхности твердого тела под некоторым острым углом θ. Угол θ называется краевым углом. Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела, то краевой угол θ оказывается тупым (рис. 3.5.5). В этом случае говорят, что жидкость не смачивает поверхность твердого тела. При полном смачивании θ = 0, при полном несмачивании θ = 180°.
Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются. На рис. 3.5.6 изображена капиллярная трубка некоторого радиуса r, опущенная нижним концом в смачивающую жидкость плотности ρ. Верхний конец капилляра открыт. Подъем жидкости в капилляре продолжается до тех пор, пока сила тяжести Fт действующая на столб жидкости в капилляре, не станет равной по модулю результирующей Fн сил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: Fт = Fн, где Fт = mg = ρhπr2g, Fн = σ2πr cos θ. Отсюда следует:
При полном смачивании θ = 0, cos θ = 1. В этом случае
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр. Вода практически полностью смачивает чистую поверхность стекла. Наоборот, ртуть полностью не смачивает стеклянную поверхность. Поэтому уровень ртути в стеклянном капилляре опускается ниже уровня в сосуде. 1) Равномерное движение точки по окружности. Центростремительное ускорение. Тангенциальное, нормальное и полное ускорение.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения.
Рассмотрим чисто вращательное движение, причём с постоянной по модулю скоростью. Введём необходимые термины и величины: Период – время одного оборота [T] = 1с. Частота – число оборотов в единицу времени [х] = 1/T = 1 Гц. Угловая скорость – быстрота поворота тела (быстрота прохождения угла)
RRS и VAVB ДV (оба треугольника равнобедренные и углы между сторонами равны). Значит:
Теперь будем уменьшать рассматриваемый промежуток времени. При стремлении его к 0 перемещение и путь практически совпадают:
Их векторная сумма определяет полное ускорение тела, движущегося по криволинейной траектории. 2)Насы́щенный пар — пар, находящийся в термодинамическом равновесии с жидкостью или твёрдым телом того же состава. Между жидкостью и её Н.п. существует динамическое равновесие: число молекул, вырывающихся в единицу времени из жидкости и переходящих в паровую фазу, равно числу молекул пара, возвращающихся в жидкость за то же время. В интервале температур и давлений, в котором возможно термодинамическое равновесие жидкости с паром, каждому давлению соответствует определённая температура насыщения пара. Определённая зависимость связывает также плотности жидкости и Н. п. С увеличением температуры увеличиваются давление и плотность Н. п. и уменьшается плотность жидкости. При равенстве внешнего давления давлению насыщенного пара происходит кипение жидкости. Практический интерес представляет умение измерять количество водяного пара в воздухе при заданной температуре. Масса водяного пара в единице объема воздуха называется абсолютной влажностью. Парциальное давление р водяного пара при данной температуре никогда не может быть больше давления насыщенного пара pнасыщ при этой же температуре. Соответствующие значения рнасыщ берутся из таблиц. Температура, при которой водяной пар в воздухе становится насыщенным, называется точкой росы. Относительной влажностью воздуха при данной температуре называется выраженное в процентах отношение парциального давления водяного пара к давлению насыщенного пара при этой же температуре: j = р/рнасыщ 100%. Простой прибор, измеряющий относительную влажность, это психрометр. Он состоит из двух термометров, один из которых сухой, а второй обмотан кусочком влажной ткани, другой конец которой опущен в воду. Сухой термометр всегда показывает температуру воздуха. Чем больше относительная влажность, тем меньше испарение воды и, следовательно, тем меньше охлаждение влажного термометра. Поэтому влажный термометр всегда показывает меньшую температуру, чем сухой, но эти показания зависят от интенсивности испарения, а следовательно, от абсолютной влажности воздуха. Если влажность равна 100%, показания обоих термометров совпадают. По специально составленным таблицам можно определить относительную влажность по разности показаний термометров.
Билет №5 1)Равнопеременное вращательное движение. Связь линейных величин с угловыми.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Движение тел в природе бесконечно разнообразно и сложно для описания. Для упрощения мы создаём идеализированные модели. Например, мы разделяем поступательное и вращательное движения. При поступательном движении тела все его точки движутся по одинаковым траекториям, а при вращательном - по разным.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.142.113 (0.009 с.) |


 или
или  .
при r > R. Если r < R, то
.
при r > R. Если r < R, то  ; E=0.
; E=0.
 - объемная плотность заряда
- объемная плотность заряда 

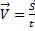 (1)
(1)
 – получим уравнение координаты для равномерного движения. Перемещение, тела, определяется как: S
– получим уравнение координаты для равномерного движения. Перемещение, тела, определяется как: S  . Путь, пройденный телом, определяется как: L
. Путь, пройденный телом, определяется как: L  . Заметим, что в начальный момент времени пут и перемещение тела обязательно равны 0. Кроме того, путь, в отличие от перемещения, – величина всегда положительная и неубывающая. Данные зависимости удобно представлять графически. Решим, для примера, задачу: Тело движется вдоль оси Х так, что скорость его меняется как показано на графике Vx(t). Нарисовать графики зависимости координаты,
. Заметим, что в начальный момент времени пут и перемещение тела обязательно равны 0. Кроме того, путь, в отличие от перемещения, – величина всегда положительная и неубывающая. Данные зависимости удобно представлять графически. Решим, для примера, задачу: Тело движется вдоль оси Х так, что скорость его меняется как показано на графике Vx(t). Нарисовать графики зависимости координаты, 
 и
и  одинаковы, можно записать:
одинаковы, можно записать:









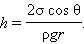

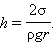
 ; [щ] = 1рад/с
; [щ] = 1рад/с
 . Теперь:
. Теперь: и
и  .
.


