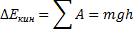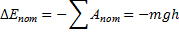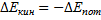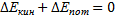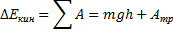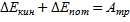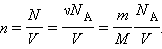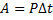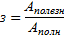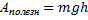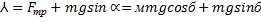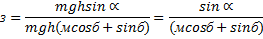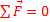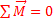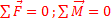Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Универсальная газовая постоянная численно равна работе 1 моля идеального газа при изобарном нагревании на 1 К.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Геометрическое истолкование работы. В изобарном процессе площадь под графиком в координатах p,V численно равна работе В общем случае надо процесс разбить на малые части и сосчитать элементарные работы, а затем их сложить
Билет №14 1)Работа силы. Кинетическая энергия. Теорема о кинетической энергии.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Очень часто при решении задач нет необходимости знать характер движения – важно лишь знать конечное состояние тела (координату и скорость). В физике существует ряд величин способных при определённых условиях сохраняться. В механике к ним относятся энергия, импульс и момент импульса.
Пусть на тело действует сила F. Тело под действием этой силы совершит перемещение S. Тогда можно сказать, что сила совершила механическую работу:
Круглые скобки обозначают скалярное произведение векторов. В скалярном виде эта формула выглядит:
где угол б – есть угол между силой и перемещением тела. Угол этот может быть любым, но для некоторых сил он практически всегда фиксирован. Так для силы трения (сопротивления) этот угол всегда 1800, и как следствие, работа этих сил всегда отрицательна. Для силы нормальной реакции опоры этот угол – 900, и работа этой силы 0. [A] = 1 Дж. Рассмотрим опять рисунок 1. Тело, под воздействием силы, приобретает ускорение:
Спроецируем на ось направленную по движению тела:
И для случая действия нескольких сил:
Слева в выражении появилось изменение некоторой величины. Эта величина называется кинетическая энергия – скалярная физическая величина, характеризующая движение тела. [Eк] = 1 Дж. Энергия вообще (и кинетическая, в частности) характеризует способность тела (или системы тел) совершить работу. Данное выражение называется Теорема о Кинетической Энергии – изменение кинетической энергии равно сумме работ внешних сил. 2) Твердым телом в механике называется неизменимая система материальных точек, т.е. такая идеализированная система, при любых движениях которой взаимные расстояния между материальными точками системы остаются неизменными. Силы притяжения и отталкивания обуславливают механическую прочность твердых тел, т.е. их способность противодействовать изменению формы и объема. Растяжению тел препятствуют силы межатомного притяжения, а сжатию - силы отталкивания. Недеформируемых тел в природе не существует. Деформация - изменение формы или объема тела под действием внешних сил. Деформацию растяжения и сжатия можно охарактеризовать абсолютной деформацией ℓ, равной разности длин образца после растяжения ℓ и до него ℓ0: ℓ = ℓ – ℓ0
ℓ = ℓ – ℓ0 Отношение абсолютной деформации ℓ к первоначальной длине образца ℓo называют относительной деформацией: Из опыта: С учетом направления: Билет №15 1)Работа силы тяжести. Потенциальная энергия тела, поднятого над поверхностью Земли. Потенциальная энергия тела в гравитационном поле.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Очень часто при решении задач нет необходимости знать характер движения – важно лишь знать конечное состояние тела (координату и скорость). В физике существует ряд величин, способных при определённых условиях сохраняться. В механике к ним относятся энергия, импульс и момент импульса.
Рассмотрим рисунок 1. Первый раз уроним J тело вертикально. Оно пролетит h, и сила тяжести совершит работу
Если теперь скатить тело по наклонной плоскости, то перемещение тела будет S, а работа силы тяжести:
то есть не изменится. Легко понять, что если спускать тело по любой произвольной траектории L, то работа будет опять та же самая, т.к. любую траекторию можно разбить на наклонные участки, а работу на таком участке мы уже просчитали. Значит, работа силы тяжести не зависит от формы траектории, а зависит только от начального и конечного положения тела. Такие силы называют потенциальными или консервативными. Кроме силы тяжести, к потенциальным силам относятся силы упругости, Кулона. Рассмотрим тело (кирпич), поднятое над Землёй на высоту h. Если его отпустить, то оно разгонится и приобретёт кинетическую энергию. Если это тело потом остановить (головой, например J), то оно совершит работу. Значит, тело, поднятое над Землёй, обладает энергией, потенциальной энергией.
Мы видим, что с высотой потенциальная энергия возрастает. Когда тело падает, то его потенциальная энергия убывает, и оно совершает работу. Таким образом, мы можем сформулировать теорему о потенциальной энергии:
Работа потенциальных сил равна изменению потенциальной энергии, взятой с обратным знаком (убыли). К сожалению, такие простые выражения для потенциальных энергий получаются только для простых потенциальных сил. В случае, когда сила сама зависит от пройденного телом расстояния, выражения усложняются. Так для расчёта потенциальной энергии тела в гравитационном (межпланетном) поле потребуется взятие интеграла. Вид же её не сложен:
Обратим внимание на знак минус – потенциальная энергия сил притяжения всегда отрицательная. 2) Агрегатное состояние — состояние вещества, характеризующееся определёнными качественными свойстваи — способностью или неспособностью сохранять объём и форму, наличием или отсутствием дальнего и ближнего порядка и другими. Изменение агрегатного состояния сопровождается скачкообразным изменением свободной энергии, энтропии, плотности и других основных физических свойств. Выделяют следующие агрегатные состояния: Твёрдое тело Состояние, характеризующееся способностью сохранять объём и форму. Атомы твёрдого тела совершают лишь небольшие колебаия вокруг состояния равновесия. Присутствует как дальний, так и ближний порядок. Жидкость Состояние вещества, при котором оно обладает малой сжимаемостью, то есть хорошо сохраняет объём, однако однако неспособно сохранять форму. Жидкость легко принимает форму сосуда, в которую она помещена. Атомы или молекулы жидкости совершают колебания вблизи состояния равновесия, запертые другими атомами, и часто перескакивают на другие свободные места. Присутствует только ближний порядок. Газ Состояние, характеризующееся хорошей сжимаемостью, отсутствием способности сохранять как объём, так и форму. Газ стремится занять весь объём, ему предоставленный. Атомы или молекулы газа ведут себя относительно свободно, расстояния между ними гораздо больше их размеров. Твёрдое и жидкие состояния вещества относятся к конденсированным состояниям — атомы или молекулы вещества в них находятся настолько близко друг к другу, что неспособны свободно двигаться. Изменение агрегатного состояния — термодинамические процессы, являющиеся фазовыми переходами. Выделяют следующие их разновидности: из твёрдого в жидкое — плавление; из жидкого в газообразное — испарение и кипение; из твёрдого в газообразное — сублимация; из газообразного в жидкое или твёрдое — конденсация.
Билет №16 1)Работа силы упругости. Потенциальная энергия деформированной пружины. Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Очень часто при решении задач нет необходимости знать характер движения – важно лишь знать конечное состояние тела (координату и скорость). В физике существует ряд величин, способных при определённых условиях сохраняться. В механике к ним относятся энергия, импульс и момент импульса. Известно, что формула механической работы имеет вид:
трапеции:
Обратим внимание на то, что получившееся выражение выглядит как убыль некоторой величины. Если вспомнить теорему о потенциальной энергии, то получается, что эта величина есть потенциальная энергия упруго деформированного тела:
2) Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (p, V и T). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах p, V) в виде некоторой траектории, каждая точка которой представляет равновесное состояние. Интерес представляют процессы, в которых один из параметров (p, V или T) остается неизменным. Такие процессы называются изопроцессами.
V= Const, 2 = 1. (4.10) Уравнение состояния процесса: P2 / P1 = T2 / T1. (4.11) Так как υ 2 = υ 1, то A = 0 и уравнение 1-го закона т/д имеет вид: q = u = = сv·(t2 - t1); (4.12)
2 / 1 = T2 / T1, (4.13) Работа этого процесса: A = P·( 2 - 1). (4.14) Уравнение 1-го закона т/д имеет вид: q = u + A = ср·(t2 - t1); (4.15)
Т = Const, Т2 = Т1 Уравнение состояния: P1 / P2 = 2 / 1, (4.16) Так как Т2 = Т1, то u = 0 и уравнение 1-го закона т/д будет иметь вид: q = A = R·T·ln( 2/ 1), (4.17) или q = A = R·T·ln(P1/P2), (4.18) где R = R/ – газовая постоянная [Дж/(кг·К)].
P· = Const, (4.19) где = cp / cv – показатель адиабаты. A = -u = = -сv·(t2 – t1) = сv·(t1 – t2), (4.20) или A = R·(T1 – T2) / ( -1); (4.21)
Билет №17 1)Полная энергия тела. Изменение энергии системы тел под действием внешних сил. Закон сохранения полной механической энергии.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Очень часто при решении задач нет необходимости знать характер движения – важно лишь знать конечное состояние тела (координату и скорость). В физике существует ряд величин, способных при определённых условиях сохраняться. В механике к ним относятся энергия, импульс и момент импульса.
Рассмотрим рисунок 1. Тело скользит по наклонной плоскости (сначала без трения). Работа силы нормальной реакции опоры равна 0, работа силы тяжести A = mgh. По теореме о кинетической энергии:
По теореме о потенциальной энергии:
- при действии на систему только внутренних потенциальных сил полная (кинетическая + потенциальная) энергия сохраняется. Теперь предположим, что на тело действует сила трения:
Если бы на тело действовали и другие внешние или непотенциальные силы, то изменение полной энергии было бы равно сумме работ этих сил. Закон изменения полной механической энергии: изменение полной механической энергии равно суме работ внешних и внутренних непотенциальных сил. Из этого закона совершенно логично вытекает и ЗАКОН СОХРАНЕНИЯ ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ: полная механическая энергия сохраняется в замкнутой и консервативной системе. 2) Соотношение
связывающее давление газа с его температурой и концентрацией молекул, для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
Здесь N – число молекул в сосуде, NA – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
Произведение постоянной Авогадро NA на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть:
Соотношение
называется уравнением состояния идеального газа.
Билет №18 1)Механическая работа и мощность. КПД (на примере наклонной плоскости).
Круглые скобки обозначают скалярное произведение векторов. В скалярном виде эта формула выглядит:
где угол б – есть угол между силой и перемещением тела. Угол этот может быть любым, но для некоторых сил он практически всегда фиксирован. Так для силы трения (сопротивления) этот угол всегда 1800, и как следствие, работа этих сил всегда отрицательна. Для силы нормальной реакции опоры этот угол – 900, и работа этой силы 0. [A] = 1 Дж. В реальной жизни очень важным является то, как быстро мы можем совершить работу. Поэтому для выкапывания большой ямы задействуют экскаватор, а для перевозки грузов – большие машины или железнодорожные поезда. Скорость совершения работы в физике – это мощность.
[P] = 1 Вт (в честь Джеймса Уатта (Watt)). Из вышеприведённой формулы следует возможность введения ещё одной единицы работы:
[A] = 1 Вт∙с Дело в том, что в технике работу гораздо проще измерить, зная мощность механизма и время его работы. Только, поскольку в жизни все механизмы гораздо большей мощности, чем 1 Вт и работают они не секунды, а часы, то применяют кратную единицу - кВт∙час. 1 кВт∙час = 3600000 Дж. При производстве работ, к сожалению, часть энергии расходуется зря (на преодоление сопротивления среды). Поэтому, любой механизм характеризуется КПД – коэффициентом полезного действия – отношение полезной работы к полной (совершённой):
Если поднимать тело медленно (без разгона), то:
где µ - коэффициент трения тела о плоскость. Таким образом:
Проанализируем полученную формулу. Во-первых, КПД будет тем больше, чем больше угол наклона плоскости и чем меньше трение. Во-вторых, при отсутствии трения, КПД = 100%, но такого не бывает в природе. Таким образом, жизнь ставит нам, как всегда, задачу оптимизации: с одной стороны, чем меньше наклон – тем больше должен быть выигрыш в силе, а с другой стороны, тем меньше КПД. Поэтому трубы, бочки, баллоны и другие «круглые» тела стараются закатывать наверх по наклонной плоскости (сопротивление качения мало), а прямоугольные ящики чаще просто поднимают (трение скольжения для них большое). 2) Температура — скалярная физическая величина, описывающая состояние термодинамического равновесия (состояния, при котором не происходит изменения микроскопических параметров). Как термодинамическая величина температура характеризует тепловое состояние системы и измеряется степенью его отклонения от принятого за нулевое. Как молекулярно-кинетическая величина — характеризует интенсивность хаотического движения молекул и измеряется их средней кинетической энергией. Ек = 3/2 kT, где k = 1,38 • 10^(-23) Дж/К и называется постоянной Больцмана. Температура всех частей изолированной системы, находящейся в равновесии, одинакова. Измеряется температура термометрами в градусах различных температурных шкал. Существует абсолютная термодинамическая шкала (шкала Кельвина) и различные эмпирические шкалы, которые отличаются начальными точками. До введения абсолютной шкалы температур в практике широкое распространение получила шкала Цельсия (за О °С принята точка замерзания воды, за 100 °С принята точка кипения воды при нормальном атмосферном давлении). Единица температуры по абсолютной шкале называется Кельвином и выбрана равной одному градусу по шкале Цельсия 1 К = 1 °С. В шкале Кельвина за ноль принят абсолютный ноль температур, т. е. температура, при которой давление идеального газа при постоянном объеме равно нулю. Вычисления дают результат, что абсолютный нуль температуры равен -273 °С. Таким образом, между абсолютной шкалой температур и шкалой Цельсия существует связь Т = t °C + 273. Абсолютный нуль температур недостижим, так как любое охлаждение основано на испарении молекул с поверхности, а при приближении к абсолютному нулю скорость поступательного движения молекул настолько замедляется, что испарение практически прекращается. Теоретически при абсолютном нуле скорость поступательного движения молекул равна нулю, т. е. прекращается тепловое движение молекул.
Билет №19 1)Равновесие твердых тел при отсутствии вращения. Условие равновесия тела с закрепленной осью вращения. Момент силы. Условие равновесия твердого тела.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения. Но механика изучает также и стационарные (равновесные) состояния – состояния движения тела, которые могут сохраняться неопределённо долго при отсутствии внешнего воздействия. Такие состояния изучает СТАТИКА.
(Это не вполне корректное выражение, но пока сойдёт J). [M] = 1 Нм. Существует три вида равновесия: устойчивое, неустойчивое и безразличное. Устойчивое равновесие (рис. 2) – положение тела, при котором при малом отклонении тела от положения равновесия возникают силы или моменты сил, возвращающие тело в положение равновесия. Неустойчивое равновесие (рис. 3) – положение тела, при котором при малом отклонении тела от положения равновесия возникают силы или моменты сил, увеличивающие это отклонение. Безразличное равновесие (рис. 4) – положение тела, при котором при малом отклонении тела от положения равновесия новых сил или моментов сил не возникает.
Так же существуют три типа движения тела, при которых мы рассматриваем равновесие: поступательное, вращательное (с закреплённой осью) и свободное. Для каждого типа движения условия равновесия различаются. Условия равновесия: 1. Поступательное движение – сумма сил, действующих на тело должна быть равна 0. 2. Вращательное движение – сумма моментов сил, действующих на тело должна быть равна 0. 3. Свободное движение – сумма сил и моментов сил, действующих на тело должна быть равна 0. И, в заключение надо отметить, что это были силовые критерии равновесия. Можно сформулировать энергетические критерии: в положении устойчивого равновесия энергия тела минимальна, а в положении неустойчивого – максимальна.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.68.161 (0.016 с.) |



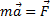

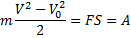

 ;
; 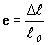
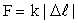 - закон Гука. Сила упругости прямо пропорциональна абсолютной деформации.
- закон Гука. Сила упругости прямо пропорциональна абсолютной деформации.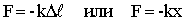 , k - коэффициент жесткости (упругости). Зависит от материала, формы и размеров тела (Например, чем длиннее и тоньше пружина, тем ее жесткость меньше.)
, k - коэффициент жесткости (упругости). Зависит от материала, формы и размеров тела (Например, чем длиннее и тоньше пружина, тем ее жесткость меньше.)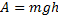


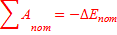



 1). Изохорный процесс (Рис.4.1).
1). Изохорный процесс (Рис.4.1).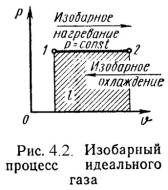 2). Изобарный процесс (Рис.4.2).
2). Изобарный процесс (Рис.4.2).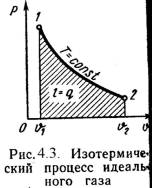 3). Изотермический процесс (Рис.4.3).
3). Изотермический процесс (Рис.4.3). 4). Адиабатный процесс (Рис.4.4).
4). Адиабатный процесс (Рис.4.4).