
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резервирование с постоянно включенном резервомСодержание книги Поиск на нашем сайте Структурная схема системы с постоянно включенным резервом изображена на рис. 10. Элемент с номером 0 является основным, а элементы с номерами 1, 2, …, m – резервными. Общее число элементов в системе n = m + 1, где m – кратность резервирования – отношение числа резервных элементов к числу основных.
В данном случае отказ системы наступает при отказе элемента с максимальным временем работы, т.е.
По теореме умножения вероятностей имеем:
Отсюда следует, что вероятность отказа системы равна произведению вероятностей отказов элементов:
На практике достаточно часто имеют место случаи, когда основная система и все резервные одинаковые и имеют одинаковую вероятность безотказной работы P(t). Тогда
Так как f (t) = Q ’(t), то
Определим интенсивность отказов λc(t) резервированной системы с постоянно включенным резервом. По определению интенсивности отказов имеем:
Резервирование с дробной кратностью Существуют технические системы, часто называемые мажоритарными, с дробной кратностью резервирования Мажоритарная система будет работоспособной в течение времени t (событие А) при отказе не более чем m элементов. Пусть Ai – событие, состоящее в отказе любых i (0 ≤ i ≤ m) элементов за время t. Тогда
Событие Ai произойдет, если откажут любые i элементов, а остальные n-1 элементов останутся работоспособными. Вероятность этого события выражается формулой Бернулли (прил. 7):
Поскольку события Ai попарно несовместимы, то вероятность суммы событий равна сумме вероятностей этих событий, т. е.:
Таким образом, вероятность безотказной работы мажоритарной системы при условии, что все элементы имеют одинаковую надежность, равна:
Найдем интенсивность отказа λс(t) и плотность распределения fc(t) мажоритарной системы. Так как частота отказов есть производная от вероятности безотказной работы,
После преобразования этого выражения получим следующую формулу:
Тогда
Резервирование замещением Структурная схема системы с резервированием замещением представлена на рис. 11. Отказ системы в данном случае наступает после отказа основного элемента и всех резервированных.
Общее время до отказа системы равно сумме времен до отказа элементов
Определим вероятность безотказной работы системы в течение времени t. Примем для начала, что m = 1. Система проработает безотказно в течении времени t при наступлении одного из двух несовместимых условий: - Элемент с номером 0 проработает безотказно в течении времени t; - Элемент с номером 0 откажет в некоторый момент времени x < t, а элемент с номером 1 проработает безотказно в течение оставшегося времени (t - x). Вероятность события A равна P0(t). Вероятность события B, получена по формуле полной вероятности, равна Согласно теореме сложения вероятностей, получим:
Эта формула обобщается на систему, состоящую из произвольного числа элементов:
На практике часто резервирование замещением осуществляется однотипными элементами, когда основной элемент и все резервные равнонадежны. В этом случае формула (14.2) принимает вид:
где
Среднее время безотказной работы можно получить из соотношения
После интегрирования получим:
где T0 – среднее время безотказной работы основного элемента. Скользящее резервирование Скользящим называется резервирование мажоритарной системы m/n с резервом замещением (ненагруженным). Схема такого резервирования представлена на рис. 12.
Рис. 12. Система со скользящим резервированием Сначала работают (n - m) основных элементов системы, а остальные m элементов не работают (находятся в очереди). При отказе любого основного элемента он заменяется новым из числа резервных, который теперь выполняет функции основного элемента. При этом количество резервных элементов уменьшится на единицу. При отказе следующего основного элемента он опять заменяется новым из числа резервных и т.д. Отказ всех системы наступает, когда закончатся все резервные элементы системы и откажет один из основных. Определим вероятность безотказной работы системы со скользящим резервированием при условии, что все элементы системы имеют одинаковую надежность. Система будет работоспособной в течение времени t при отказе не более чем m элементов. Событие Ак, состоящее в отказе любых k (0 ≤ k ≤ m) элементов за время t, может произойти в том случае, когда произойдет хотя бы одно из несовместимых событий Вероятностные характеристики системы со скользящим резервированием не являются темой данного пособия, однако стоит заметить, что скользящее резервирование высокоэффективно. Система, состоящая из n элементов с одним резервным, имеет такую вероятность безотказной работы, как и дублированная система, число элементов которой равно 2(n-1).
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


 .
. (12.1)
(12.1) или
или  (12.2)
(12.2)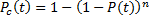 (12.3)
(12.3) (12.4)
(12.4) . (12.5)
. (12.5) , где m – число резервных элементов, n – общее число элементов.
, где m – число резервных элементов, n – общее число элементов.
 .
.
 (13.1)
(13.1)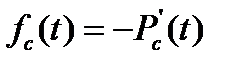 , то используя формулу (13.1) получим:
, то используя формулу (13.1) получим: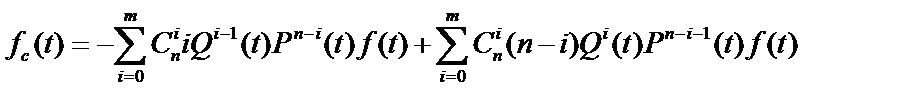 .
. (13.2)
(13.2)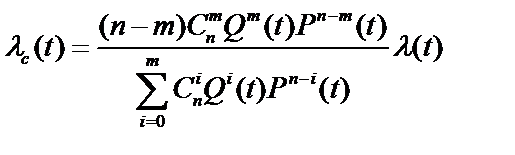 (13.3)
(13.3)
 . Согласно теории вероятностей, плотность суммы независимых случайных величин равна свертке плотностей слагаемых:
. Согласно теории вероятностей, плотность суммы независимых случайных величин равна свертке плотностей слагаемых: (14.1)
(14.1) .
.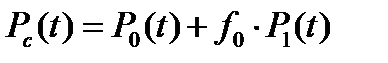
 (14.2)
(14.2) (14.3)
(14.3) – i-кратная свертка плотностей. Преобразуем полученное выражение, исходя из условия, что интенсивность отказов является величиной постоянной, сумма случайных величин из (m + 1)-го слагаемого, каждое из которых имеет экспоненциальное распределение с параметром λ, подчинена распределению Эрланга с параметрами α = m + 1 и β =
– i-кратная свертка плотностей. Преобразуем полученное выражение, исходя из условия, что интенсивность отказов является величиной постоянной, сумма случайных величин из (m + 1)-го слагаемого, каждое из которых имеет экспоненциальное распределение с параметром λ, подчинена распределению Эрланга с параметрами α = m + 1 и β =  . Получаем:
. Получаем: (14.4)
(14.4)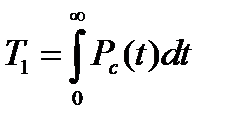 .
. (14.5)
(14.5)
 , которое состоит в том, что основной элемент системы, стоящий на i-ом месте, будет заменен ki резервным элементом, i=1, 2,…,n-m.
, которое состоит в том, что основной элемент системы, стоящий на i-ом месте, будет заменен ki резервным элементом, i=1, 2,…,n-m.


