
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы распределения времени безотказной работыСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
При изучении надежности технических устройств наиболее часто применяются следующие законы: экспоненциальный, нормальный, Релея, Вейбулла-Гнеденко. Рассмотрим наиболее часто используемые в теории надежности семейства распределения случайной величины – параметрические, т. е. зависящие от одного или нескольких параметров. Функция
задает экспоненциальное (или показательное) распределение. Экспоненциальным законом распределения можно аппроксимировать время безотказной работы большого числа элементов. Это относится к элементам радиоэлектронной аппаратуры и машинам, эксплуатируемым в период после окончания приработки и до существенного проявления постепенных отказов. Экспоненциальное распределение применяется в областях, связанных с «временем жизни»: в медицине – продолжительность жизни больных, в надежности – продолжительность безотказной работы устройств, в психологии – время, затраченное на выполнение тестовых задач. Это распределение имеет один параметр
Функция надежности определяет вероятность безотказной работы за время t по следующей формуле:
Интенсивность отказов в данном случае есть величина постоянная. Экспоненциальное распределение выделяется среди других распределений свойством «отсутствия памяти». Пусть Х – время службы некоторого изделия с экспоненциальным законом распределения. «Отсутствие памяти» означает, что изделие, проработавшее время t, имеет такое же распределение, что и новое, только что начавшее работу. Математически это свойство выражается в виде следующего равенства:
для любых t, x ≥ 0. Данное свойство как бы исключает износ и старение изделия. Числовые характеристики экспоненциального распределения выражается через его параметр: математическое ожидание Для характеристики постепенных отказов обычно используют другие законы распределения. Нормальному закону распределения (распределению Гаусса) подчиняются: - время безотказной работы производственных систем, потеря работоспособности которых связана в основном с постепенными отказами, при этом доля внезапных отказов весьма мала; - случайные величины массовых явлений, на которые оказывает влияние большое количество различных по величине факторов (например, износ и усталость деталей, технологические погрешности, точность размеров, получаемых при обработке и т. д.). Нормальному закону распределения подчиняются только непрерывные случайные величины. Поэтому нормальное распределение может быть задано:
и зависит от двух параметров T cp и σ, которые являются соответственно средним временем безотказной работы (математическим ожиданием) и средним квадратическим отклонением времени безотказной работы элемента. Согласно закону больших чисел, распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие примерно равнозначные факторы. Нормальному распределению подчиняются ошибки измерения деталей, дальность полета снарядов и т.п. При большом времени работы элемента и наличии восстановления среднее число отказов имеет асимптотически нормальное распределение. Для нормального распределения функция надежности вычисляется по формуле:
где – Часто в литературе встречается следующая формула функции надежности для нормального распределения:
где Ф 0 – функция Лапласа. По своему логическому содержанию функция Лапласа близка к интегральной функции нормального распределения, их взаимосвязь:
Время безотказной работы, подчиняющееся нормальному закону распределения, имеет следующие свойства: ü одинаковые положительные и отрицательные отклонения от средней арифметической T cp равновозможны; ü меньшие отклонения более вероятны, чем большие; ü весьма большие отклонения от T cp маловероятны; Закон распределения Вейбулла-Гнеденко используется при определении надежности изделий в период приработки и установления наработки на отказ неремонтируемых изделий. Распределение Вейбулла-Гнеденко двухпараметрическое. Его параметрами являются T cp и b – положительные постоянные. Показатели надежности при законе Вейбулла-Гнеденко находятся по следующим формулам: - вероятность безотказной работы
- частота отказов
- интенсивность отказов
- среднее время безотказной работы
где Г (x) – гамма-функция. Следует отметить, что при b = 1 распределение Вейбулла-Гнеденко превращается в экспоненциальное, а при b = 2 – в распределение Релея, при b = 3.3 распределение близко к нормальному. Оно хорошо описывает наработку деталей по усталостным нарушениям, наработку до отказа подшипников, а также используется для оценки надежности деталей и узлов машин, автомобилей. Закон Релея может быть применен при исследовании надежности изделий, имеющих элементы с выраженным эффектом старения: Если случайная величина распределена по закону Релея, то вероятность безотказной работы определяется из уравнения:
где σ – среднеквадратическое отклонение (параметр распределения). Частота отказов (плотность распределения) будет иметь вид:
Интенсивность отказов находится так:
Средняя наработка на отказ (средний ресурс, средний срок службы, среднее время восстановления работоспособного состояния) определяется следующим уравнением:
Следует также отметить, что существуют и другие законы распределения времени до отказа, однако применяются они достаточно редко и рассматриваться нами не будут.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 4643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.71.149 (0.008 с.) |


 , где T 1 – средняя наработка элемента до отказа. Таким образом, параметр λ характеризует число отказов элемента в единицу времени и называется интенсивность отказов. Плотность экспоненциального распределения задается как:
, где T 1 – средняя наработка элемента до отказа. Таким образом, параметр λ характеризует число отказов элемента в единицу времени и называется интенсивность отказов. Плотность экспоненциального распределения задается как: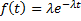 (9.1)
(9.1) (9.2)
(9.2)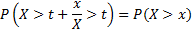
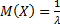 , дисперсия
, дисперсия  , среднее квадратическое отклонение
, среднее квадратическое отклонение 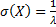 .
. , –∞ < t < +∞ (9.3)
, –∞ < t < +∞ (9.3) (9.4)
(9.4)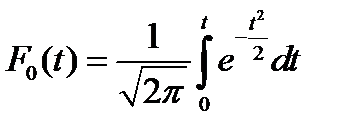 функция нормального распределения, значения которой сведены в таблицы.
функция нормального распределения, значения которой сведены в таблицы. , (9.5)
, (9.5)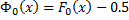
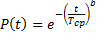 (9.6)
(9.6)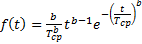 (9.7)
(9.7) (9.8)
(9.8) , (9.9)
, (9.9) , (9.10)
, (9.10)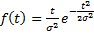 . (9.11)
. (9.11)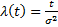 . (9.12)
. (9.12) . (9.13)
. (9.13)


