
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конверсии постоянных аннуитетовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Виды конверсии. В практике иногда сталкиваются со случаями, когда на этапе разработки условий контракта или даже в ходе его выполнения необходимо в силу каких-либо причин изменить условия выплаты аннуитета. Иначе говоря, речь идет о конвертировании условий аннуитета. Простейшими случаями конвертирования являются: замена ренты разовым платежом, иначе говоря, выкуп ренты, или, наоборот, замена разового платежа рентой, т.е. речь идет о рассрочке платежа. К более сложным случаям относятся: объединение рент в одну — консолидация рент, замена ренты с одними условиями на ренту с другими условиями, например немедленной ренты на отложенную, годовой — на ежеквартальную и т.д. Ясно, что все перечисленные изменения не могут быть произвольными. Если предполагается, что конверсия не должна приводить к изменению финансовых последствий для каждой из участвующих сторон, то ее необходимо основывать на принципе финансовой эквивалентности, о котором неоднократно говорилось выше. Конверсия рент широко применяется при реструктурировании задолженности. Как известно, при этом нередко условия погашения долга "смягчаются", однако принцип эквивалентности соблюдается и в этих случаях, правда, в "урезанном" виде. Подробнее о реструктурировании долга будет сказано в гл. 7. Здесь же рассмотрим несколько основных случаев конверсии аннуитетов. Выкуп ренты. В случае замены ренты единовременным платежом решение проблемы очень простое. Искомый размер выкупа должен быть равен современной стоимости выкупаемой ренты. Для решения задачи в зависимости от условий погашения задолженности выбирается та или иная формула расчета современной стоимости потока платежей (см. гл. 4 — 5). Естественно, что применяемая при расчете современной стоимости ставка должна удовлетворять обе участвующие стороны. Рассмотрим одну из ряда возможных постановок задачи. Пусть для конкретности речь идет о продаже долгового обязательства. Имеются три агента: должник, кредитор, покупатель обязательства. Долг согласно договору между должником и кредитором погашается отложенной на два года постоянной годовой рентой постнумерандо. Размер члена ренты равен R, ее срок (без учета отсрочки) равен п. Сумма выкупа определяется в данном случае как A = Ran;iv 2. Как видим, в такой постановке не имеет значения ни ставка, которая применялась при определении R, ни первоначальная сумма долга. Рассрочка платежей. Обсудим теперь задачу, обратную выкупу ренты. Если есть обязательство уплатить некоторую крупную сумму и стороны согласились, что задолженность будет погашена частями — в рассрочку, то последнюю удобно осуществить в виде выплаты постоянной ренты. (П.М. Третьяков, например, предлагал В.В. Верещагину оплатить коллекцию его картин путем выплаты соответствующего аннуитета.) Для решения задачи приравниваем современную стоимость ренты, с помощью которой производится рассрочка, к сумме долга. Задача обычно заключается в определении одного из параметров этой ренты — ее величины или срока выплаты — при условии, что остальные параметры заданы. Подобного рода задачи подробно обсуждались в параграфе 4.4, поэтому здесь нет смысла останавливаться на них. Объединение (консолидация) рент. Объединение рент, очевидно, заключается в замене нескольких рент одной. В этом случае из принципа финансовой эквивалентности следует равенство современных стоимостей заменяющей и заменяемых рент, что соответствуетравенству
Объединяемые ренты могут быть любыми: немедленными и отсроченными, годовыми и р -срочными и т.д. Что касается заменяющей ренты, то следует четко определить ее вид и все параметры, кроме одного. Далее, для получения строгого баланса условий необходимо рассчитать размер неизвестного параметра исходя из равенства (5.27). Этим параметром может быть член ренты или ее срок. Так, если задан срок заменяющей немедленной ренты, то из равенства (5.27) следует:
Если задаются сумма платежа (члена заменяющей ренты) и его периодичность, то отыскивается срок новой ренты (см. параграф 4.4 и табл. 4.1). Обычно задача сводится к расчету n по заданному значению an;i. Последняя величина определяется условиями задачи.
Если
Как видим, для того чтобы задача имела решение, необходимо соблюдать условие: Пример 5.10. Три ренты постнумерандо немедленные, годовые заменяются одной отложенной на три года рентой постнумерандо (см. формулу (4.43)). Заменяющая рента имеет срок n = 10 лет, включая отсрочку. Характеристики заменяемых рент: R = 100; 120; 300, сроки этих рент — шесть, одиннадцать и восемь лет соответственно. Если в расчете принять ставку сложных процентов, равную 20%, то сумма современных стоимостей этих рент составит 2002,946 (см. табл. 5.1). Размер члена заменяющей ренты равен:
Если бы заменяющая рента была немедленной, то
Таблица 5.1 (см. стр 133 (anq; 20 и Rqanq; 20))
Продолжим пример. Пусть теперь заданным является не срок, а сумма годового платежа, скажем 1500, и необходимо найти срок заменяющей ренты. Ход решения: определяется современная стоимость немедленной ренты, затем рассчитывается ее срок после льготного периода: A = 2002,946 х 1,23 = 3461,091. По формуле (4.27) получим:
Округляем ответ до трех или четырех лет и компенсируем нехватку покрытия долга или излишки — см. пояснения в параграфе 4.4 при определении срока ренты. Рассмотрим один частный случай. Пусть член заменяющей ренты равен сумме членов заменяемых рент:
Все ренты Годовые, постнумерандо. Если процентная ставка одинакова у всех рент, то в силу формулы (5.29) получим:
где п — срок заменяющей ренты. После преобразований находим:
Пример 5.11. Консолидируются ренты, предусматривающие Годовые платежи в суммах 0,5, 1,5 и 3; сроки этих рент — 10, 15 и 12 лет, процентная ставка у заменяющей ренты — 5% годовых. В этом случае R = 5 и n = Рассмотренные варианты объединения рент, естественно, не охватывают все возможные случаи, с которыми можно столкнуться на практике. Да в этом и нет необходимости. Отправляясь от равенства современных стоимостей консолидируемых и заменяющей рент, легко вывести соответствующую формулу для решения конкретной задачи. Например, для случаев, когда разные процентные ставки у консолидируемых рент и т.д.
Изменения параметров ренты Изменение хотя бы одного условия ренты по существу означает замену одной ренты другой. Если такая замена базируется на принципе финансовой эквивалентности, то из этого следует равенство современных стоимостей обеих рент (разумеется, при одинаковой процентной ставке, принятой для дисконтирования). Отправляясь от этого равенства, нетрудно определить параметры заменяющей ренты. Рассмотрим несколько случаев такой замены. Замена немедленной ренты на отсроченную. Пусть имеется немедленная рента постнумерандо с параметрами R 1, n 1 Необходимо отсрочить выплаты на t лет. Иначе говоря, немедленная рента заменяется на отсроченную с параметрами R 2, n 2, t (t не входит в срок ренты). Пусть процентная ставка равна i. Здесь возможны разные постановки задачи в зависимости от того, что задано для новой ренты. Если задан срок, то определяется R 2, и наоборот. Рассмотрим первую задачу при условии, что n 2 = n 1 = n. Для этого случая справедливо следующее равенство: A 1 = A 2; R 1 an;i = R 2 an;ivt. Отсюда
Иначе говоря, член новой ренты равен наращенному за время t члену заменяемой ренты. В общем случае, когда n 2
где t — продолжительность отсрочки. Пример 5.12. Пусть немедленная рента постнумерандо с условиями R 1 = 2 млн. руб. и сроком восемь лет откладывается на два года без изменения срока самой ренты, процентная ставка, принятая для пролонгирования, - 20% годовых. Тогда согласно формуле (5.32): R 2 = 2 x 1,22 = 2,88 млн. руб. Если же срок ренты увеличивается, скажем, еще на три года (n = 11), тогда при условии, что i = 20%:
Рассмотрим еще один вариант. Пусть член ренты остается без изменений. Однако выплата ренты откладывается на t лет. Тогда из равенства
находим
Пример 5.13. Рента с условиями R = 2000 тыс. руб., n = 5 лет, i = 8% откладывается на три года без изменения ее члена. Необходимо найти новый срок и сбалансировать результат. По формуле (5.34) получим: n 2 = Примем продолжительность новой ренты (без учета отсрочки) шесть лет. Современная стоимость такой ренты равна: A 2 = Ra 6;8 v 3 = 2000 х 4,6288 х 1,08-3 = 7339,58 тыс. руб. Однако у заменяемой ренты современная стоимость равна 7985,42 тыс. руб. Разность в сумме 645,84 тыс. руб. следует уплатить в начале действия контракта или с соответствующим наращением в любой иной момент. Замена годовой ренты нa p -срочную. Пусть годовая немедленная рента с параметрами R 1, n 1 заменяется нa p -срочную с параметрами R 2, n 2, p. Если заданы срок заменяющей ренты, ее периодичность и ставка, то
Причем, если n 2 = n 1 = n, то
Отсюда
Пример 5.14. Пусть r 1 = 2, n 1 = n 2 = n. Если годовая рента пост-нумерандо заменяется, скажем, на квартальную, то при неизменности срока ренты эквивалентность достигается только за счет корректировки размера выплат. При условии, что i = 20%, находим: R 2 = Продолжим пример. Пусть п 1 = 3, a n 2 = 4 года. Согласно формуле (5.35) получим
Следовательно,
Замена годовой ренты на р -срочную может быть осуществлена и при условии, что заданным является размер члена ренты. Определяется ее срок. В общем случае для этого находим:
Далее по формуле (4.31) определяется n. Общий случай конверсии. Выше методы эквивалентной (безубыточной) замены рент рассматривались применительно к постоянным дискретным рентам. Однако переход от одного вида к другому возможен для любых потоков платежей. В любом случае в основу замены должно быть положено равенство соответствующих современных стоимостей потоков платежей. Ограничимся одним простым примером. Заменим, например, нерегулярный поток постоянной годовой рентой постнумерандо. Пусть поток состоит из платежей R 1, выплачиваемых спустя nt лет после начала действия контракта. Параметры заменяющей ренты: R, п. Исходное равенство имеет вид:
Данное равенство дает возможность определитьодин из параметров ренты — R или n. Решение обратной задачи достигается только подбором величин платежей, удовлетворяющих это равенство. Раздел3 Практические приложения количественного финансового анализа
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 (5.27)
(5.27) (5.28)
(5.28) (5.29)
(5.29) известно, то, решив формулу (5.29) относительно n, находим:
известно, то, решив формулу (5.29) относительно n, находим: (5.30)
(5.30)


 = 3,395 года.
= 3,395 года.

 (5.31)
(5.31) = 12,64 года
= 12,64 года (5. 32)
(5. 32) n 1 из равенства A 1 = A 2 следует:
n 1 из равенства A 1 = A 2 следует: (5. 33)
(5. 33) = 2,55393 млн. руб.
= 2,55393 млн. руб.
 (5.34)
(5.34)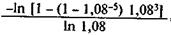 = 6,689 года.
= 6,689 года. (5.35)
(5.35)
 (5.36)
(5.36) = 1,86541.
= 1,86541.

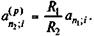 (5.37)
(5.37) (5.38)
(5.38)


