
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доходность потребительского кредитаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Метод начисления процентов в потребительском кредите с равномерным его погашением вовремени рассмотрен в гл. 1. Реальная доходность такого вида ссуды в виде годовой ставки сложных процентов на инвестированные в операцию средствадолжна определяться с учетом фактического остатка задолженности после каждого платежа по кредиту. Погасительные платежи по кредиту представляют собой постоянную р -срочную ренту. Таким образом, оценка искомой ставки сводится к расчету коэффициента приведения такой ренты по данным, характеризующим условия потребительского кредита. Затем на основе полученного коэффициента приведения рассчитывается искомая ставка. Как было установлено в гл. 1, каждый раз должник в счет погашения выплачивает сумму
Годовая сумма платежей равна
Приравняем современную величину платежей (дисконтируя по неизвестной ставке iЭ) сумме долга:
Отсюда
где i — ставка простого процента, принятая при расчетезадолженности по потребительскому кредиту. Значение iЭ рассчитываютпо Таблица 9.1 Доходность потребительского кредита в виде годовой ставки сложных процентов, %
Пример 9.9. Потребительский кредит выдан натри года на сумму 10 млн. руб. по ставке 10% годовых. Общая сумма задолженности составит 10 000(1 + 3 х 0,1) =13 000 тыс. руб. Погасительные платежи образуют постоянную ренту, коэффициент приведения которой
Искомая ставка составит 19,46%. На первый взгляд большой разрыв между номинальной и действительными ставками (10% простых и 19,5% сложных) представляется в какой-то мере парадоксальным. Однако никакого парадокса здесь нет: 10% начисляются на неизменную сумму первоначального долга, в действительности же долг последовательно уменьшается во времени. Потребителя заставляют платить и за кредит, которым он фактически не пользуется. В приведенном примере действительная ставка процентов по потребительскому кредиту почти в два раза превысила объявленную в договоре ставку. Обнаруженное почти двукратное превышение действительной ставки над объявленной ставкой процентов с небольшими вариациями сохраняется, как видно из табл. 9.1, и при других ставках и сроках кредита.
Долгосрочные ссуды Очевидно, что способ погашения долгосрочной задолженности оказывает заметное влияние на эффективность соответствующей финансовой операции для кредитора. В данном параграфе кратко рассмотрены методы оценивания ПД долгосрочных ссуд для двух случаев: 1) когда проценты погашаются последовательными платежами, а основная сумма долга выплачивается в конце срока и 2) когда долг и проценты погашаются последовательно на протяжении всего срока ссуды. В обоих случаях предусматривается выплата комиссионных. Ссуды с периодической выплатой процентов. Если комиссионные не выплачиваются, то доходность равна годовой ставке сложных процентов, эквивалентной любым применяемым в сделке процентным ставкам. Ситуация усложняется, если имеется еще один источник дохода для кредитора — комиссионные. Пусть ссуда D погашается через n лет, проценты по простой процентной ставке i выплачиваются регулярно в конце года. Проценты в таком случае равны Di. Должнику с учетом комиссионных выдается ссуда в размере D (1 - g). Балансовое уравнение, полученное дисконтированием всех платежей по неизвестной ставке iЭ, имеет вид:
Здесь v = (1 + iЭ)-1,
Если проценты выплачиваются р раз в году, то
Задача, следовательно, заключается в нахождениикорня степенной функции. Пример 9.10. На три года выдана ссуда в 1 млн. руб. под 10% годовых,проценты выплачиваются ежегодно. При выдаче ссуды сделана скидка в пользу владельца денег в размере 5%. В результате должник получил 950 тыс. руб. Для расчета искомой ставки iЭ сразу можно написать функцию от iЭ:
Решение, например, методом Ньютона - Рафсона или простым подбором дает iЭ = 1,12088. Таким образом, доходность операции для кредитора и соответственно цена кредита для должника в виде годовой ставки сложныхпроцентов равны 12,088%. По-видимому, здесь уместно произвести проверкурезультата и описать процесс погашения ссуды исходяиз найденного значения процентной ставки. Итак, долг в размере 950 тыс. руб. вырастает за первый год до 950 х 1,12088 = 1064,84, после первой уплаты задолженность составит 964,68; на конец второго года имеем 964,84 х 1,12088 - 100 = 981,47 и, наконец, в последнем году сумма, подлежащая уплате, равна 981,47 х 1,12088 = 1100 тыс., руб. (см. рис. 9.1). Ссуды с периодическими расходами по долгу. Пусть по ссуде периодически выплачиваютсяпроценты и погашается основной долг, причем сумма расходовпостоянна. Тогда балансовое уравнение для случая, когда платежи производятся вконце года, можно представить в виде
где R — ежегодная сумма по обслуживанию долга (срочная уплата). Поскольку
Аналогично для случая, когда погасительные платежи осуществляются р раз в году, находим
где Пример 9.11. Пусть в примере 9.10 задолженность погашается равными платежами. Все остальные условия не изменяются. В этом случае согласно (9.18)
Расчет iЭ по заданному значению iЭ = 12 + Нерегулярный поток платежей. Задолженность может быть погашена путем выплаты нерегулярного потока платежей: R 1,..., Rn. Эффективность кредита при таком способе погашения определим на основе следующего уравнения, балансирующего вложения и отдачи:
где tj — интервал от начала сделки до момента выплаты j -го погасительного платежа. Из условия сбалансированности сделки находим, применяя договорную ставку i, величину последнего взноса:
где q = 1 + iЭ; T = Продемонстрированный выше метод оценки показателя полной доходности на основе функции f (iЭ) применяется, в частности, при анализе облигаций и производственных инвестиций. В следующих главахмы обсудим эти проблемы.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |




 (9.17)
(9.17) одним из приближенных методов, рассмотренных в параграфе 4.4. Получаемая при решении (9.17) относительно iЭ ставкагодовых сложных процентовзаметно больше ставки, примененной при кредитовании (табл. 9.1).
одним из приближенных методов, рассмотренных в параграфе 4.4. Получаемая при решении (9.17) относительно iЭ ставкагодовых сложных процентовзаметно больше ставки, примененной при кредитовании (табл. 9.1).

 . Теперь это уравнение можно представить в виде функции от iЭ следующим образом:
. Теперь это уравнение можно представить в виде функции от iЭ следующим образом: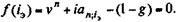



 (см. параграф 7.3), то
(см. параграф 7.3), то (9.18)
(9.18) (9.19)
(9.19) и
и  — коэффициенты приведения годовой и р -срочной ренты, члены которой равны расходам должника по ссуде.
— коэффициенты приведения годовой и р -срочной ренты, члены которой равны расходам должника по ссуде. = a 3;10(l - 0,05) = 2,48685 x 0,95 = 2,36251.
= a 3;10(l - 0,05) = 2,48685 x 0,95 = 2,36251. = 2,36251 можно легко осуществить с помощью линейной интерполяции. Поскольку iЭ > 10%, то примем iн = 12% и iв = 13%. Находим следующие табличные значения коэффициентов приведения: a 3.12 = 2,38134, a 3;13 = 2,36115. Интерполяционное значение ставки
= 2,36251 можно легко осуществить с помощью линейной интерполяции. Поскольку iЭ > 10%, то примем iн = 12% и iв = 13%. Находим следующие табличные значения коэффициентов приведения: a 3.12 = 2,38134, a 3;13 = 2,36115. Интерполяционное значение ставки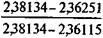 (13 - 12) = 12,933%.
(13 - 12) = 12,933%. (9.20)
(9.20) (9.21)
(9.21)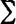 Tj, Tj — срок от выплаты j -го платежа до конца сделки.
Tj, Tj — срок от выплаты j -го платежа до конца сделки.


