
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возмещение премии и накопление дисконта облигацийСодержание книги
Поиск на нашем сайте Проблема оценки облигаций существует не только тогда, когда облигация покупается или продается на рынке, но и когда она находится у владельца. В общем случае ее цена изменяется во времени даже в такой крайне редкой ситуации, когда рыночная процентная ставка остается постоянной, и уж тем более, если эта ставка изменяется. С приближением даты погашения увеличивается современная стоимость суммы, получаемой при погашении облигации, одновременно уменьшается современная стоимость будущих поступлений по купонам. Какой бы ни была цена до погашения, в конце срока цена облигации равна номиналу или некоторой заранее фиксированной выкупной цене. Проследим, к каким изменениям в цене или курсе облигаций приводит ход времени. Для этого вернемся к формуле (11.7) и запишем ее для некоторого момента t после выпуска облигации:
где Kt — курс в момент t (после очередной выплаты процентов); n - t — срок, оставшийся до даты погашения. Для t = n Kt = 100, так как считаем, что проценты в этот момент уже получены. Нетрудно установить, что у облигации, купленной с премией, второе слагаемое курса сокращается скорее, чем увеличивается первое. В связи с этим премия и курс в целом уменьшаются с каждым шагом во времени. Такой процесс получил название возмещение премии (amortization). По определению абсолютный размер премии (дисконта) находится как E = P - N. Премия в расчете на курс в момент t составит et = Kt - 100. На рис. 11.7 и в табл. 11.7 иллюстрируется процесс возмещения премии на примере облигации с условиями: п = 8, g = 8%, i = 6%.
Таблица 11.7
На рис. 11.8 иллюстрируется процесс роста цены за счет накопления дисконта (accumulation). В ходе этого процесса цена и курс облигации увеличиваются во времени, поскольку на каждом шаге во времени рост первого слагаемого перекрывает сокращение второго. Процессы изменения курса рассматривались нами на фоне стабильной рыночной ставки. Однако это условие нереалистично. Действительный курс в связи с изменениями процентной ставки отклоняется от "идеального", динамика которого представлена на рис. 11.7 и 11.8.
Портфель облигаций Портфель (набор), охватывающий различные по видам и срокам облигации, также является объектом количественного финансового анализа. Простейший анализ заключается в оценке полной доходности портфеля и средних, характеризующих сроки платежей. Более сложный — в определении оптимальной структуры портфеля, в разработке и проведении такой стратегии при формировании структуры портфеля, которая обеспечивает гарантированный поток платежей (immunization). Последние из названных направлений анализа требуют самостоятельного рассмотрения, которое выходит за рамки настоящей книги. Доходность портфеля. Данный параметр измеряется в виде годовой ставки сложных процентов. Эта ставка находится с помощью ряда методов. Наиболее точным является решение уравнения, в котором общая стоимость облигаций приравнивается сумме современных величин всех видов платежей.
Величина ∑ QjPj характеризует размер портфеля по цене приобретения, ∑ Stvt — сумма современных величин всех поступлений от облигаций, определенных по искомой ставке i. Здесь St — член потока платежей в момент t; Qj — количество облигаций вида j; pj — цена приобретения облигаций; v — дисконтный множитель по ставке i (напомним, что значение i находят с помощью интерполяции или каким-либо итерационным методом). Приближенные методы заключаются в расчете средних взвешенных ставокпомещения (I).Веса определяются двумя способами. Согласно первому в качестве весов берутся стоимости облигаций по цене приобретения, тогда
Считается, что меньшую погрешность дает взвешивание, когда в качестве весов принимаются произведения показателей D на стоимость облигаций.
Пример 11.16. Портфель, приобретенный за 355 млн. руб., содержит облигации со следующими параметрами:
На основе приведенных данных сформируем поток платежей (табл. 11.8, гр. 2). Для этого найдем размер платежа вконце каждого полугодия. Время в годах здесь: 0,5; 1; 1,5 и т.д. Размер платежа в первом полугодии равен только процентам от облигаций типа В,в конце первого года — сумме процентов по облигациям A и В,в конце четвертого года — сумме процентов и стоимости погашения номинала облигаций типа В. Таблица 11.8
Поскольку ожидаемое значение средней ставки помещения находится между 8 и 9%, рассчитаем соответствующие дисконтные множители — гр. 3 и 4. В гр. 5 и 6 приводятся дисконтированные величины членов потоков платежей. По интерполяционной формуле (11.10), в которой вместо Pk применим сумму цен, находим I = 8 + Проверка: сумма дисконтированных по этой ставке платежей составит 344 850 руб., дальнейшее уточнение оценки дает i = 8,47%, при этом контрольная сумма равна 355 000. Пример 11.17. Найдем приближенные показатели доходности портфеля облигаций примера 11.16. Показателем доходности облигаций в виде годовых ставок сложных процентов равны соответственно 9,3; 6,59 и 9%. Применив приближенную формулу (11.29) (общая стоимость облигаций взята в десятках тыс. руб.), получим I = Ответ заметно отличается от точного (8,47%). Для того чтобы применить формулу 11.30., необходимо найти показатели D для каждого вида облигаций. Определим их по формуле (11.23): 4,2; 8 и 3,47 года. В этом случае для портфеля облигаций получим I = Погрешность в ответе несколько меньше, чем в полученном по формуле (11.29). Средняя продолжительность платежей портфеля. Для дальнейшего анализа портфеля облигаций нам необходимо установить зависимость между общей средней продолжительностью платежей портфеля в целом и аналогичными характеристиками облигаций, входящих в этот портфель. В связи с этим предварительно рассмотрим условный портфель, состоящий из двух облигаций. Соответственно имеются два потока платежей: Rj и Sj. Каждый из данных потоков характеризуется следующими средними продолжительностями платежей:
Для потока платежей от двух облигаций находим
Отсюда следует, что
Таким образом, средняя продолжительность суммарного потока платежей равна средней взвешенной аналогичных характеристик частных потоков. Для m частных потоков получим
где hj — удельный вес цен облигации вида j в сумме цен всех облигации. Удельные веса можно получить на основе не только цен облигаций, но и их курсов. Для облигации k находим
Нетрудно убедиться в том, что найденная выше зависимость справедлива и для модифицированных средних:
Пример 11.18. Найдем для портфеля облигаций примера 11.16 среднюю продолжительность платежей: D 0 = 11.8. Изменение структуры портфеля облигаций. Метод "бабочки" Корректировка структуры портфеля облигаций может преследовать различные цели. Такими целями могут являться повышение доходности уже созданного портфеля или снижение его риска. Реализация таких целей сводится к замене облигаций с одними параметрами на облигации с иными параметрами доходности и риска. Рассмотрим сначала следствия простой замены облигаций в условиях, когда кривая "доходность — риск" положительная (см. рис. 11.9). Напомним, что такая кривая предполагает ускоренное увеличение риска по мере роста доходности. В этих условиях продажа менее доходной облигации A и покупка на эту же сумму более доходной облигации В приведет к повышению доходности соответствующего объема инвестиций на Возможна и обратная ситуация: продажа более доходной облигации и покупка менее доходной, но с заметно меньшим риском. Задачу повышения доходности портфеля облигаций можно решить и более тонким методом: не изменяя величину риска портфеля в целом. Для этого обратимся к методу, который назван его автором "бабочкой"[10]. Суть метода заключается в следующем. Продаются облигации двухвидов: A и С. Первые характеризуются высокой доходностью, вторые — большим сроком. (Выше мы уже говорили о том, что в качестве измерителя риска в финансовой практике часто применяются характеристики срока потока платежей.) Взамен их приобретаются облигации В спромежуточными между облигациями А и В доходностью и сроком (см. рис 11.10). Сформулируем условия такой замены: • стоимость проданных облигаций равна стоимости купленных облигаций; • общий риск портфеля (в виде средней продолжительности платежей D 0 или модифицированной средней MD 0) после замены облигаций не должен измениться.
Задача заключается в определении размеров продажи и покупки каждого вида облигаций. Два сформулированныхвыше условия формализуются следующим образом: VC = VA + VB, (11.32) где VC — рыночная стоимость купленных облигаций С; VA; VB — рыночные стоимости проданных облигаций А и В. В силу доказанного выше свойства — см. формулу (11.31) — получим: VCDC = VADA + VBDB, (11.33) Очевидно, что VA = QADA; VB = QBDB; VC = QCDC, где QA; QB; QC — объемы продаж и покупок облигаций по номиналу; DA; DB; DC — показатели средней продолжительности платежей. Теперь вместо (11.32) и (11.33) получим следующую систему равенств: VC = QAKA + QBKB; VCDC = QAKADA + QBKBDB, где KA; KB; KC — курсы облигаций. Используем эту систему для вывода формул, определяющих суммы продаж и покупки облигаций (заметим, что полученные далее формулы несколько отличаются от формул, предложенных автором. В качестве независимой переменной у него принята величина VC, в полученных нами формулах в качестве таковой выступает QA).Для решения поставленной задачи умножим первое выражение на DB и вычтем из него второе; получим VC (DB - DC) = QAKA(DB - DA). Теперь нетрудно найти рыночную стоимость покупаемых облигаций и их количество (точнее, стоимость по номиналу):
На основе (11.32) получим
Таким образом, задаваясь объемами продажи облигаций вида A, находим размеры продажи и покупки облигаций вида В и С. Решение задачи не может считаться законченным без оценки эффективности операции замены облигаций. Если полная доходность купленных облигаций равна i, а проданных — i', то эффективностьсоставит e = i - i'. Величину i' (средняя доходность облигаций A и В)определим как среднюю взвешенную — см. формулу (11.29); в принятых здесь символахона записывается как
Для того чтобы зависимость эффективности от принятых показателей риска и доходности продаваемых облигаций была более наглядной, преобразуем формулу (11.38), использовав равенство (11.36). После чего находим
где
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.009 с.) |

 t = l, 2,..., n,
t = l, 2,..., n,

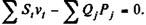
 (11.29)
(11.29) (11.30)
(11.30)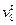



 (9 - 8) = 8,48%.
(9 - 8) = 8,48%. = 8,67%.
= 8,67%. = 8,34%.
= 8,34%.


 j = l, 2,..., m, (11.31)
j = l, 2,..., m, (11.31)
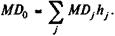
 = 4,43 года.
= 4,43 года. i = iA - iB,авеличины риска — на
i = iA - iB,авеличины риска — на  R = RA - RB. Проблема, очевидно, заключается в определении того, в какой мере полученное отношение приростов
R = RA - RB. Проблема, очевидно, заключается в определении того, в какой мере полученное отношение приростов  удовлетворяетинвестора.
удовлетворяетинвестора.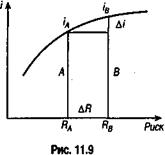

 (11.34)
(11.34) (11.35)
(11.35) (11.36)
(11.36) (11.37)
(11.37)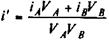 (11.38)
(11.38) ,
, .
.


