Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение эффективности сложных систем. Моделирование инвестиционного процессаСодержание книги
Поиск на нашем сайте
Рассмотренные выше методы измерения эффективности можно получить и для сложных инвестиционных процессов. В этом случае уместно прибегнуть к разработке специальной экономико-математической модели. Основные преимущества использования модели заключаются в одновременном учете в модели большого числа требований, условий и предположений, а также в известной свободе пересмотра этих условий в ходе работы с нею, непротиворечивости (совместности) получаемых по модели системы показателей, возможности получения вариантов поведения изучаемого явления для широкого диапазона и сочетаний исходных условий и предположений (например, вариантов экономического развития, состояния валютно-денежного рынка и т.д.). В настоящей работе мы ограничимся обсуждением проблемы построения моделей для анализа инвестиционного процесса. Особенностью такой модели является то, что в ней, как это было показано в предыдущих параграфах, охватываются два процесса — вложение средств и отдача от них. По существу, полученные выше выражения для оценки показателей эффекта и эффективности представляли собой модели простых инвестиционных процессов. Будем считать сложными такие процессы, в которых последовательность вложений и (или) отдачи состоит Из отдельных участков со специфическими распределениями. Разумеется, и для таких относительно сложных систем можно получить необходимые оценки, последовательно находя соответствующие промежуточные характеристики и обобщая их в виде искомого конечного результата. Однако при таком расчете теряются преимущества модельного подхода, о которых говорилось выше. В частности, модель инвестиционного процесса дает возможность осуществлять так называемый анализ чувствительности (sensitivity analysis). Последний заключается в получении модельных оценок эффекта и эффективности для широкого диапазона возможных условий, в выявлении на этой базе наиболее важных (чувствительных) входных параметров модели. Наконец, анализ чувствительности позволяет выявить закономерности динамики результатов функционирования анализируемой системы в зависимости от изменения каждого из этих параметров. Таким образом, лицу, принимающему решение, предоставляется не единственная оценка эффективности, а развернутая картина (в виде таблиц и графиков) возможных значений эффективности для разнообразных возможных ситуаций. Необходимость в такой аналитической информации определяется прежде всего значительной условностью получаемых оценок эффекта и эффективности, о которой говорилось выше. В свою очередь условность результатов связана с использованием в расчете различных величин, значение которых относится к будущему. Достаточно напомнить, какую роль играет в этих расчетах процентная ставка. Большая условность кроется и в принятых гипотезах о распределении во времени поступлений доходов, издержек производства, ценах и т.д. Анализ чувствительности, не давая окончательно единственной оценки, позволяет установить некоторые ожидаемые интервалы искомых характеристик, тем самым снижается риск неправильного принятия решения. В упомянутом выше обзоре нефтяных компаний США отмечается, что 40% из них применяли анализ чувствительности как средство сокращения риска. Структура инвестиционного процесса. Основная задача при разработке модели, с помощью которой намереваются проанализировать долгосрочный инвестиционный проект, в том числе измерить его финансовую эффективность, сводится к описанию потока поступлений, который следует ожидать при его осуществлении. Первый шаг в этом направлении заключается в разработке структуры этого потока — расчленении на этапы, различающиеся своим содержанием, размерами доходов и затрат. Причем поскольку модель должна давать оценки для различных возможных (ожидаемых) условий величин доходов и затрат, то они в свою очередь должны формироваться в модели в зависимости от внешних условий (например, цен) и производственных параметров (объема производства, уровня затрат). Пусть для большей определенности речь идет о разработке предприятия по добыче каких-либо полезных ископаемых. Тогда процесс осуществления проекта, вероятно, можно расчленить на следующие этапы: изыскание, проектирование, строительство, монтаж и наладка оборудования. В свою очередь процесс отдачи разбивается на период освоения, нормальной эксплуатации, период истощения месторождения. Оба указанных процесса могут быть последовательными или в некоторой своей части совмещаться во времени. Каждый из выделенных интервалов характеризуется специфическим уровнем доходов и расходов — в виде постоянных величин, распределений или в виде зависимостей от каких-либо внешних или производственных условий. Сформированные таким путем последовательности затрат и поступлений дают возможность определить члены потока платежей для каждого момента или отрезка времени и, следовательно, рассчитать показатели эффективности (в первую очередь чистый приведенный доход и внутреннюю норму доходности). Здесь надо обратить внимание на следующее обстоятельство. Как уже отмечалось, подавляющее большинство исходных данных для расчета этих показателей являются оценочными, примерными. Особенно неустойчивыми являются данные об инвестициях в предприятие, в той или иной мере связанное с внешним рынком, экономикой других стран и т.д. Нельзя забывать, коль скоро речь идет о длительных процессах, и о возможности изменения технических параметров, например, при добыче полезных ископаемых, доступе к ним и т.д. Таким образом, зависимость потока поступлений, сформированного в модели, от множества разнообразных данных, относящихся к будущему, не позволяет получить однозначные ответы на все поставленные вопросы. Практически полезным выходом в подобной ситуации является, как известно, сценарный подход. Первоначально получают модельные результаты для некоторого базового сценария, в котором фиксируются наиболее вероятные условия для создания и функционирования производственной системы. Далее аналогичные оценки получают для пессимистичного и оптимистичного вариантов. Совокупность полученных расчетных оценок дает возможность более надежно представить себе финансовые последствия соответствующих инвестиций. Последовательность разработки модели проиллюстрируем на условном примере. Расходная часть проекта охватывает затраты на создание предприятия, эксплуатационные издержки, некоторые периодические выплаты типа ренты, налогов. Доходная часть предусматривает поступления от реализации полученной продукции. Все время создания и функционирования предприятия расчленяется на несколько интервалов, различающихся между собой по величине расходов и доходов. Задача, следовательно, заключается в определении члена потока платежей (затрат и доходов) для каждого такого интервала. Соответствующие величины могут быть постоянными или переменными, дискретными или непрерывными в зависимости от конкретных условий. Например, такие расходы, как изыскания и проектирование, можно рассматривать как постоянные дискретные затраты; строительство, приобретение и монтаж оборудования — как переменные затраты; эксплуатационные расходы — как постоянные и т.д. Что касается доходов, то в каждом из выделенных периодов (освоение, стабильная добыча, истощение месторождения) они могут рассматриваться как непрерывные величины. Причем в первом они систематически растут, во втором — стабильные, в третьем — уменьшаются. Изменение отдачи часто связано с ожидаемым в будущем изменением цен на выпускаемую продукцию. Каждый из отдельных участков потока платежей может быть описан в виде постоянной или переменной ренты. Это дает основание для определения необходимых обобщающих характеристик эффективности инвестиционного процесса в целом. Если поступления или затраты непрерывные и равномерные, то расчет этих характеристик несколько упрощается путем трансформации непрерывного потока в дискретный. Для этого соответствующие суммарные величины относят к середине периодов. Анализ чувствительности модели. О назначении этого анализа говорилось выше. Он состоит из следующих шагов: • выбор основного ключевого показателя, относительно которого и производится оценка чувствительности. В рамках рассматриваемой модели такими показателями могут служить внутренняя норма доходности или чистый приведенный доход; • выбор факторов, влияние которых на ключевые показатели желательно выявить; в первую очередь это параметры, значения которых могут варьировать в относительно широких диапазонах, например ожидаемые цены выпускаемой продукции, динамика производственных затрат, уровень инфляции; • расчет значений ключевого показателя для некоторого диапазона параметров модели. Результаты анализа удобно представить в виде графиков зависимости ключевого параметра от изменения одного из параметров для базового сценария. На рис. 12.7 показана зависимость чистого приведенного дохода W от ожидаемой цены продукта. Области возможных уровней цены (1 - 2) соответствует диапазон а—б показателей чистого приведенного дохода.
Аренда оборудования Частным случаем производственного инвестирования является аренда оборудования. Необходимость в количественном финансовом анализе аренды оборудования возникает как для владельца оборудования, так и для арендатора. Для владельца важно правильное определение размера арендной платы и финансовой эффективности сдачи оборудования в аренду. Арендатор же, если есть альтернатива, должен решить вопрос: арендовать оборудование или купить его? Указанные задачи могут быть решены на основе чисто финансовых принципов, причем любой метод их решения базируется на концепции современной величины денежных потоков. Определение размера платежей за аренду оборудования. Пусть оборудование стоимостью Р сдается в аренду на n лет. Остаточная его стоимость (в конце срока аренды) составит S. Поток арендных платежей с учетом фактора времени должен быть равен сумме износа. Размер разового арендного платежа, обеспечивающего заданный норматив доходности на вложенные в оборудование средства, для случая, когда аренда вносится в конце года, определяется по формуле
где R — размер годовой арендной платы; an;i — коэффициент приведения годовой постоянной ренты; v — дисконтный множитель. Величина арендной платы зависит здесь от стоимости оборудования, принятого норматива доходности i и срока аренды. Формула (12.10) предусматривает арендные платежи один раз в конце года; если условия выплат другие, то применяются коэффициенты приведения соответствующих рент. Величина R характеризует размер арендной платы, обеспечивающей только заданную доходность от сдачи оборудования в аренду. Договор аренды иногда предусматривает ремонт оборудования силами его владельца. За рубежом это обычная практика при сдаче в аренду ЭВМ и других видов сложной техники. Соответствующие издержки учитываются в арендной плате. Учитываемый в расчете норматив доходности, естественно, должен быть больше нормы амортизации оборудования. Разность i - а (где а — норма амортизации) приближенно характеризует реальную доходность арендной операции. Пример 12.9. Оборудование, стоимость которого на момент предоставления в аренду равна 1 млн. руб., сдано на 4 года в аренду. Остаточная стоимость на момент окончания аренды оценивается в 400 тыс. руб. Допустим, что требуемая доходность от вложений в оборудование определена на уровне 15% годовых. Какова должна быть арендная плата, которая обеспечивает заданную доходность при условии, что арендные платежи вносятся: а) один раз в конце года, б) один раз в начале года, в) в начале каждого месяца? Решение получим по формуле (12.10), числитель которой составит 1000 - 400 x 1,15 -4 = 771,3: а) находим а 4;15 = 2,85498, откуда R = Допустим теперь, что срок аренды при всех прочих условиях не 4 года, а, скажем, 8 лет и вдвое уменьшилась остаточная стоимость, тогда a 8;15 = 4,487732 и R = т.е. увеличение срока привело к заметному сокращению годовых арендных платежей; б) a 4;15 x 1,15 = 3,28323 и R = в)
Таким образом, в начале каждого месяца выплачивается 250,26: 12 = 20,855 тыс. руб. Эффективность сдачи оборудования в аренду для владельца. Метод оценки эффективности заключается в расчете уровня доходности в виде годовой ставки сложных процентов. Первым шагом для этого является определение коэффициента приведения ренты по заданным показателям стоимости оборудования, размера арендных платежей и т.д. По найденному значению коэффициента приведения ренты определяется значение годовой процентной ставки i. Для случая, когда арендные платежи выплачиваются один раз в конце года, величина коэффициента приведения находится следующим образом:
где R — сумма арендного платежа без учета расходов на обслуживание и ремонт. Пример 12.10. Пусть арендная плата за оборудование (пример 12.9) установлена в размере 25 тыс. руб., вносимых в начале каждого месяца. Какова действительная эффективность сделки, если норма амортизации равна 10%? По условиям задачи определяем
На основе полученного значения коэффициента приведения ренты интерполяционным методом находим i = 27,8%. При принятой норме амортизации для данного вида оборудования (10%) действительная доходность от сдачи в аренду составляет 17,8%. Арендовать или покупать оборудование? Данная задача представляет собой специальный случай задачи измерения эффективности. Ее решение состоит в сравнении современных величин двух денежных потоков: платежей, связанных с приобретением оборудования, и платежей, определяемых договором аренды. Причем если договор аренды предусматривает ремонт оборудования (и, следовательно, соответствующие затраты включены в арендную плату), то в поток платежей при покупке оборудования для сопоставимости итогов необходимо также включить расходы на ремонт, выполняемый владельцем. Применяемая для дисконтирования ставка процентов должна быть равна рыночной стоимости кредита. Исключение составляет дисконтирование остаточной стоимости оборудования — здесь может применяться другая долгосрочная ставка (норматив рентабельности). Если платежи одинаковы по размеру и производятся через равные промежутки времени, то для определения современных величин потоков платежей следует воспользоваться формулами современных величин соответствующих финансовых рент (см. параграф 4.3). Из условия сравнения следует, что аренда в случае годовых платежей имеет финансовый смысл, если Rап;i < П, где П — современная величина потоков платежей при покупке оборудования. Пример 12.11. Имеется оборудование стоимостью 1 млн. руб., которое может быть предоставлено варенду. Условия аренды: срок — 4 года, ежемесячная арендная плата — 21 тыс. руб., вносится в начале месяца. Условия продажи: цена — 1 млн. руб., аванс — 200 тыс. руб., выплата в начале сделки, на остальную сумму открывается кредит на 5 лет из 6% годовых, погашение задолженности — в конце каждого года. Остаточная стоимость оборудования на конец периода погашения задолженности — 400 тыс. руб. В обоих вариантах ремонт осуществляется за счет пользователей оборудования, поэтому в сопоставительные расчеты эти расходы не включаются. Поток платежей при аренде оборудования состоит из 48 месячных платежей по 21 тыс. руб. Поток платежей при покупке оборудования включает аванс и ежегодные расходы по погашению задолженности. Кроме того, здесь учитывается остаточная стоимость оборудования. Годовая сумма расходов по погашению задолженности при покупке составит
Для дисконтирования соответствующего потока применим ставку, по которой можно разместить средства в данных конкретных условиях. Пусть она равна 8%. Коэффициент приведения ренты в этом случае составит a 5;8 = 3,99271. Тогда современная величина потока платежей определяется как П 1 = 200 + 189,92 х 3,9927 - 400 х 1,08-5 = 686,06 тыс. руб. В свою очередь современная стоимость аренды равна
Таким образом, аренда в этих условиях обойдется намного дороже. Приложение. ТАБЛИЦЫ ДЛЯ ФИНАНСОВЫХ РАСЧЕТОВ
Таблица 2 Множители наращения (сложные проценты)
Таблица 2 (продолжение) Множители наращения (сложные проценты)
Таблица 3 Дисконтные множители (сложные проценты)
|


 (12.10)
(12.10) = 270,16 тыс. руб.
= 270,16 тыс. руб.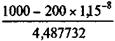 = 208,28 тыс. руб.,
= 208,28 тыс. руб., = 234,92тыс.руб.,
= 234,92тыс.руб., = 3,04631;
= 3,04631; х 1,15 1/12 = 3,08199; R =
х 1,15 1/12 = 3,08199; R =  = 250,26 тыс. руб.
= 250,26 тыс. руб.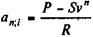 (12.11)
(12.11) (1 + i)l/12 =
(1 + i)l/12 =  = 2,571.
= 2,571.