
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расходы по обслуживанию долгаСодержание книги
Поиск на нашем сайте
Можно выделить по крайней мере три цели для количественного анализа долгосрочной задолженности (далее для краткости любой вид долгосрочного долга будем называть займом или долгом): • разработку плана погашения займа, адекватного принятым условиям финансового соглашения; • оценку стоимости долга на любой момент с учетом всех поступлений для его погашения и состояния денежного рынка на момент оценивания; • анализ эффективности (доходности) финансовой операции для кредитора. Основное внимание в данной и следующей главах уделяется первой из поставленных задач. Остальные проблемы, в том числе связанные с облигационными займами, обсуждаются в последующих главах. Разработка плана погашения займа заключается в составлении графика (расписания) периодических платежей должника. Такие расходы должника обычно называют расходы по обслуживанию долга (debt service), или, более кратко, срочные уплаты, расходы по займу. Расходы по обслуживанию долга включают как текущие процентные платежи, так и средства, предназначенные для погашения основного долга. Методы определения размера срочных уплат существенно зависят от условий погашения долга, которые предусматривают: срок займа, продолжительность льготного периода (grace period), уровень и вид процентной ставки, методы уплаты процентов и способы погашения основной суммы долга. В долгосрочных займах проценты обычно выплачиваются на протяжении всего срока займа. Значительно реже они начисляются и присоединяются к основной сумме долга. Основная сумма долга иногда погашается одним платежом, чаще она выплачивается частями, в рассрочку. В льготном периоде, который часто предусматривается условиями займа, основной долг не погашается, но выплачиваются проценты. Впрочем, не исключается возможность присоединения процентов к сумме основного долга. Каждый из рассмотренных ниже методов планирования погашения долга в той или иной степени, но обязательно использует результаты, полученные выше при анализе финансовых рент. При определении срочных уплат используем следующие основные обозначения: D — сумма задолженности; Y— срочная уплата; I — проценты по займу; R — расходы по погашению основного долга; g — ставка процента по займу;
n — общий срок займа; L — продолжительность льготного периода. По определению срочная уплата находится как Y = I + R. Если в льготном периоде периодически выплачиваются проценты, то в этом периоде Y = I.
7.2.Планирование погасительного фонда Если по условиям займа должник обязуется вернуть сумму долга в конце срока в виде разового платежа, то он должен предпринять меры для обеспечения этого.При значительной сумме долга обычная мера заключается в создании погасительного фонда (sinking fund).Необходимость формирования такого фонда иногда оговаривается в договоре выдачи займа в качестве гарантии его погашения. Разумеется, создание фонда необязательно надо связывать с погашением долга. В практике возникает необходимость накопления средств в заданном размере и по другим причинам, например для накопления амортизационных отчислений на замену изношенного оборудования и т.п. Погасительный фонд создается из последовательных взносов должника (например, на специальный счет в банке), на которые начисляются проценты. Таким образом, должник имеет возможность последовательно инвестировать средства для погашения долга. Очевидно, что сумма взносов в фонд вместе с начисленными процентами, накопленная в погасительном фонде к концу срока долга, должна быть равна его сумме. Взносы могут быть как постоянными, так и переменными во времени. Постоянные взносы в фонд. Как было сказано выше, задача разработки способа погашения долга, в том числе и в виде плана создания погасительного фонда, заключается в определении размеров срочных уплат и составляющих их элементов в зависимости от конкретных условий займа. Итак, пусть накопление производится путем регулярных ежегодных взносов R, на которые начисляются сложные проценты по ставке i. Одновременно происходит выплата процентов за долг по ставке g. В этом случае срочная уплата составит: Y = D g + R. (7.1) Обе составляющие постоянны во времени. Как видим, первая определяется величиной долга и процентной ставкой. Найдем вторую составляющую. Поскольку фонд должен быть накоплен за N лет, соответствующие взносы образуют постоянную ренту с параметрами: R, N, i. Допустим, что речь идет о ренте постнумерандо. Так как накопленная сумма (наращенная сумма ренты) должна быть равна D, то
Y = Dg + D/sN;i, (7.2) т.е. в фонд систематически вносится сумма, равная R = D/sN;i. Если условия контракта предусматривают присоединение процентов к сумме основного долга, то срочная уплата определяется следующим образом:
Пример 7.1. Долг в сумме 100 млн. руб. выдан на пять лет под 20% годовых. Для его погашения создается погасительный фонд. На инвестируемые в нем средства начисляются проценты по ставке 22%. Необходимо найти размеры срочных уплат. Пусть фонд формируется пять лет, взносы производятся в конце каждого года равными суммами. Таким образом, D = 100, N = 5, g = 20%, i = 22%. Находим s 5;22 = 7,7395826 и, следовательно, Y = 100 х 0,2 + Пусть условия контракта предусматривают присоединение процентов к основной сумме долга, тогда согласно формуле (7.3) Y = При создании погасительного фонда, как это было показано выше, используются две процентные ставки — i и g. Первая определяет темп роста погасительного фонда, вторая — сумму выплачиваемых за заем процентов. Нетрудно догадаться, что рассматриваемый способ погашения долга — создание фонда — выгоден должнику только тогда, когда i > g, так как в этом случае должник на аккумулируемые в погасительном фонде средства получает больше процентов, чем сам выплачивает за заем. Чем больше разность i - g, тем, очевидно, больше экономия средств должника, направляемая на покрытие долга. В случае, когда i = g, преимущества создания фонда пропадают. Финансовые результаты для должника оказываются такими же, как и при погашении долга частями. Накопленные за t лет средства фонда определяются по знакомым нам формулам наращенных сумм постоянных рент или рекуррентно: St +1 = St (1 + i) + R. (7.4) Пример 7.2. Продолжим пример 7.1. Пусть средства в фонд вносятся только последние четыре года, остальные условия сохраняются. Тогда R = План формирования такого фонда (в тыс. руб.) представлен в табл. 7.1. Таблица 7.1
Формулы (7.2) и (7.3) получены для ежегодных взносов в фонд и начислений процентов. Если это не так, то применяются соответствующие методы расчета процентов и сумм взносов в фонд. Пример 7.3. Внесем еще одно изменение в условия примера 7.1. Пусть взносы вносятся не ежегодно, а в конце каждого месяца, т.е. р = 12. Проценты выплачиваются кредитору ежегодно. Коэффициент наращения в этом случае равен R = Изменяющиеся взносы. Равные взносы в фонд — простое, но далеко не единственное решение проблемы накопления необходимой суммы денег. В зависимости от конкретных условий могут оказаться предпочтительными изменяющиеся во времени суммы взносов. В таких случаях следует воспользоваться результатами, полученными для переменных рент, — см. гл. 5. Допустим, что взносыв фонд следуют арифметической прогрессии. Очевидно, что срочные уплаты в рассматриваемых условиях изменяются во времени: Yt = Dg + Rt, где Rt = R + a (t - 1), t = 1,..., N. (страница 163. ПРОВЕРИТЬ ЛОГИКУ) Разность прогрессии равна а, первый член — R. Наращенная сумма такой ренты определяется формулой (5.3). Запишем ее в преобразованном виде:
Поскольку наращенная сумма должна быть равна долгу, то заменим в этой формуле S на D. Решив ее относительно R, находим:
Пример 7.4. В фонд погашения долга средства поступают в виде ежегодной ренты постнумерандо в течение пяти лет (срок погашения долга). Платежи каждый раз увеличиваются на 500 тыс. руб. Пусть размер долга на момент его погашения равен 10 млн. руб., на взносы начисляются проценты по ставке 10% годовых. Для разработки плана создания фонда определим величину первого взноса. Предварительно находим s 5;10 = 6,1051. R = Отсюда Rt = 731,91 + 500(t - 1); t = l, 2,..., 5. Динамика расходов должника при условии, что по условиям займа кредитору выплачивается 9,5%, показана в табл. 7.2. В ней в отличие от табл. 7.1 в последней графе показаны суммарные накопления, которые определены по рекуррентной формуле (7.4). Таблица 7.2
Если взносы в данном примере представляют собой убывающую арифметическую прогрессию, допустим, что а = -500, то первый взнос составит R = Перейдем теперь к взносам, изменяющимся в геометрической прогрессии. Наращенная сумма в этом случае определяется по формуле (5.16). Приняв S = D, п = N, находим:
Где R — первый член ренты; q — знаменатель прогрессии. Срочные уплаты составят: Yt = Dg + Rqt- 1. (7.7) Пример 7.5. Пусть долг равен 10 млн. руб., процентные платежи по ставке - 10%, срок погашения - пять лет. Предполагается, что платежи в фонд будут расти на 12% ежегодно. Найдем размер первого взноса при условии, что на взносы начисляются проценты по ставке 9% годовых.По условиям задачи D = 10 000, n = 5, q = 1,2, i = 0,09, g = 0,1. На основе формулы (7.6) находим: R = 10 000 Процесс формирования фонда представлен в табл. 7.3. Таблица 7.3
Разумеется, для накопления фонда в зависимости от обстоятельств можно применить и другие подходы к распределению взносов во времени. Погашение долга в рассрочку В практической финансовой деятельности, особенно при значительных размерах задолженности, долг обычно погашается в рассрочку, частями. Такой метод погашения часто называют амортизацией долга. Он осуществляется различными способами:
• погашение основного долга равными суммами (равными долями); • погашение всей задолженности равными или переменными суммами по обслуживанию долга (срочными уплатами). Погашение основного долга равными суммами. Пусть долг в сумме D погашается в течение п лет. В этом случае сумма, ежегодно идущая на его погашение, составит
Размер долга, как видим, последовательно сокращается: D, D - d, D - 2 d и т.д. Соответствующим образом уменьшаются и выплачиваемые проценты, так как они начисляются на остаток долга. Пусть для простоты проценты выплачиваются один раз в конце года по ставке g. Тогда за первый год и последующие годы они равны Dg, (D — d) g,(D — 2 d) g и т.д. Процентные платежи, как видим, образуют убывающую арифметическую прогрессию с первым членом Dg и разностью -dg. Срочная уплата в конце первого года находится как Y 1 = D 0 g + d. Для конца года t находим: Yt = Dt - 1 g + d; t = l, 2,..., n, (7.8) где Dt — остаток долга на конец года t, D 0= D.
Если долг погашается р раз в году постнумерандо и с такой же частотой выплачиваются проценты, каждый раз по ставке g/p, то срочная уплата составит:
Остаток задолженности на конец года t:
Пример 7.6. Долг в сумме 1000 тыс. руб. необходимо погасить последовательными равными суммами за пять лет платежами постнумерандо. За заем выплачиваются проценты по ставке 10% годовых. Размер погашения основного долга 1000: 5 = 200 тыс. руб. в год. Ежегодные процентные платежи составят 1000 х 0,1 = = 100; (1000 - 200) х 0,1 = 80 и т.д. План погашения представлен в табл. 7.4. Таблица 7.4
Как видим, со временем уменьшаются не только суммы расходов по займу, но и соотношения процентов и сумм погашения основного долга. Условия займа могут предусматривать льготный период, в течение которого основной долг не погашается, проценты выплачиваются или присоединяются к сумме долга. В последнем случае долг увеличивается в конце льготного периода до D 0(1 + g) L. У рассмотренного метода амортизации задолженности есть одно положительное свойство — простота расчетов. Однако, как мы только что убедились, срочные уплаты здесь в начале срока погашения выше, чем в конце этого срока, что часто является нежелательным для должника. Погашение долга равными срочными уплатами. В соответствии с этим методом расходы должника по обслуживанию долга постоянны на протяжении всего срока его погашения. Из общей суммы расходов должника часть выделяется на уплату процентов, остаток идет на погашение основного долга. Так же как и при предыдущем методе, величина долга здесьпоследовательно сокращается, в связи с этим уменьшаются процентные платежи и увеличиваются платежи по погашению основного долга. По определению Y = Dt - 1 g + Rt = const. План погашения обычно разрабатывается при условии, что задается срок погашения долга. Альтернативным и более редким является установление фиксированной суммы постоянных срочных уплат. Рассмотрим оба случая.
Задан срок погашения. Первый этап разработки плана погашения — определение размера срочной уплаты. Далее эта величина разбивается на процентные платежи и сумму, идущую на погашение долга. После этого легко найти остаток задолженности. Периодическая выплата постоянной суммы Y равнозначна ренте с заданными параметрами. Приравняв сумму долга к современной величине этой ренты, находим
где an ; g — коэффициент приведения годовой ренты со ставкой процента g и сроком п. Все величины, необходимые для разработки плана, можно найти на основе Y и данных контракта. Найдем сумму первого погасительного платежа. По определению d 1 = y - d 0 g. Суммы, идущие на погашение долга, увеличиваются во времени: dt = dt- 1(1 + g). (7.11) В связи с этим рассматриваемый метод погашения называют прогрессивным. Платежи по погашению долга образуют ряд: d 1; d 1(l + g);...; d 1(l + g) n - 1. Использовав этот ряд, легко определить сумму погашенной задолженности на конец года t (после очередной выплаты):
где st;g — коэффициент наращения постоянной рентыпостнумерандо. Пример 7.7. Условия погашения займа те же, что и в примере 7.6. Однако погашение производится равными срочными уплатами, т.е. рентой с параметрами: Y (неизвестная величина), n = 5, g = 10%. Находим a 5;10 = 3,790787, после чего Y = d 1 = 263,797 - 1000 х 0,1 = 163,797 тыс. руб.; D 1 = 1000 - 163,797 = 836,203 тыс.руб. План погашения долга представлен в табл. 7.5. Таблица 7.5
Процентные платежи уменьшаются во времени, а суммы погашения основного долга увеличиваются. Пример 7.8. Допустим, что необходимо найти сумму погашенного долга на конец третьего года погашения для данных примера 7.7 при условии, что план погашения не разработан. Для решения воспользуемся формулой (7.12). Находим s 3;10 = 3,31; сумма первого платежа определена выше: d 1 = 163,794, таким образом, W 3= 163,794 х 3,31 = 542,168 тыс. руб. Аналогичным образом разрабатываются планы погашения и для случаев, когда выплата процентов и погашение основного долга производятся не один, а несколько раз в год. Заданы расходы по обслуживанию долга. Такая постановка задачи может возникнуть при разработке условий контракта. Ее решение, очевидно, заключается в определении срока погашения долга и корректировании первичных условий для достижения полной сбалансированности платежей. Срок погашения находится как срок постоянной ренты. Эта проблема подробно обсуждалась в гл. 4 — см. формулы (4. 26) - (4. 35). Пусть выплаты производятся раз в год постнумерандо, тогда применим формулу (4. 27), где символ R заменен на Y:
Очевидно, что решение существует тогда, когда D 0 g / Y < 1. Расчетное значение n в общем случае оказывается дробным. Поэтому его округляют до наименьшего целого числа. Однако при этом план не будет сбалансированным. Напомним, что далее имеются две возможности: найти новое значение Y или компенсировать остаток долга. Пример 7.9. Долг равен 1000 тыс. руб. и выдан под 10% годовых. Для погашения долга предполагается выделять сумму порядка 200 тыс. руб. в год. Оценим величину срока, необходимого для погашения задолженности: n = Округлим расчетный срок до семи лет. Для того чтобы полностью рассчитаться за долг, необходимо несколько повысить срочные уплаты, а именно: Y = Альтернативой является адекватная компенсация недостающего покрытия долга при выплате ренты с членом 200 тыс. руб. и сроком семь лет. Если погасительные платежи и начисленные проценты выплачиваются р раз в году, то расчетное число периодов определяется по формуле
где g — годовая ставка процента. Переменные расходы по займу. Далеко не всегда оказывается удобным условие Y = const. Например, погашение долга может быть связано с поступлением средств из каких-либо источников и зависеть от ряда обстоятельств. Срочные уплаты в этом случае образуют ряд, члены которого либо задаются заранее (график погашения), либо следуют какому-либо формальному закону (прогрессии, заданной функции). Остановимся на одном варианте — изменении расходов в геометрической прогрессии. Итак, пусть ряд срочных уплат представляет собой геометрическую прогрессию со знаменателем q, тогда этот ряд можно записать в виде членов переменной ренты Y, Yq, Yq 2,..., Yqn - 1. Приравняв современную стоимость этой ренты к сумме первоначального долга, находим[7]:
где q — заданный годовой темп роста платежей; g — процентная ставка по займу. Далее рассчитываются срочные уплаты и разрабатывается детальный план погашения. Пример 7.10. Пусть расходы по займу уменьшаются каждый год на 10%; общий срок погашения — пять лет; первоначальная сумма долга - 1000 тыс. руб.; ставка процента по долгу - 6%. По условиям задачи: D 0 = 1000, п = 5, g = 0,06, q = 0,9. Согласно (7.15) первая срочная уплата составит: Y = Процентные платежи в первом периоде 1000 х 0,06 = 60 тыс. руб., соответственно сумма погашения долга равна 286,353 - 60 = = 226,353 тыс. руб., остаток задолженности на начало второго года составляет 1000 - 226,353 = 773,647 тыс. руб. Срочные уплаты находятся как Y x 0,9 t - 1. План погашения долга представлен в табл. 7.6. Таблица 7.6
В ряде случаев размеры срочной уплаты связываются с ожидаемыми поступлениями средств и задаются заранее в виде Графика погашения. Размер последней срочной уплаты не задается. Она определяется как сумма остатка долга на начало последнего периода. Схема расчета показателей плана погашения приведена в табл. 7.7, предполагается, что платежи производятся ежегодно постнумерандо. Таблица 7.7
Льготные займы и кредиты Грант-элемент. Предмет обсуждения в данном параграфе также связан с долгосрочными займами. Однако здесь они рассматриваются под другим углом зрения. Дело в том, что в ряде случаев долгосрочные займы и кредиты выдаются по тем или иным причинам под льготные для заемщика условия. Низкая (относительно ставки на рынке кредитов) процентная ставка в сочетании с большим его сроком и льготным периодом дают должнику существенную выгоду, которую можно рассматривать как субсидию. Кредитор в этих условиях несет некоторые потери, так как он мог бы инвестировать деньги на более выгодных условиях. Проблема определения размера этой помощи обсуждалась в международных организациях и экономической литературе главным образом с позиции межстрановых сопоставлений — для сравнения размеров финансовой помощи, оказываемой ряду развивающихся стран. Однако проблема оценки последствий выдачи льготных займов имеет более общее значение, поскольку такие займы предоставляют и внутри страны. Сама проблема сводится к оценке грант-элемента. Грант-элемент — это условная потеря заимодавца, которая связана с применением более низкой процентной ставки, чем ставка кредитного рынка. Грант-элемент определяется в двух видах: абсолютной и относительной величины. Абсолютный грант-элемент рассчитывается как разность номинальной суммы займа и современной величины платежей по погашению займов. Проблема, как видим, сводится к выбору надлежащей ставки процента для расчета современной величины платежей. Рекомендации по выбору конкретного значения этой ставки весьма расплывчаты, обычно используют превалирующую на рынке долгосрочных кредитов ставку. Размер абсолютного грант-элемента находим следующим образом: W = D - G. (7.16) Относительный грант-элемент:
где W — абсолютный грант-элемент; D — сумма займа; G — современная величина платежей, поступающих в счет погашения займа, рассчитанная по реальной ставке кредитного рынка; w — относительный грант-элемент. Все переменные приведенных формул определяются условиями выдачи и погашения займа. Выведем рабочие формулы для расчета W и w при условии, что долг и проценты выплачиваются в виде постоянных срочных уплат. Для анализа последствий выдачи льготных займов этого достаточно. Пусть заем выдан на n лет и предусматривает выплату процентов по ставке g. На денежном рынке аналогичные по сроку и величине займы выдаются по ставке i. В этом случае срочная уплата составит:
а современная величина всех выплат должника равна Yan ; i. В итоге согласно формуле (7.16):
где an;i, an;g — коэффициенты приведения постоянных годовых рент постнумерандо, определенные для процентныхставок i и g, i > g. Очевидно, что наличие льготного периода увеличивает грант-элемент. Если в льготном периоде должник выплачивает проценты, то современная величина поступлений по долгу определяется как сумма двух элементов — современной величины процентных платежей в льготном периоде и современной величины срочных уплат в оставшееся время. Таким образом, G = Dg x aL;i + Y х аn - L;l x vL, где Y находится по формуле (7.18), L — продолжительность льготного периода. После ряда преобразований получим:
где an - L;i; an - L ; g — коэффициенты приведения постоянных рент со сроком n - L и ставками i и g; vL — дисконтный множитель по ставке i. Обсудим еще один возможныйвариант. Пусть в льготном периоде проценты начисляются, но не выплачиваются. Они присоединяются к основному долгу, который погашается в течение п - L лет. Условия такого займа более льготны для должника, чем при последовательной выплате процентов. Срочные уплаты и их современная величина в данном случае равны:
Пример 7.12. Льготный заем выдан на 10 лет под 3,8%. Предусматривается погашение долга равными срочными уплатами. Известно, что обычная рыночная ставка для такого срока займа равна 8%. В этом случае w = l - Допустим, что исходная сумма займа равна 10 млн. руб. Тогда абсолютный грант-элемент, или условная сумма потерь для кредитора и соответственно выгода для должника, составит: W = 10 х 0,1809 = 1,809 млн. руб. На основе этих выражений получим: w = 1 - Пример 7.13. Пусть заем примера 7.12 предусматривает трехлетний льготный период, в течение которого выплачиваются проценты. Для расчета относительного грант-элемента по формуле (7.21) находим: a 7;8 = 5,20637, а 7;3,8= 6,04667, a 3;8 = 2,5771, v 3 = 1,08-3 = 0,79383. w = 1 - ( Если проценты в льготном периоде не выплачиваются, а присоединяются к основной сумме долга, то w = 1 - Грант-элемент, как было продемонстрировано выше, — условная обобщающая характеристика льготности займа (потерь заимодавца и выигрыша должника). Сумма, которая равна грант-элементу, существенно зависит от принятой при ее определении процентной ставки. График зависимости относительных потерь от соотношения процентных ставок показан на рис. 7.1 для сроков займа пять и десять лет без льготного срока, g = 5%.
Беспроцентный заем. Предельным случаем льготного займа является беспроцентный заем. Выдача такого займа связана с потерями, которые определим, полагая, что соответствующие средства можно было бы разместить под проценты по рыночной ставке i. Условия беспроцентного займа могут предусматривать льготный период, в течение которого погасительные платежи не поступают (отсрочка погашения). Пусть долг погашается равномерно, каждый год в сумме D/n постнумерандо. Современная величина погасительных платежей равна
Относительная величина потерь, которую также можно назвать относительным грант-элементом, находится как
Наличие отсрочки, естественно, увеличивает потери для кредитора:
Пример 7.14. Беспроцентный заем предоставлен на десять лет. Допустим, что на кредитном рынке средний размер ставки для такого срока составляет 10%. Для указанных условий находим w = 1 - Выдача такого займа равнозначна субсидии, равной 38,55% суммы займа. Если предусматривается трехлетний период отсрочки, то w = l - Значения относительных потерь в процентах для некоторых сроков беспроцентных займов без отсрочки и ряда уровней рыночных процентных ставок приведены в табл. 7.9. Таблица 7.9
Как следует из таблицы, уже при пятнадцатилетнем сроке и ставке в 10% кредитор теряет почти 50% суммы долга.
Реструктурирование займа Под реструктурированием займа (restructuring loan, renegotiating loan) понимают пересмотр условий действующего обязательства по погашению задолженности в связи с резким ухудшением финансового положения должника (лучше потерять кое-что, чем все). При реструктурировании применяются разные приемы, основными из которых являются: • прямое сокращение суммы долга; • уменьшение размера процентной ставки; • пересмотр сроков и порядка выплат процентов и сумм погашения основного долга. На практике одновременно может быть применено несколько из указанных способов. Например, известны такие случаи, когда к одной части обязательства применяли сокращение суммы основного долга, к другой — снижение процентной ставки. Какой бы способ реструктурирования не был принят, следствием является уменьшение современной стоимости выплат. Поэтому выбор варианта реструктурирования заключается в сравнении соответствующих оценок. В качестве иллюстрации кратко рассмотрим два из пяти предложенных вариантов реструктурирования долгосрочной задолженности Польши западным кредиторам[8]. Первый вариант: погашение основной суммы долга разовым платежом через 30 лет, переменные ставки — от 2,75 в первом году до 5% годовых в последнее десятилетие. Второй вариант: льготный период равен 20 годам, погашение основной суммы долга осуществляется в последние пять лет, выплаты производятся по полугодиям равными суммами (11 платежей), выплата процентов — от 4,5 в первом году до 7,5% в последние 15 лет (выплата процентов по полугодиям). Если современные стоимости рассчитывать при условии, что процентная ставка, принятая для дисконтирования, равна 12%, то для первого варианта современная стоимость выплат по долгу равна 31%, для второго — 53% величины долга.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1675; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.89.70 (0.012 с.) |

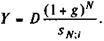 (7.3)
(7.3)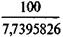 = 20 + 12,92059 = 32,92059 млн. руб.
= 20 + 12,92059 = 32,92059 млн. руб. = 32,15056 млн. руб.
= 32,15056 млн. руб.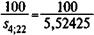 = 18,10201 млн. руб.
= 18,10201 млн. руб.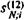 — см. формулу (4.12). Годовая сумма взносов в фонд составит:
— см. формулу (4.12). Годовая сумма взносов в фонд составит: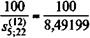 = 11,7758 млн. руб.
= 11,7758 млн. руб.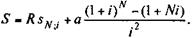
 (7.5)
(7.5)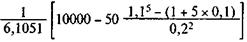 = 732,91 тыс. руб.
= 732,91 тыс. руб.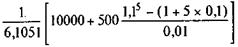 = 2543,04 тыс. руб.
= 2543,04 тыс. руб.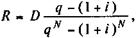 (7.6)
(7.6) = 1317,248 тыс. руб.
= 1317,248 тыс. руб.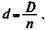

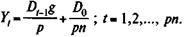 (7.9)
(7.9)
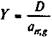 (7.10)
(7.10) (7.12)
(7.12) = 263,797 тыс. руб.;
= 263,797 тыс. руб.;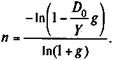 (7.13)
(7.13)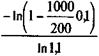 = 7,2725 года.
= 7,2725 года.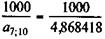 = 205,405 тыс. руб.
= 205,405 тыс. руб.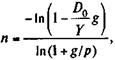 (7.14)
(7.14)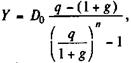 (7.15)
(7.15)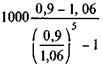 = 286,353 тыс. руб.
= 286,353 тыс. руб.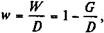 (7.17)
(7.17)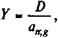 (7.18)
(7.18)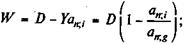 (7.19)
(7.19)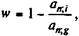 (7.20)
(7.20)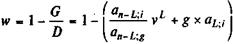 , (7.21)
, (7.21)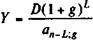 ; G = Y x an_L;i.
; G = Y x an_L;i.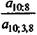 = 1 - 6,71008 х
= 1 - 6,71008 х 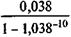 = 0,1809.
= 0,1809.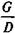 = 1 -
= 1 - 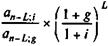 .
.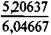 0,74383 + 0, 038 х 2,5771) = 0,2185.
0,74383 + 0, 038 х 2,5771) = 0,2185. = 0,2356.
= 0,2356.
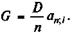
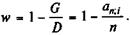 (7. 22)
(7. 22) (7. 23)
(7. 23)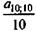 = 1 -
= 1 - 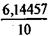 = 0,3855.
= 0,3855. 1,1-3 = 0,47732.
1,1-3 = 0,47732.


