
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постоянная непрерывная рентаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Во всех рассмотренных выше рентахпредполагалось, что члены потока платежейпоступают дискретно — через фиксированные интервалы времени (периоды ренты). Вместе с тем иногда более адекватное описание потока платежей достигается, когда он воспринимается как непрерывный процесс. Например, когда отдача от инвестиций происходит так часто, что в целом этот поток можно рассматривать как непрерывный. Предположение о непрерывности в определенных условиях увеличивает возможности количественного анализа, особенно при сложных производственных долгосрочных инвестиций. Обсудим методы расчета наращенной суммы и современной стоимости, а также ряд параметров, характеризующих постоянную непрерывную ренту при условии, что применяется годовая дискретная процентная ставка. По определению у непрерывной ренты
Непосредственная подстановка
Раскроем неопределенность, применив правило Лопиталя, получим
Таким образом,
Аналогичным путем получим коэффициент наращения непрерывной ренты:
Очевидно, что переход от дискретных взносов постнумерандо к непрерывным увеличивает соответствующие коэффициенты в i/ ln (1 + i) раз.
Пример 4.22. Ожидается, что доходы от эксплуатации месторождения полезных ископаемых составят 1 млрд. руб. в год, продолжительность разработки — 10 лет, отгрузка и реализация продукции непрерывны и равномерны. Капитализированная стоимость дохода при дисконтировании по ставке 10% составит:
Заметим, что формулы (4.46) и (4.47) предполагают непрерывное поступление платежей и дискретное начисление процентов. Вероятно, более "естественным" является положение, когда оба процесса непрерывны. Для получения формул соответствующих коэффициентов воспользуемся формулами эквивалентности между непрерывными и дискретными ставками:
Формулы (4.46) — (4.49) дают одинаковые результаты только в том случае, когда непрерывные и дискретные ставки являются эквивалентными (см. параграф 3.3). Пример 4.23. Пусть в примере 4.22 дисконтирование осуществляется по силе роста 10%, тогда согласно формуле (4.48)
Эквивалентная дискретной ставке 10% (которая была применена в примере 4.22) сила роста составит
Формулы (4.48) и (4.49) можно получить и с помощью интегрирования. Например, коэффициент приведения находим следующим образом:
Остановимся теперь на одном частном, но практически важном вопросе. Определим величину коэффициента наращения непрерывной ренты для годового интервала времени. Обозначим коэффициент наращения p -срочной ренты для этого интервала как
Разложим эту функцию в степенной ряд, ограничившись первыми тремя членами:
Близкий к этому результат дают и первые три члена разложения бинома (1 + i)l/2.
В итоге
Иначе говоря, равномерная и непрерывная выплата годовой суммы P примерно равнозначна разовой выплате этой суммы в середине года. Аналогично находим коэффициент приведения непрерывной ренты за год
Определение срока и размера ставки для постоянных непрерывных рент. Начнем с определения срока для случая, когда исходной является современная стоимость данного потока платежей. Решим (4.48) относительно п,принимая во внимание, что
Аналогично для случая, когда исходной является наращенная сумма ренты, получим:
Пример 4.24. За какой срок наращенная сумма ренты вырастет в пять раз по сравнению с годовой суммой взносов, если последние осуществляются непрерывно и равномерно в пределах года? На взносы начисляются проценты, сила роста 8%. Здесь S/R = 5,
Что касается определения силы роста по всем остальным заданным параметрам ренты, то здесь возникают те же затруднения, с которыми мы встретились при решении аналогичной задачи для дискретной ренты. Наиболее простым выходом является интерполяция и метод Ньютона — Рафсона (см. параграф 4.4). Остановимся на последнем. Исходная функция:
Разделим это выражение на R и умножим на
после чего находим производную:
На основе формулы (4.41) получим искомое выражение:
Пример 4.25. Какова доходность инвестиций, измеренная в виде силы роста, если затрачено 1000 млн. руб.? Годовая отдача ожидается в размере 200 млн. руб., поступающих равномерно в пределах года, срок отдачи — восемь лет. Воспользуемся интерполяционной формулой (4.40). Необходимо найти такое значение силы роста, которое удовлетворяло бы требованию A/R = 5 для n = 8. Зададимся двумя значениями ставки: 0,14 и 0,12. Им соответствуют
Находим первое приближение:
Проверка: при полученном значении силы роста
Применим теперь формулу (4.55). Пусть начальное значение
Проверка:
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 . Найдем коэффициент приведения такой ренты, обозначим его как
. Найдем коэффициент приведения такой ренты, обозначим его как  . Для этого необходимо найти предел коэффициента приведения p -срочной ренты при
. Для этого необходимо найти предел коэффициента приведения p -срочной ренты при  .
.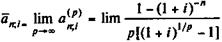
 в знаменатель приводит к неопределенности:
в знаменатель приводит к неопределенности: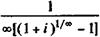
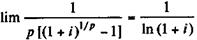
 (4.46)
(4.46) (4.47)
(4.47)
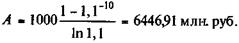
 , где
, где  — сила роста. Перепишем формулы (4.46) и (4.47), использовав эти соотношения. Получим:
— сила роста. Перепишем формулы (4.46) и (4.47), использовав эти соотношения. Получим: (4.48) (4.49)
(4.48) (4.49)
 = ln 1,1 = 0,09531, или 9,531%. Откуда
= ln 1,1 = 0,09531, или 9,531%. Откуда
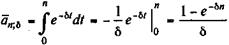
 . Его предел при
. Его предел при  составит:
составит:




 :
: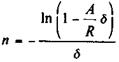 (4.50)
(4.50) (4.51)
(4.51)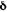 = 0,08, откуда согласно формуле (4.51)
= 0,08, откуда согласно формуле (4.51)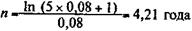
 (4.52)
(4.52)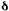 :
: (4.53)
(4.53)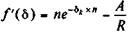 . (4.54)
. (4.54) . (4.55)
. (4.55)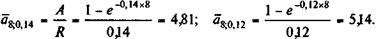

 = = A/R = 4,95 такая степень точности явно недостаточна, поэтому продолжим расчет, сокращая диапазон заданных значений силы роста. Пусть ставки, между которыми производится интерполяция, равны 0,125 и 0,13, тогда:
= = A/R = 4,95 такая степень точности явно недостаточна, поэтому продолжим расчет, сокращая диапазон заданных значений силы роста. Пусть ставки, между которыми производится интерполяция, равны 0,125 и 0,13, тогда:
 проверка A/R = 5,02. Как видим, уточнение ответа можно продолжить.
проверка A/R = 5,02. Как видим, уточнение ответа можно продолжить. = 0,12, тогда
= 0,12, тогда
 = 4,992.
= 4,992.


