
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ренты с постоянным абсолютным приростом платежейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В практике встречаются случаи, когда члены потоков платежей изменяются во времени. Такие изменения могут быть связаны с какими-либо обстоятельствами объективного порядка (например, условиями производства и сбыта продукции), а иногда и случайными факторами. Частным случаем такого потока является переменная рента. У последней члены потока изменяются по каким-то установленным (принятым, оговоренным и т.д.) законам или условиям развития. Если таких законов нет, то соответствующий поток можно назвать нерегулярным. Переменные потоки платежей встречаются относительно редко, во всяком случае существенно реже, чем постоянные. Ниже рассматриваются несколько видов переменных рент, причем с меньшей детальностью, чем были обсуждены постоянные ренты. Основное внимание уделено принципиальным зависимостям, знание которых позволяет разработать расчетные формулы для любых конкретных видов рент. Что касается нерегулярного потока платежей, то он здесь не анализируется, поскольку это было осуществлено в гл. 4 — см. формулы (4.1) и (4.2). Рента с постоянным абсолютным изменением членов во времени предполагает, что эти изменения происходят согласно арифметической прогрессии. Например, если выплачивается годовая рента постнумерандо, то размеры членов ренты образуют последовательность: R, R + a, R + 2 a,..., R + (n - 1) а. Величина t -гo члена такой ренты равна R + (t - l) a. Определим наращенную сумму и современную стоимость ренты. Для этого вернемся к общей формуле современной стоимости потока, заменив в ней Rt на члены рассматриваемого ряда. Получим: A = Rv + (R + a) v 2 +... + [ R + (t - 1) a ] vn, t = l... n. (5.1) Умножим это равенство на (1 + i) и вычтем из обеих сторон полученного выражения соответствующие стороны равенства (5.1): iA = R + av + av 2 +... + avn -1 - avn - (t - l) avn. После несложных преобразований находим:
Напомним, что an;i — современная стоимость постоянной ренты постнумерандо с членом, равным 1. Нетрудно видеть,что полученный результат представляет собой современную стоимость постоянной ренты с членом (R + a/i) за вычетом поправочной величины navn/i. Наращенную сумму такой ренты легко получить, умножив (5.2) на (1 + i) n. После чего
Определим теперь влияние на современную стоимость ренты абсолютного прироста платежей. Из формулы (5.1) следует, что A линейно зависит от a (см. рис. 5.1). (A 0 — современная стоимость потока платежей при нулевом их приросте.)
Полученная формула выгодно отличается от формулы (5.2) тем, что в ней показана роль каждого элемента взносов. Так, вклад "базового" платежа равен с,в свою очередь прирост платежей увеличивает современную стоимость ренты на ba. Аналогичным образом на основе формулы (5.3) получим линейную зависимость для S:
Как видим, коэффициенты b и b' в формулах (5.4) и (5.5) существенно зависят от уровня процентной ставки. Например, при i = 10% и n = 10 годам имеем b = 22,891, а для ставки, равной 20%, и том же сроке находим b = 12,887. Формулы (5.2) и (5.3) и их преобразования (5.4) и (5.5) получены для рент постнумерандо. Для рент пренумерандо находим:
Напомним, что Пример 5.1. Платежи постнумерандо образуют регулярный во временипоток, первый член которого равен 15 млн. руб. Последующие платежи увеличиваются каждый раз на 2 млн. руб. Начисление процентов производится по ставке 20% годовых. Срок выплат — десять лет. По условиям задачи: R = 15, а = 2, i = 20%, n = 10. Табличные значения коэффициентов a 10;2 = 4,192472, v 10 = 0,161505. Таким образом, по формуле (5.2) получим:
Используя взаимозависимость A и S, находим: S = 88,661 х 1,210 = 548,965 млн. руб. Или, применяя формулы (5.4) и (5.5):
Влияние изменений платежей здесь очевидно. Например, постоянная рента с R = 15 дает накопление в сумме около 390 млн. руб. Причем "вклад" прироста платежей в наращенную сумму составит почти 160 млн. руб., или примерно 20%. Продолжим пример. Пусть теперь рента предполагает систематическое сокращение платежей на 1 млн. в Год. Тогда по формулам (5.4) и (5.5) находим:
В частном случае, когда прирост равен величине первого члена потока платежей, т.е. R = а, получим на основе формул (5.2) и (5.3):
Иногда при анализе переменных рент может возникнуть "обратная" задача: определение первого члена ренты R или ее прироста а по всем остальным заданным параметрам ренты. Например, когда известна сумма, которую нужно аккумулировать за n лет, и необходимо разработать конкретный график взносов. Решив (5.2) или (5.3) относительно R, находим (для годовых рент постнумерандо):
В свою очередь, если определяется размер прироста при заданном R, то:
p -срочная переменная рента с постоянным абсолютным приростом. В этом случае последовательные выплаты равны:
Отдельный член этого ряда определяется как
где t — порядковый номер члена ренты. Для ренты постнумерандо находим при начислении процентов раз в году:
Пример 5.2. Ожидается, что сбыт продукции будет увеличиваться в течение двух лет — каждый квартал на 25 млн. руб. Первоначальный объем сбыта — 500 млн. руб. Определим наращенную сумму к концу срока при условии, что поступления денег — постнумерандо. По условиям задачи R = 500, a/p = 25, i = 20%, n = 2, рп = 8. Наращенная сумма к концу двухлетнего периода составит:
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.008 с.) |

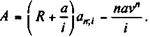 (5.2)
(5.2)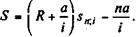 (5.3)
(5.3) (5.4)
(5.4)
 (5.5)
(5.5) (5.6)
(5.6)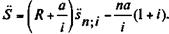 (5.7)
(5.7) — коэффициенты приведения и наращения дискретной постоянной ренты пренумерандо (см. параграф 4.5).
— коэффициенты приведения и наращения дискретной постоянной ренты пренумерандо (см. параграф 4.5).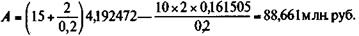
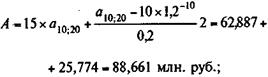

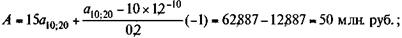



 (5.8)
(5.8)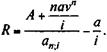 (5.9)
(5.9)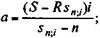 (5.10)
(5.10) (5.11)
(5.11)
 t = 1,2,..., pn,
t = 1,2,..., pn,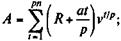 (5.12)
(5.12) (5.13)
(5.13)



