
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наращенная сумма постоянной ренты постнумерандоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Методом прямого счета, как это было показано в параграфе 4.2, можно найти наращенную сумму и современную стоимость любого потока платежей, в том числе и постоянной ренты. Однако удобнее, особенно в аналитических целях, воспользоваться более компактными формулами. Поскольку обобщающие характеристики постоянных рент играют существенную роль в анализе финансовых операций, получим эти формулы для всех видов постоянных рент, хотя для понимания существа дела достаточно разобраться с расчетом соответствующих характеристик годовой ренты. Годовая рента. Начнем с наиболее простого случая — годовой ренты постнумерандо. Пусть в течение п лет в банк в конце каждого года вносится по R руб. На взносы начисляются сложные проценты по ставке i % годовых. Таким образом, имеется рента, член которой равен R,асрок n. Все члены ренты, кроме последнего, приносят проценты — на первый член проценты начисляются n — 1 год, на второй п — 2 и т. д. На последний взнос проценты не начисляются (напомним, что рента постнумерандо). Наращенные к концу срока каждого взноса суммы составят: R (1 + i) n -1, R (1 + i) n -2,..., R (1 + i), R. Перепишем этот ряд в обратном порядке. Нетрудно убедиться в том, что он представляет собой геометрическую прогрессию со знаменателем (1 + i) и первым членом R. Число членов прогрессии равно п. Искомая величина очевидно равна сумме членов этой прогрессии. Отсюда
Обозначим множитель, на который умножается R,через sn;j; индекс n; j указывает на продолжительность ренты и величину процентной ставки. В дальнейшем этот множитель будем называть коэффициентом наращения ренты. Этот коэффициент представляет собой наращенную сумму ренты, член которой равен 1.
Таким образом, S = Rsn ; j. (4.6) Как видим, коэффициент наращения ренты зависит только от срока (числа членов ренты) и процентной ставки. С увеличением каждого из этих параметров его величина увеличивается. При i = 0 S = Rn, при n = 1 S = R. Значения коэффициента легко табулировать. Фрагмент такой таблицы приведен в Приложении, табл. 4. Пример 4.2. Для обеспечения некоторых будущих расходов создается фонд. Средства в фонд поступают в виде постоянной годовой ренты постнумерандо в течение пяти лет. Размер разового платежа 4 млн. руб. На поступившие взносы начисляются проценты по ставке 18,5% годовых. Поскольку в таблице коэффициентов наращения (Приложение, табл. 4) нет такого значения ставки, то необходимую величину определим по формуле (4.4). Величина фонда на конец срока составит:
S = 4 х s 5;18,3 = Заметим, что полученные выше формулы (4.4) и (4.5) могут применяться и для определения наращенной суммы p -срочной ренты. В этом случае переменная п означает число периодов, в свою очередь i является ставкой за период. Например, пусть рента постнумерандо выплачивается по полугодиям. Тогда в формуле (4.4) под n следует понимать число полугодий, а под i — сложную ставку за полугодие. Годовая рента, начисление процентов т раз в году. Пусть, как и выше, анализируется годовая рента постнумерандо. Однако проценты начисляются т раз в году. Члены ренты с начисленными к концу срока процентами образуют ряд (перепишем его в обратном порядке): R, R (1 + j/m) m, R (1 + j/m)2 m ,..., R (l + j/m)(n- 1) m , где j — номинальная ставка процентов. Нетрудно убедиться, что и в этом случае мы имеем дело с возрастающей геометрической прогрессией. Первый член прогрессии равен R,знаменатель — (1 + j/m) m. Сумма членов этой прогрессии равна
Пример 4.3. Несколько изменим условия примера 4.2. Пусть теперь проценты начисляются поквартально, а не раз в году. Имеем j/m = 18,5/4, тп = 20.
Как видим, переход от годового начисления процентов к поквартальному несколько увеличил наращенную сумму. Рента p -срочная (т = 1). Пусть рента выплачивается р раз в году равными суммами, процент начисляется один раз в конце года. Если годовая сумма платежей равна R,то каждый раз выплачивается R/p. Общее число членов ренты равно пр. Ряд членов ренты с начисленными процентами представляет собой геометрическую прогрессию. Первый член ее равен R/p,знаменатель — (1 + i) 1 / p. Сумма членов этой прогрессии:
Пример 4.4. Опять вернемся к условиям примера 4.2. Допустим, теперь платежи выплачиваются поквартально: R/p - 1 млн. руб., общее число платежей равно 20. Наращенная сумма составит S = 4 Рента p -срочная (р = m). На практике часто встречаются случаи, когда число выплат в году равно числу начислений процентов, т. е. когда р = т. Для получения необходимой формулы воспользуемся формулой (4.4), в которой i заменяется на j/m,а вместо числа лет берется число периодов выплат ренты пр,член ренты равен R/p. Поскольку р = т, то в итоге получим:
Искомая величина может быть получена и по формуле (4.4). В этом случае вместо числа лет подставляем в формулу число периодов, а вместо годового члена ренты — выплату за период, кроме того, вместо годовой ставки берется ставка за период. Пример 4.5. Продолжим наш сквозной пример 4.2 - 4.4. Пусть выплата членов ренты и начисление процентов производятся поквартально. По формуле (4.9) получим: S = 4 или по формуле (4.4):
Рента p -срочная (p<>m). Определим теперь наращенную сумму для наиболее общего случая — p -срочная рента с начислением процентов т раз в году. Общее количество членов ренты равно пр, величина члена ренты R/p. Члены ренты с начисленными процентами образуют ряд, следующий геометрической прогрессии, с первым членом R/p и знаменателем (1 + j/m)m/p. Сумма членов такой прогрессии составит:
Пример 4.6. Если в ренте, наращенная сумма которой определялась в предыдущем примере, начисление процентов производится ежемесячно, то
Непрерывное начисление процентов. Обсуждение методов определения наращенных сумм дискретных рент будет неполным, если не охватить ренты с непрерывным начислением процентов. Перепишем в обратном порядке ряд платежей с начисленными непрерывными процентами. Пусть это будут ежегодные платежи постнумерандо. Получим
где е — основание натуральных логарифмов, Аналогично для p -срочной ренты находим:
Пример 4.7. Если бы в условиях примера 4.2 вместо ежегодного начисления процентов предусматривалось непрерывное их начисление, причем сила роста была бы равна 18,5%, то: S = 4 При ежеквартальной выплате членов ренты получим: S = 4 Заметим, что непрерывное начисление процентов членов дискретной ренты дает в итоге такую же сумму, что и наращение по дискретной ставке i или j, если сила роста эквивалентна этим ставкам. Продемонстрируем сказанное. Сила роста, эквивалентная годовой ставке 18,5% согласно формуле (3.31), составит S = 4 Сравнение результатов наращения годовых и p -срочных рент постнумерандо с разными условиями выплат и наращения процентов. Как видно из приведенных примеров, условия выплат (точнее, их частота) и наращения процентов заметно влияют на размер наращенной суммы. Для практика, очевидно, представляет определенный интерес соотношение этих сумм. Ниже сравниваемые суммы обозначены как S (p; m):так, S (1;1) означает наращенную сумму годовой ренты с ежегодным начислением процентов, S (1; m) — аналогичную характеристику для ренты с начислением процентов т раз в году, наконец, S(p; Для одних и тех же сумм годовых выплат, продолжительности рент и размеров процентных ставок (i = j =
Приведенные неравенства могут быть использованы при выборе условий контрактов, так как позволяют заранее (до расчета) получить представление о приоритете того или иного условия. Например, можно заранее сказать, что рента с условиями р = 2 и т = 4 дает меньшую наращенную сумму, чем с р = 4 и т = 2 при равенстве всех прочих условий.
Для иллюстрации приведем значения S (p; m)для ренты с параметрами п = 10, R = 10, i =j =
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 801; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.250.235 (0.012 с.) |

 (4.4)
(4.4) (4.5)
(4.5) = 28,9 млн. руб.
= 28,9 млн. руб.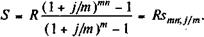 (4.7)
(4.7)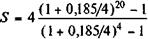 = 29,663 млн руб.
= 29,663 млн руб.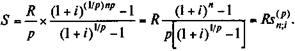 (4.8)
(4.8) = 30,834 млн. руб.
= 30,834 млн. руб. (4.9)
(4.9) = 31,785 млн. руб.
= 31,785 млн. руб. = 31,785 млн. руб.
= 31,785 млн. руб. (4.10)
(4.10)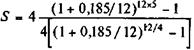 = 32, 025 млн руб.
= 32, 025 млн руб. . Сумма членов этой прогрессии равна
. Сумма членов этой прогрессии равна (4.11)
(4.11) — сила роста.
— сила роста. (4.12)
(4.12) = 29,955 млн. руб.
= 29,955 млн. руб. = 32,150 млн. руб.
= 32,150 млн. руб.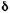 = ln (1 + + 0,185) = 0,16974. Тогда для годовой ренты находим:
= ln (1 + + 0,185) = 0,16974. Тогда для годовой ренты находим: = 28,900 млн руб. (см. пример 4.2).
= 28,900 млн руб. (см. пример 4.2). ) — наращенную сумму р -срочной ренты с непрерывным начислением процентов.
) — наращенную сумму р -срочной ренты с непрерывным начислением процентов. ) получим следующие соотношения:
) получим следующие соотношения: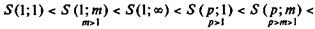
 (4.13)
(4.13) = 6%:
= 6%:



