
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По определению наращенной суммы рентыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Замечание: Воспользовались формулой возрастающей геометрической прогрессии:
Тогда общая формула наращенной суммы ренты будет иметь вид:
Пример 1. Создается фонд. Средства в фонд поступают в виде годовой постоянной ренты в течении 6 лет в конце года. Размер разового годового платежа 20 тыс. руб. На поступившие взносы начисляются 25% годовых. Найти величину фонда к концу срока.
Решение: Рассматривается годовая рента постнумерандо, член ренты R=20 тыс. руб., срок ренты n=6 лет, ставка i=25%. Величина фонда к концу срока 2. Годовая рента, постнумерандо, начисление процентов m раз в году, выплаты p один раз в году (Характеристики ренты R, n, j, m¹1, p=1) Наращенная сумма ренты Пример 2. В условиях примера 1 найти величину фонда к концу срока, если проценты начисляются ежеквартально, т.е. m=4. Решение:
Внимание! Наращенная стоимость возрасла. Следовательно, чем чаще начисляются проценты, тем больше S. 3. Рента p-срочная постнумерандо, проценты начисляются один раз в году, выплаты p раз в году (Характеристики ренты R, n, i, m=1, p¹1) Наращенная сумма ренты Пример 3. В условиях примера 1 найти величину фонда к концу срока, если выплаты делаются ежеквартально, т.е. p=4. Решение:
4. Рента p-срочная постнумерандо, проценты начисляются m раз в году, число выплат в году p равно числу начислений процентов m (Характеристики ренты R, n, j, m=p¹1) Наращенная сумма ренты Пример 4. В условиях примера 1 найти величину фонда к концу срока, если проценты начисляются ежеквартально, т.е. m=4, число выплат в году также равно p=4. Решение:
5. Рента р – срочная, проценты начисляются m раз в году, выплаты p не совпадают с начислением процентов (Характеристики ренты R, n, j, Наращенная сумма ренты Пример 5. В условиях примера 1 найти величину фонда к концу срока, если выплаты делаются ежемесячно, т.е. m=12, число выплат в году равно p=4. Решение:
6. Рента годовая постнумерандо, проценты начисляются непрерывно (Характеристики ренты R, n, d, p=1). Наращенная сумма ренты Пример 6. В условиях примера 1 найти величину фонда к концу срока, если непрерывная ставка d = 25%. Решение: 7. Годовая рента пренумерандо, проценты начисляются один раз в году (Характеристики ренты R, i, n, m=1, p=1)
Положим, что n =4 года и выведем формулу наращенной суммы ренты. Снова применим сумму геометрической прогрессии (см. выше ренту постнумерандо)
Наращенная сумма ренты
Наращенная сумма ренты пренумерандо больше наращенной суммы постнумерандо с такими же параметрами в (1+i) раз!
Пример 7. В условиях примера 1 найти величину фонда к концу срока, если выплаты делаются ежегодно в начале года. Решение: Рента годовая пренумерандо.
Современная стоимость ренты Под современной стоимостью А потока платежей понимают сумму всех его членов, дисконтированных на начало срока ренты. 1. Годовая рента постнумерандо (Характеристики ренты R. n, i, p=1, m=1). Схема дисконтирования:
Пусть n=4 года. Найдем современную стоимость ренты.
Замечание: Воспользовались формулой суммы убывающей геометрической прогрессии
Современная стоимость ренты сроком n лет
Пример 8. Рента постнумерандо характеризуется следующими параметрами: Член ренты R=4 млн. руб., срок ренты n=5 лет, годовая ставка i = 18,5%. Найти сегодняшнюю стоимость ренты.
Полученная сумма означает, что если сегодня положить 12,368 млн. руб. под годовую ставку18,5%, то в течении 5 лет в конце каждого года можно получать по 4млн. руб. 2. Годовая рента постнумерандо, начисление процентов m раз в году (Характеристики ренты R, n, j, m¹1, p=1) Современная стоимость
3. Рента р-срочная постнумерандо, проценты начисляются 1 раз в году (Характеристики ренты R, n, i, m=1, p¹1) Современная стоимость
4. Рента р-срочная постнумерандо, проценты начисляются m раз в году, число выплат p совпадает с числом начисления процентов m (Характеристики ренты R, n, j, m=p¹1) Современная стоимость
5. Рента р-срочная постнумерандо, проценты начисляются m раз в году, периоды выплат p не совпадают с периодами начислений процентов (Характеристики ренты R, n, j, m¹p¹1) Современная стоимость
6. Вечная рента постнумерандо В последней формуле современной стоимости ренты увеличим срок ренты n до бесконечности (n®¥). Коэффициент приведения ренты аni стремится к величине
7. Годовая рента пренумерандо (Характеристики ренты R, n, i, m=1, р=1) Схема дисконтирования
Современная стоимость ренты
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 955; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |




 - коэффициент наращения ренты, будем находить его, пользуясь математическим калькулятором.
- коэффициент наращения ренты, будем находить его, пользуясь математическим калькулятором.




 .
.
 )
) .
.
 .
.


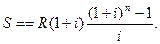





 - коэффициент приведения ренты.
- коэффициент приведения ренты.
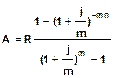 ;
; ;
; ;
; .
. , поэтому современная величина такой ренты, называемой вечной, имеет вид
, поэтому современная величина такой ренты, называемой вечной, имеет вид
 .
.
 .
.


