Определение срока платежа и процентных ставок

При разработке условий финансовых операций часто сталкиваются с необходимостью решения обратных задач — расчета продолжительности ссуды или уровня процентной ставки. Для простых процентов эти задачи рассмотрены в гл. 1. Обратимся к операциям со сложными процентными ставками и решим уравнения, связывающие Р и S, относительно интересующих нас величин. Ниже приводятся полученные результаты.

Срок платежа. Приведем формулы расчета п для различных условий наращения процентов и дисконтирования. При наращении по сложной годовой ставке i и по номинальной ставке j соответственно получим:

. (2.23) (2.24)

При дисконтировании по сложной годовой учетной ставке d и по номинальной учетной ставке f

. (2.25) (2.26)

При наращении по постоянной силе роста δ и по изменяющейся с постоянным темпом силе роста

. (2.27) (2.28)

Пример 2.15. За какой срок в годах сумма, равная 75 млн. руб., достигнет 200 млн. при начислении процентов по сложной ставке 15% раз в году и поквартально? По формулам (2.23) и (2.24) получим:

года (7 лет и 6 дней),

года (6 лет и 241 день).

Величина процентной ставки. Приведем формулы для расчета ставок i, j, d, f, δ для различных условий наращения процентов и дисконтирования. Они получены при решении уравнений, определяющих S и Р, относительно искомых ставок.

При наращении по сложной годовой ставке процентов и по номинальной ставке процента т раз в году находим

. (2.29) (2.30)

При дисконтировании по сложной учетной ставке и по номинальной учетной ставке

. (2.31) (2.32)

При наращении по постоянной силе роста

. (2.33)

При наращении по изменяющейся с постоянным темпом силе роста

. (2.34)

Пример 2.16. Сберегательный сертификат куплен за 100 тыс. руб., выкупная его сумма — 300 тыс. руб., срок — 2,5 года. Каков уровень доходности инвестиций в виде годовой ставки сложных процентов? По формуле (2.29) находим

, или 16,334%

Пример 2.17. Срок до погашения векселя равен двум годам. Дисконт при его учете составил 30%. Какой сложной годовой учетной ставке соответствует этот дисконт?

Применим формулу (2.31). По данным задачи Р/S = 0,7, откуда

, или 16,334%.

Кривые доходности

Любая ссудная или кредитная операция предполагает использование некоторого значения процентной ставки, с которым согласились обе стороны, участвующие в операции. Как уже говорилось выше, значение ставки зависит от многих факторов. Для практика важно представить себе закономерность изменения размера ставок, используемых в однородных по содержанию операциях, в зависимости от какого-либо фундаментального фактора. Вероятно, наиболее важным из таких факторов является риск невозврата ссуды. Очевидно, что подобного рода риск зависит от ряда факторов, среди которых очень важным является срок операции. Так, при всех прочих равных условиях ссуда на пять лет более рискованна, чем, скажем, на два года. Компенсировать риск владельцу денег может повышение доходности. Таким образом, зависимость "доходность — риск" приближенно можно охарактеризовать с помощью зависимости "доходность — срок", получить которую для практических целей существенно проще. Такую зависимость, представленную в виде графика, называют кривой доходности (yield curve). На графике по вертикали откладывают доходность (Y), по горизонтали — срок (п), см. рис. 2.6. Если график охватывает широкий диапазон сроков (как краткосрочные, так и долгосрочные операции), то для измерения срока применяют логарифмическую шкалу.

Наблюдаемые значения доходности обычно находятся около кривой или непосредственно на ней.

Итак, кривая доходности характеризует изменение доходности однородных кредитно-ссудных операций или финансовых инструментов (например, долгосрочных облигаций, акций компаний и т.д.) в зависимости от их срока. Конкретная кривая доходности отвечает реальной ситуации, сложившейся на денежно-кредитном рынке, и характерна для короткого временного периода. Изменение ситуации меняет форму кривой и ее положение на графике.

Для нормальных экономических условий кривая доходности имеет форму кривой А на рис. 2.6. Доходность растет по мере увеличения срока инвестиций. Причем каждая следующая единица прироста срока дает все меньшее увеличение доходности. Такую кривую называют положительной, или нормальной, кривой доходности (pozitive, normal yield curve). Нормальная форма кривой (не следует путать с кривой нормального распределения, используемой в статистике) наблюдается в условиях, когда инвесторы в своей массе учитывают такие факторы, как сокращение степени ликвидности и рост неопределенности финансовых результатов при увеличении срока.

Кривая доходности, близкая к горизонтальной прямой (кривая Б на рис. 2.6), указывает на то, что инвесторы не принимают во внимание или в малой степени учитывают риск, связанный со сроком.

Иногда встречаются "отрицательные" и "сгорбленные" кривые доходности. Первая соответствует уменьшению доходности по мере увеличения срока (нестабильность финансового рынка), вторая — падению доходности после периода некоторого ее роста.

Существуют две конкурирующие (а иногда дополняющие) теории, объясняющие "поведение" доходности — теория ликвидности и теория ожиданий. Первая изменение доходности связывает с увеличением риска ликвидности по мере увеличения срока. Именно с этой позиции объясняются выше положительная и горизонтальная кривые доходности. Согласно второй теории утверждается, что форма кривой может рассматриваться и как обобщенная характеристика ожиданий инвесторов, вернее, их поведения в текущий момент в связи с ожиданиями изменений процентных ставок в будущем. Однако интерпретация формы кривой в этом плане неоднозначна, да и не может быть иной, поскольку приходится принимать во внимание по крайней мере действие двух факторов — риска и ожидания изменений ставок. Например, положительная кривая иногда может интерпретироваться как указание на то, что инвесторы ожидают рост ставок в будущем. Однако чаще эта же форма кривой считается симптомом относительной стабильности денежно-кредитного рынка.

Кривые доходности получили широкое распространение как инструмент, помогающий при решении ряда инвестиционных проблем. В частности, при сравнении доходности разных финансовых инструментов (совмещение на одном графике нескольких кривых доходности), корректировке портфеля активов и т. д.

Пример 2.18. Рассмотрим на примере один из простых способов применения кривой доходности. Допустим, необходимо инвестировать некоторую сумму денег на четыре года. Причем в силу ряда причин у инвестора есть только два варианта для этого: разместить эту сумму на депозитах сразу на весь срок или сперва на три года, а затем на один год. Пусть уровни ставок следуют нормальной кривой доходности: по трехлетним депозитам — 10%, по четырехлетним — 10,5% сложных годовых. Размер ставки для депозита на один год (т.е. на четвертый год) в момент принятия решения, разумеется, неизвестен. Какой вариант размещения средств должен выбрать инвестор?

Очевидно, что при выборе второго варианта он должен иметь результат не хуже, чем при первом варианте. Задача, следовательно, сводится к определению того значения ставки для четвертого года, при котором оба варианта будут равноценными (эквивалентными) в финансовом отношении. Назовем такую ставку критической, или барьерной (break-even point).

Обозначим как i ₃ и i ₄ уровни процентных ставок для депозитов на три и четыре года, а через i ₀ — неизвестную критическую ставку для годового депозита. В силу финансовой эквивалентности результатов помещения средств множители наращения для обоих вариантов должны быть равными друг другу. Отсюда

(1 + i ₃)³(1 + i ₀) = (1 + i ₄)⁴

и, следовательно,

По данным примера находим критическую ставку i ₀ = 1,105⁴/1,1³ - 1 = 0,12014, или 12,014%.

Таким образом, для того чтобы инвестор остановился на втором варианте, он должен ожидать, что через три года ставка по одногодичным депозитам будет не менее 12,014 %, т.е. уровень ставок повысится. Соответственно, если он ожидает, что ставка не достигнет этого уровня, следует выбрать первый вариант.

Аналогичный расчет можно выполнить и для краткосрочной операции при использовании простых процентов. Продолжим пример и несколько изменим его условия. Пусть теперь срок измеряется не в годах, а в месяцах и приведены годовые ставки простых процентов. Остальные условия не изменены. В этом случае равенство множителей наращения записывается как

Отсюда

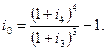
, или 11,707%.