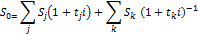Сложные проценты: определение срока ссуды, размера процентной ставки.

Т.к. и для простых процентов для сложных %-ов необходимо иметь ф-лы позволяющие определить недостающие параметра фин-ой операции: - срок ссуды n=logS/P/ log(1+i)= logS/P/log(1+j/n)^m; - ставка сложных %-ов i=ⁿ√S/P-1=(^{m n}√S/P -1)m.

 

14. Непрерывные проценты. Эквивалентность сложной и непрерывной ставок. Дисконтирующий множитель. Нахождение срока ссуды и силы роста. Все ситуации кот. мы до сих пор расм-им относим и дискретным %-ом поскольку их начисление осущ-ся зафик-ные промежутки времени. На практике не редко встречаются случаи, когда %-ты начис-ся непрерывно за сколько угодно малые промежутки времени. Если бы %-ты начис-сь бы ежедневно, то годовой коэф-т наращения выглядел бы так k_n=(1+j/m)^m=(1+j/365)³⁶⁵. Но по скольку %-ты начис-ся непрерывно, то m->∞: limk_y=lim[(1+j/m)^m/j]^j e^j; где e≈2,718281. Которые наз-ся числом Эйлера и яв-ся одной из важнейших постоянных матем-го анализа => можно записать фор-лу наращенной суммы для n-лет S=p*eⁱⁿ=p*e^{б n}. Ставку непрерывного %-та наз-ют силой роста и она обозначает (б)в отличии от ставки дискретных процессов (j).

 

15. Средние процентные ставки. Случай переменных ставок; случай переменных ставок и размеров ссуд. Как уже отмечалось, ставка в контракте может время от време: няться, т.е. быть плавающей. Для определения выгодности такого ко та, сравнения его с другими в смысле доходности можно найти сре процентную ставку, которая дает тот же результат наращения или д; тирования. Случай переменных ставок: а) простые ставки Средняя процентная ставка i находится по формуле: i_ср=∑n_t*i_t/N; где i, - простая ставка за период n_t, n₁ + п_г +... + n_k = N - общий срок сделки.Таким образом, i есть средняя арифметическая взвешенная с весами, равными продолжительности отдельных периодов.

Аналогично находится средняя дисконтная ставка:d_ср=∑n_t*d_t/N

б) сложные ставки Средняя процентная ставка i находится по формуле: i_ср=^N√(1+i₁)ⁿ¹*(1+i₂)ⁿ²*…*(1+i_k)^nk -1; где i_t-сложная ставка за период n₁+ п_г +...+ n_k = N - общий срок сделки. Как видно, в этом случае средняя ставка вычисляется как средняя взвешенная геометрическая. Случай переменных ставок и размеров ссуд. Если изменяются не только ставки, но и размеры ссуд, то в общем случае решение затруднительно. Несложное решение можно найти в частном случае, когда n₁, n₂,..., п_к одинаковы и равны п. Тогда имеем:

- для простых ставок i_ср=∑P_t*i_t/∑P_t.

- для сложных ставок: i_ср=ⁿ√∑P_t(1+i_t)ⁿ/∑P_t -1.

18. Эквивалентные ставки. Эквивалентность сложных дискретных и непрерывных ставок.

- замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяя финансовых отношений сторон в рамках одной операции.

Эквивалентность сложных дискретных и непрерывных ставок.

Теоретически можно найти соотношение эквивалентности между силой роста и любой дискретной процентной ставкой. Однако в этом нет необходимости. Ограничимся несколькими такими соотношениями, необходимость в которых может возникнуть в практических расчетах.

Эквивалентность б и i: б=ln(1+i); i=e ^б-1

Эквивалентность б u j: из равенства (1+j/m)^m=e ^б следует j=m(e ^б/m -1); б=m*ln(1+j/m)

Эквивалентность б и d: из равенства (1-d)^-1=e^б следует б=-ln(1-d); d=1- e^-б

Формулы эквивалентности дискретных и непрерывных ставок позволяют расширить применение непрерывных процентов. Как уже говорилось выше, непрерывные проценты во многих сложных расчетах позволяют существенно упростить выкладки. Вместе с тем такие ставки непривычны для практика, поэтому используя формулы эквивалентности, нетрудно представить полученные результаты в виде общепринятых характеристик.

 

19. Финансовая эквивалентность обязательств.

Эквивалентными считаются такие платежи, которые, будучи "приведенными" к одному моменту времени, оказываются равными. Приведение осуществляется путем дисконтирования (приведение к более ранней дате) или, наоборот, наращения суммы платежа (если эта дата относится к будущему). Если при изменении условий контракта принцип финансовой эквивалентности не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить.По существу, принцип эквивалентности в наиболее простом проявлении следует из формул наращения и дисконтирования, связывающих величины Р и S.

Сумма Р эквивалентна S при принятой процентной ставке и методе ее начисления. Две суммы денег S1 и S2, выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке и на один момент времени, одинаковы. Замена S1 на S2 в этих условиях формально не изменяет отношения сторон.

Сравнение платежей предполагает использование некоторой процентной ставки и, следовательно, его результат зависит от выбора ее размера. Однако, что практически весьма важно, такая зависимость не столь жестка, как это может показаться на первый взгляд. Допустим, сравниваются два платежа S1 и S2 со сроками n1 и n2, причем S1 < S2 и n1 < n2. Соотношение их современных стоимостей зависит от размера процентной ставки

С ростом i размеры современных стоимостей уменьшаются, причем при i = i0 наблюдается равенство Р1 = Р2 Для любой ставки i < i0 имеем Р1 < Р2. Таким образом, результат сравнения зависит от размера ставки, равного i0. Назовем эту ставку критической или барьерной. На основе равенства

S₁/(1+n₁i₀)= S₂/(1+n₂i₀)

находим барьерную ставку:

i₀=(1- S₁/ S₂)/((S₁/ S₂)n₂ – n₁)

Если дисконтирование производится по сложной ставке, то критическую ставку найдем из равенства

S₁(1+i₀)^-n1=S₂(1+i₀)^–n2

В итоге

i₀=(S₂/ S₁)^1/n2-n1-1

 

20. Барьерные ставки. Случай простых и сложных процентов Допустим, необходимо выбрать один из двух вариантов поступлений денежных средств, различающихся суммами и сроками: S₁, S₂ со сроками n₁, n₂, причем S₂ > S₁, n₂ > n₁ (иначе задача не имеет экономического смысла). Логически оправданно выбор обосновать на сравнении современных стоимостей поступлений. Таким образом, результат выбора зависит от ожидаемого рыночного уровня процентной ставки. Барьерной в рассматриваемой задачей является ставка, при которой оба варианта оказываются эквивалентными.

Рассмотрим метод решения для двух вариантов расчета современных стоимостей: по простой и сложной процентным ставкам. Для простой ставки имеем следующее равенство современных стоимостей (P₁ и P₂):

S₁/(1+n₁i_k)= S₂/(1+n₂i_k)

а для сложной ставки:

S₁(1+i_k)^-n1= S₂(1+i_k)^-n2

В обоих равенствах i_k означает величину барьерной ставки. Следовательно для простого %:

i_k= (S₂-S₁)/(S₁n₂- S₁n₁)

Из последнего выражения следует необходимое условие для существования барьерной ставки

S₁n₂> S₂n₁ или S₁ > S₂ (n₁/n₂)

Перейдем к определению барьерного значения сложной ставки.

(1+i_k)^n2-n1=S₂/S₁

откуда

ln(1+i_k)=(ln(S₂/S₁))/(n₂-n₁)

в итоге

i_k=antln(1+i_k)-1

21. Консолидирование (объединение) задолженности заключается в разработке так называемого уравнения эквивалентности, в котором сумма заменяемых платежей, приведенных к какому-либо моменту времени, приравнивается к сумме платежей по новому обязательству, приведенных к той же дате. Для краткосрочных обязательств приведение осуществляется обычно на основе простых ставок, для средне- и долгосрочных — с помощью сложных процентных ставок.

Одним из распространенных случаев изменения условий контрактов является консолидация платежей. Пусть платежи S₁, S₂,..., S_m со сроками n₁, n₂,…, n_m заменяются одним в сумме S₀ и сроком n₀. В этом случае возможны две постановки задачи: если задается срок n₀, то находится сумма S₀ и наоборот, если задана сумма консолидированного платежа S₀, то определяется срок n₀. Рассмотрим обе постановки задачи.

При применении простых процентных ставок получим:

 

где S_j — размеры объединяемых платежей со сроками n_j < n₀, S_k — размеры платежей со сроками n_k > n₀, t_j= n₀- n_j; t_k= n_k-n₀

На основе сложных процентных ставок:

Если при объединении платежей задана величина консолидированного платежа S0, то возникает проблема определения его срока n0. В этом случае уравнение эквивалентности удобно представить в виде равенства современных стоимостей соответствующих платежей.

При применении простой ставки это равенство имеет вид:

откуда:

Очевидно, что размер заменяющего платежа не может быть меньше суммы современных стоимостей заменяемых платежей. Заметим также, что искомый срок пропорционален величине консолидированного платежа.

Перейдем к определению срока консолидированного платежа на основе сложных процентных ставок. Уравнение эквивалентности запишем следующим образом:

У Для упрощения дальнейшей записи примем:

После чего находим:

 

иногда также применяют средний взвешенный срок:

22. Инфляция. Основные понятия. Критические ставки для случая простых и сложных процентов.

Инфляция – устойчивый рост среднего уровня цен на товары и услуги в эк-ке. Ее ходимо учитывать по крайней мере в двух случаях: при расчете наращенной суммы денег и при измерении реальной эффективности (доходности) финансовой операции. Введем обозначения:

S — наращенная сумма денег, измеренная по номиналу,

С — наращенная сумма с учетом ее обесценения,

J_p — индекс цен,

J_c — индекс, характеризующий изменение покупательной способности денег за период.

Очевидно, что

С= S * J_c.

Индекс покупательной способности денег, как известно, равен обратной величине индекса цен — чем выше цены, тем ниже покупательная способность:

J_c=1/ J_p

Указанные индексы, естественно, должны относиться к одинаковым интервалам времени. Нетрудно связать индекс цен и темп инфляции. Под темпом инфляции h понимается относительный прирост цен за период; обычно он измеряется в процентах и определяется как

h=100(J_p-1)

В свою очередь

J_p=(1+(h/100))

Пусть теперь речь пойдет о будущем. Если h — постоянный ожидаемый (или прогнозируемый) темп инфляции за один период, то за n таких периодов получим

J_p=(1+(h/100))ⁿ

Если наращение производится по простой ставке, то наращенная сумма с учетом покупательной способности равна

C=S/ J_p=P((1+ni)/ J_p)= P((1+ni)/(1+(h/100)ⁿ)

Как видим, увеличение наращенной суммы с учетом ее инфляционного обесценения имеет место только тогда, когда

1 + ni > Jp

Наращенная сумма по сложным процентам с учетом инфляционного обесценивания находится как

C=S/ J_p=P((1+i)ⁿ/ J_p)= P((1+i)/(1+(h/100)))ⁿ

 

 

23. Расчет брутто-ставки для случая простых и сложных процентов.

брутто-ставка – итоговая величина от компенсации потерь посредством корректировки ставки процента, по которой производится наращение, т.е. увеличение ставки на величину так называемой инфляционной премии

Определим брутто-ставку (обозначим ее как r) при условии полной компенсации инфляции. При наращении по сложной процентной ставке находим брутто-ставку из равенства

1+r=(1+i)(1+(h/100))

Откуда

r=i+(h/100)+i(h/100)

На практике скорректированную по темпу инфляции ставку часто рассчитывают проще, а именно:

r=i+(h/100)

При наращении по простым процентам имеем

r=((1+ni)J_p-1)/n

где J_p — индекс цен за учитываемый период.

Очевидно, что при больших темпах инфляции корректировка ставки имеет смысл только для кратко- или в крайнем случае среднесрочных операций.