
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды процентных ставок и способы начисления процентов. Простые проценты.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Виды процентных ставок и способы начисления процентов. Простые проценты. Основным свойством денег является их временная ценность, связанная с − наличием инфляции, − обращением капитала. Деньги, относящиеся к различным моментам времени, неравноценны, например, сегодняшние деньги ценнее будущих, а будущие, в свою очередь, менее ценны, чем сегодняшние при равенстве их сумм. Предмет финансовой математики – это специальные модели и алгоритмы, связанные с проблемой «деньги – время» и позволяющие оценить будущие доходы с позиции текущего момента. Основными задачами финансовой математики являются: − измерение конечных результатов финансовой операции; − разработка планов выполнения финансовых операций; − оценка зависимости конечных результатов операции от ее условий; − определение допустимых критических значений параметров операции и расчет параметров эквивалентного (безубыточного) изменения первоначальных условий финансовой операции. Любая финансовая операция, инвестиционный проект или коммерческое соглашение предполагают наличие ряда условий их выполнения, с которыми согласны участвующие стороны. К таким условиям относятся следующие количественные данные: − денежные суммы, − временные параметры, − процентные ставки. Под процентами, понимают абсолютную величину дохода от предоставления денег в долг в любой его форме: выдача ссуды, продажа товара в кредит, помещение денег на депозитный счет, учет векселя, покупка сберегательного сертификата или облигации и т.д. Под процентной ставкой понимается относительная величина дохода за фиксированный отрезок времени – отношение дохода (процентных денег) к сумме долга. Она измеряется в процентах. При выполнении расчетов процентные ставки обычно измеряются в десятичных дробях. Временной интервал, к которому приурочена процентная ставка, называют периодом начисления. В качестве такого периода принимают год, полугодие, квартал, месяц или даже день. Чаще всего на практике имеют дело с годовыми ставками. Проценты согласно договоренности между кредитором и заемщиком выплачиваются по мере их начисления или присоединяются к основной сумме долга (капитализация процентов). Процесс увеличения суммы денег во времени в связи с присоединением процентов называют наращениемэтой суммы. Возможно определение процентов и при движении во времени в обратном направлении – от будущего к настоящему. В этом случае сумма денег, относящаяся к будущему, уменьшается на величину соответствующего дисконта(скидки). Такой способ называют дисконтированием(сокращением). Размер процентной ставки зависит от: − общего состояния экономики, в том числе денежно-кредитного рынка; − кратковременных и долгосрочных ожиданий его динамики; вида сделки, ее валюты; срока кредита; − особенностей заемщика (его надежности) и кредитора, истории их предыдущих отношении и т. д. Простые проценты Под наращенной суммойссуды (депозита, инвестированных средств, платежного обязательства и т.п.) понимается ее первоначальная сумма с начисленными на нее процентами к концу срока наращения.Величина наращенной суммы представляет собой произведение первоначальной суммы ссуды на множитель наращения, который показывает во сколько раз наращенная сумма больше первоначальной.В зависимости от применяемой процентной ставки и условий наращения формула расчета множителя наращения записывается по-разному. Например, для наращения по простым процентам наращенная сумма (S) будет рассчитываться так:
где Р – первоначальная сумма ссуды, ден. ед.; п –срок ссуды (а днях, месяцах, годах и т. п.); i – ставка наращения (простая постоянная), ед. Выражение (1 + ni) называется множителем наращения. В финансово-экономических расчетах срок ссуды обычно измеряется годами, поэтому значение ставки наращения i есть значение годовой ставки процентов. Проценты, начисленные за весь срок ссуды, в этом случае составят:
где I – процентная сумма (величина дохода), ден. ед. Представленная выше формула называется формулой простых процентов, а величину I можно определить как процентный доход, или процентные деньги (проценты). В практической работе банки, коммерческие организации, финансовые институты и т.п. используют различные способы изменения числа дней ссуды (t) и продолжительности года ( временной базыдля расчета процентов) в днях (К).В зависимости от того, как определяются величины t и К– точно, или приблизительно применяются следующие варианты («практики», «системы») начисления простых процентов. 1. Точные проценты с фактическим числом дней ссуды(так называемая «английская» практика).Этот вариант дает самые точные результаты и применяется многими центральными и крупными коммерческими банками мира. В этом случае K=365 дням, а в месяцах 28, 29, 30 и 31 день. 2. Обыкновенные проценты с точным числом дней ссуды(так называемая «французская»практика или банковский метод).Этот вариант дает несколько больший результат, чем применение точных процентов.Так, если число дней ссуды превышает 360, то данный способ измерения времени приводит к тому, что сумма начисленных процентов будет больше, чем предусматривается годовой ставкой. Например, при t = 363 дням, n=363:З60=1,0083, а множитель наращения за этот период будет равен: 1+1,0083*i. 3.Обыкновенные проценты с приближенным числом днейссуды («германская»практика). Подсчет числа дней в этом варианте базируется на годе в 360 дней и месяцах по 30 дней. Поскольку точное число дней ссуды в большинстве случаев больше приближенного, то проценты с точным числом дней обычно больше, чем с приближенным, a следовательно, и наращенная сумма по процентам с точным числом дней обычно выше. Наращение суммы в случае изменения простой процентной ставки в течение срока ссуды.На практике часто встречается ситуация, когда кредитные договоры (соглашения) предусматривают изменение процентной ставки в течение срока ссуды (например, в связи с изменением ставки рефинансирования; желанием банка учесть темп инфляции и т. д.). При этом годовая ставка процентов, указанная в кредитном договоре, носит название номинальной.В этом случае наращенная сумма будет исчисляться следующим образом:
где it, – ставка простых процентов в периоде t; t=l,2,...,m; ед.; nt, – продолжительность периода; т – число периодов, ед. Наращение суммы при реинвестировании.В целях повышения заинтересованности вкладчиков и быстрого привлечения дополнительных денежных средств, например, в кратко- и среднесрочные депозиты, банки и финансовые компании могут предлагать производить своим клиентам неоднократное наращение вложенной суммы в пределах общего срока займа, т.е. реинвестировать ее. Иными словами, реинвестирование предполагает присоединение начисленных процентов к исходной (первоначальной) сумме и начисление процентов уже на возросшую сумму, и так несколько раз за период.При таком реинвестировании наращенная сумма рассчитывается по формуле:
где n1,n2,...nt – продолжительность периодов наращения, лет; причем i1, i2, … it, – ставки реинвестирования, ед. В частном случае, когда
где m – число операций реинвестирования, ед. Пример 1.1. На сумму вклада в размере 50 тыс. р. в течение месяца начисляются простые проценты по ставке 24% годовых. Какова будет наращенная сумма, если эта операция будет повторена в течение 6 мес. текущего года (т.е. при реинвестировании этой суммы шесть раз) при расчете точных процентов с фактическим числом дней ссуды с 1 -го марта? Решение. По условиям примера Р = 50 тыс. р.; i = 0,24. Точное число дней не високосного года, начиная с марта и заканчивая августом составит: 31+30+31+30+31->-31=184 дня. По формуле
Пример 1.2. Потенциальный клиент ряда надежных и расположенных в пределах его пешеходной доступности банков города имеет временно свободные денежные средства в размере 10 тыс. р. и хотел бы поместить их на депозитный счет сроком на 1 год. Первый банк (банк А) предлагает ему сделать вклад на условиях ежеквартального начисления по ставке 20% годовых и капитализации (реинвестирования) процентов. Второй банк (банк Б) на следующих условиях: начисление на вклад по ставке 24% годовых дважды в год с капитализацией процентов. Банк В предлагает ежемесячное начисление процентов по ставке 20% годовых и капитализацией начисленных процентов. И, наконец, банк Г предлагает сделать вклад на условиях начисления 25% годовых без капитализации процентов и начисления их в конце срока вклада. В каком из банков вкладчик может получить наибольшую сумму по окончании срока договора? Решение. По условиям примера Р = 10тыс. р.; i1 = 20%; i2 = 24%; i3 = 20%; i4 = 25%. Учитывая, что начисление процентов происходит ежеквартально, по полугодиям и ежемесячно с капитализацией, и только в банке Г – в конце года (без реинвестирования), по формуле
Наращенная сумма при вкладах в конце и в начале каждого года. Довольно часто по условиям договоров вклада депозитных договоров банки предусматривают возможность довложения определенной (часто – не выше первоначальной) денежной суммы. В случае если вклады делаются в конце каждого года, то наращенная сумма составит:
где m – число вкладов, ед.; D – величина вклада, ден. ед. Если вклады по своей величине равны, т.е. D1=D2=D3=Dm, То формулу можно записать так: или, учитывая, что можно окончательно написать: Очевидно, что наращение по ставке простых процентов в случае, когда довложения делаются в начале года, существенно выгоднее по сравнению в довложениями в конце года.Это происходит потому, что в первом случае увеличивается на один год наращения. Расчет суммы необходимого депозита при ежегодных выплатах. Довольно часто (особенно при работе с клиентами – пенсионерами, со вкладами на несовершеннолетних и т.п.) работники банка, работающие со вкладами населения, сталкиваются с задачей определения необходимой первоначальной суммы вклада (депозита) клиента, который смог бы обеспечить ему определенные ежегодные выплаты в течении n лет по заранее оговоренной ставке процентов. В общем случае эта задача сводится к решению задачи определения «вечной» ренты, которая подробно будет рассмотрена ниже. Сейчас же рассмотрим ее решение исходя из тех знаний, которые мы уже имеем. Используя формулу
где Р1,Р2,…,Рn – определенные ежегодные выплаты, ден, ед.; п – время выплат, лет. При условии равенства ежегодных выплат, т.е. при P1 =P2 = Р3 = Рn формулу можно преобразовать в выражение следующего вида:
Для приближенных, оценочных расчетов величины первоначального вклада можно использовать примерное равенство выражений:
Пример 1.3. Рассчитать необходимую первоначальную величину депозита клиента для того, чтобы он имел возможность ежегодно в течении 5 лет получать со своего счета в банке сумму в размере 6 тыс. руб. при начислении простой процентной ставки, равной 30% годовых. Решение По условиям примера Р=6 тыс. руб.; in=30%; n=5 лет. Используя формулу
Расчет по формуле
Расхождение по сравнению с результатом, полученным по первой формуле, равно – 0,046 тыс. руб., или менее 0,3%. Как видим, расчет по второй формуле дает вполне приемлемый результат. Расчет срока ссуды и уровня процентной ставки.При подготовке обоснования для получения ссуды и расчета ее эффективности возникает задача определения срока ссуды и уровня процентной ставки при имеющихся прочих условиях. В этом случае срок ссуды может быть определен как в годах, так и в днях: в годах в днях Соответственно и размер процентной ставки может быть определен при исчислений срока ссуды в годах как: а при исчислении срока ссуды в днях так: Наращение и равномерная выплата процентов в потребительском кредите. В потребительском кредите, т.е. кредите, как правило, на личные нужды для приобретения товаров (или услуг) проценты начисляются на всю сумму кредита и присоединяются к основному долгу чаще всего уже в момент открытия кредита. Такой подход называется разовым начислением процентов, апогашение долга с процентами в этом случае производится обычно равными суммами на протяжении всего срока кредита. Наращенная сумма долга при таком подходе рассчитывается по формуле
где т – число погасительных платежей по кредиту в году, ед. Заметим, что в связи с тем, что проценты начисляются на первоначальную сумму долга, а фактическая его величина постоянно уменьшается со временем, действительная процентная ставка (по фактически использованному кредиту) оказывается заметно выше, чем ставка по первоначальным договорным условиям. Вопросы для самопроверки: 1. Что является предметов финансовой математики? 2. Какую роль играет время в финансовых расчетах? 3. Перечислите виды процентных ставок. 4. Что такое наращенная сумма? 5. Что такое дисконтирование? 6. Как определяется величина процентной ставки? 7. Как рассчитывается срок ссуды.
Тема 3.1.-3.2. Понятие эквивалентности процентных ставок. Вывод формул эквивалентности процентных ставок на основе равенства множителей наращения. Принцип финансовой эквивалентности обязательств. Уравнение эквивалентности. Объединение (консолидация) платежей. Вопросы для рассмотрения: 1. Эквивалентность процентных ставок. Общие принципы. 2. Эквивалентность простой и сложной процентной ставки с начислением процентов 1 раз в год. 3. Эквивалентность простой процентной ставки и сложной с начислением процентов m раз в год. 4. Эквивалентность сложной процентной ставки с начислением процентов 1 раз в год и сложной процентной ставки с начислением процентов m раз в год. 5. Эквивалентность непрерывной процентной ставки и простой процентной ставки. 6. Эквивалентность непрерывной процентной ставки и сложной процентной ставки с начислением 1 раз в год. 7. Эквивалентность непрерывной процентной ставки и простой процентной ставки с начислением m раз в год. 8. Средняя процентная ставка. 9. Финансовая эквивалентность обязательств.
1. Принцип финансовой эквивалентности обязательств В финансовой практике часто возникают ситуации, когда необходимо заменить одно обязательство другим, например, с более отдаленным сроком платежа, досрочно погасить задолженность, объединить несколько платежей в один (консолидировать платежи), изменить схему начисления процентов и т. п. Таким общепринятым принципом, на котором базируются изменения условий контрактов, является финансовая эквивалентность обязательств. Изменение условий контракта основывается на принципе финансовой эквивалентности обязательств, который позволяет сохранить баланс интересов сторон контракта. Этот принцип предполагает неизменность финансовых отношений до и после изменения условий контракта. При изменении способов начисления процентов необходимо учитывать взаимозаменяемость между различными видами процентных ставок. Эквивалентными называются процентные ставки, которые при замене одной на другую приводят к одинаковым финансовым результатам, т.е. отношения сторон не изменяются в рамках одной финансовой операции. При изменении условий платежей также необходимо учитывать разновременность платежей, которые производятся в ходе выполнения условий контракта до и после его изменения. Эквивалентными считаются такие платежи, которые оказываются равными после их приведения по заданной процентной ставке к одному моменту времени, либо после приведения одного из них к моменту наступления другого по заданной процентной ставке. Приведение осуществляется путем дисконтирования (приведение к более ранней дате) или, наоборот, наращения суммы платежа (если эта дата относится к будущему). Если при изменении условий контракта принцип финансовой эквивалентности не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить.
2. Эквивалентность процентных ставок Для нахождения значений эквивалентных процентных ставок следует составлять уравнение эквивалентности. Эквивалентность простой процентной и простой учетной ставок. Исходные уравнения для вывода эквивалентности S = P (1 + n ∙ i) и Если результаты наращения равны, то получаем уравнение P (1 + n ∙ i) = Отсюда 1 + n ∙ i =
Для одних и тех же параметров ссуды условие эквивалентности приводит к тому, что d < i. При этом с ростом срока финансовой операции различие между ставками увеличивается. Пример 1. Определить простую учетную ставку, эквивалентную ставке обычных процентов 12 % годовых, при наращении за 2 года. Решение. Параметры задачи: n = 2 года, i = 12 %. Тогда d = 0,12/(1 + 2 ∙ 0,12) = 0,0968 или 9,7 %. Следовательно, операция, в которой принята учетная ставка 9,7 %, дает тот же финансовый результат для 2-годичного периода, что и простая ставка 12 % годовых.
Эквивалентность простой и сложной процентных ставок. Наращенные суммы по простой и сложной процентным ставкам равны
Если равны результаты наращения, то уравнение эквивалентности
Отсюда При начислении процентов m раз в году аналогично рассуждая, получим: Пример 2. Предполагается поместить капитал на 4 года либо под сложную процентную ставку 20 % годовых с полугодовым начислением процентов, либо под простую процентную ставку 26 % годовых. Найти оптимальный вариант. Решение. Параметры задачи: n = 4 года, m = 2, i с = 20 %, i п = 26 %. Находим для сложной процентной ставки эквивалентную простую ставку:
Таким образом, эквивалентная сложной ставке, по первому варианту, простая процентная ставка составляет 28,59 % годовых, что выше предлагаемой простой ставки в 26 % годовых по второму варианту. Следовательно, выгоднее разместить капитал по первому варианту, т.е. под 20 % годовых с полугодовым начислением процентов. Пример 3. По трёхмесячному депозиту назначена ставка 10,2 % годовых. Какую ставку годовых процентов следует назначить на ежемесячные депозиты, чтобы последовательное переоформление этих депозитов привело к такому же результату, что и использование трёхмесячного депозита, если пренебречь двумя днями, которые теряются при переоформлении депозитов (T =360)? Решение. Приравняем соответствующие множители наращения:
Отсюда получаем, что i = 0,101 1 или 10,11 %.
Простые проценты. Наращенная сумма при отсутствии инфляции равна Это ставка, скорректированная на инфляцию, называется брутто-ставкой. Сложные проценты. Проценты 1 раз в год: Наращенная сумма при отсутствии инфляции равна Проценты m раз в год: При начислении процентов несколько раз в год:
Эти модели позволяют производить учет инфляции и корректировку процентных ставок. Годовая ставка сложных процентов, обеспечивающая реальную доходность кредитной операции, определяется по формуле Фишера, связывает три показателя: R – номинальная процентная ставка, α – уровень инфляции r – реальная процентная ставка (доходность финансовой операции)
Пример 4.1. Годовой темп инфляции 20%. Банк рассчитывает получить 10% реального дохода в результате предоставления кредитных ресурсов. Какова номинальная ставка, по которой банк предоставит кредит?
На практике довольно часто довольствуются сравнением i и τ путем вычисления реальной ставки, т.е. уменьшенной ставки доходности на уровень инфляции: i = (i - τ) / (1 + τ) Поскольку покупательная способность денег снижается в условиях инфляции, то происходит обесценивание денежных доходов. Поэтому при наращении денег на депозите вкладчик должен сопоставить номинальную процентную ставку, т.е. ставку, указанную в договоре, с величиной индекса потребительских цен. Вычисление наращенных сумм Получаем формулу: Реальная стоимость С суммы S, обесцененная во времени за счет инфляции при индексе цен Если наращение производится по простой ставке в течение n лет, то Для определения реальной покупательской способности, наращенную сумму необходимо привести ее к ценам базового периода: Вследствие начисления процентов происходит увеличение денежных сумм, но их стоимость под влиянием инфляции уменьшается. Поскольку каждая денежная единица обесценивается вследствие инфляции, то в дальнейшем обесцениваются уже обесцененные деньги. Наращение осуществляется по простым или сложным процентам, но инфляция всегда оценивается по сложному проценту. Наращенная сумма за n лет с учетом ее обесценивания составит: − Если темп инфляции больше ставки начисляемых процентов, то полученная наращенная сумма не компенсирует потерю покупательной способности денег. Банковская ставка называется отрицательной. − Если темп инфляции меньше ставки начисляемых процентов, то наблюдается реальный рост покупательной способности денег. Банковская ставка называется положительной. − Если темп инфляции равен ставке начисляемых процентов, то покупательная способность наращенной суммы равна покупательной способности первоначальной суммы. Вопросы для самопроверки: 1. Что такое инфляция? Перечислите виды инфляции. 2. Что такое ИПЦ? 3. С какой целью проводят учет инфляции? 4. Что такое номинальная ставка процента? Чем она отличается от реальной ставки? 5. Что такое финансовая операция? 6. Как измерить реальную доходность финансовой операции? Тема 5.1.-5.2. Понятия видов потоков платежей и их основные параметры. Понятие финансовой ренты. Основные параметры ренты и их вычисление. Различные виды финансовых рент. Виды переменных рент. Постоянная непрерывная рента. Конверсии рент. Вопросы для рассмотрения: 1. Ренты. Классификация рент. 2. Наращенная сумма финансовой ренты постнумерандно. 3. Современная величина финансовой ренты постнумерандно. 4. Срок финансовой ренты постнумерандно. 5. Член финансовой ренты постнумерандно. 6. Наращенная сумма и современная величина других типов финансовых рент. 7. Определение параметров других типов финансовых рент. 8. Определение процентной ставки финансовой ренты.
Очень часто в контрактах финансового характера предусматриваются не отдельные разовые платежи, а серию платежей, распределенных во времени. Примерами могут быть регулярные выплаты с целью погашения долгосрочного кредита вместе с начисленными на него процентами, периодические взносы на расчетный счет, на котором формируется некоторый фонд различного назначения (инвестиционный, пенсионный, страховой, резервный, накопительный и т.д.), дивиденды, выплачиваемые по ценным бумагам, выплаты пенсий из пенсионного фонда и пр. Ряд последовательных выплат и поступлений называют потоком платежей. Выплаты представляются отрицательными величинами, а поступления - положительными. Обобщающими характеристиками потока платежей являются наращенная сумма и современная величина. Каждая из этих характеристик является числом. Наращенная сумма потока платежей - это сумма всех членов последовательности платежей с начисленными на них процентами к концу срока ренты. Под современной величиной потока платежей понимают сумму всех его членов, дисконтированных (приведенных) на некоторый момент времени, совпадающий с началом потока платежей или предшествующий ему. Конкретный смысл этих обобщающих характеристик определяется природой потока платежей, причиной, его порождающей. Например, наращенная сумма может представлять собой итоговый размер формируемого инвестиционного или какого-либо другого фонда, общую сумму задолженности. Современная величина может характеризовать приведенную прибыль, приведенные издержки. 5.1. Понятие финансовой ренты (аннуитета) Поток платежей, все члены которого положительные величины, а временные интервалы постоянны, называют финансовой рентой или аннуитетом. Финансовая рента имеет следующие параметры: член ренты - величина каждого отдельного платежа, период ренты - временной интервал между двумя соседними платежами, срок ренты - время, измеренное от начала финансовой ренты до конца ее последнего периода, процентная ставка - ставка, используемая при наращении или дисконтировании платежей, образующих ренту, число платежей в году, число начислений процентов в году, моменты платежа внутри периода ренты. Виды финансовых рент Классификация рент может быть произведена по различным признакам. Рассмотрим их. В зависимости от продолжительности периода, ренты делят на годовые и p-срочные, где p - число выплат в году. Довольно часто в практике встречаются ренты, в которые период выплат превышает год и более (например, в инвестиционной деятельности). По числу начислений процентов различают ренты с начислением один в году, m раз или непрерывно. Моменты начисления процентов могут не совпадать с моментами рентных платежей. По величине членов различают постоянные (с равными членами)и переменные ренты. Если размеры платежей изменяются по какому-либо математическому закону, то часто появляется возможность вывести стандартные формулы, значительно упрощающие расчеты. По вероятности выплаты членов различают ренты верные и условные. Верные ренты подлежат безусловной выплате, например, при погашении кредита. Выплата условной ренты ставится в зависимость от наступления некоторого случайного события. Поэтому число ее членов заранее неизвестно. Например, число выплат пенсий зависит от продолжительности жизни пенсионера. По числу членов различают ренты с конечным числом членов или ограниченные и бесконечные или вечные. В качестве вечной ренты можно рассматривать выплаты по облигационным займам с неограниченными или не фиксированными сроками. Так, например, с необходимостью учета и расчета вечной ренты приходится сталкиваться при финансовых вычислениях, связанных с инвестированием денежных средств или покупкой финансового инструмента (материального объекта), если период их функционирования (возможного получения дохода) достаточно продолжительный и не оговорен конкретными сроками (отсюда и возможность получения бессрочной, т.е. «вечной» ренты), в качестве примера можно привести инвестирование в ценные бумаги крупнейших транснациональных компаний и государства (при отсутствии срока окончания их обращения), покупку доходных гостиниц, ферм, участков земли, производств и т.п. В зависимости от наличия сдвига момента начала ренты по отношению к началу действия контракта или какому-либо другому моменту ренты подразделяются на немедленные и отложенные или отсроченные. Срок немедленных рент начинается сразу, а у отложенных запаздывает. Ренты различают по моменту выплаты платежей. Если платежи осуществляются в конце каждого периода – года, полугодия, месяца и т.п., то такие ренты называются обычными или постнумерандо. Если же выплаты производятся в начале каждого периода, то ренты называются пренумерандо. Иногда предусматриваются платежи в середине каждого периода. постнумерандо(когда платежи осуществляются в конце соответствующих периодов) и ренты пренумерандо(когда соответствующие платежи осуществляются в начале указанных периодов). Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования. Рента пренумерандо отличается от обычной ренты числом периодов начисления процентов. Поэтому наращенная сумма ренты пренумерандо будет больше наращенной суммы обычной ренты в (1 + i) раз. Нечасто, но встречаются на практике и ренты, платежи по которым производятся в середине периодов. Такие ренты называются миннумерандо. Примером такой ренты могут служить, в ряде случаев, авансовые платежи по аренде помещений, а также полугодовые оплаты трат по внешнеторговым контрактам. Чаще всего в практических финансово-экономических расчетах решается, по существу, двуединая задача определения наращенной суммыили современной величины(стоимости) потока платежей. В данном контексте под современной величиной потока платежей понимается сумма всех его членов, дисконтированных на некоторый момент времени, совпадающий с началом потока платежей, или упреждающий его. Она может характеризовать капитализированный доход, чистую приведенную прибыль, приведенные издержки, эффективность инвестиций и валютно-финансовых условий внешнеторговых контрактов, доходность вкладов и депозитов и др. финансово-экономических и коммерческих операций. Формулы наращенной суммы Обычная годовая рента Пусть в конце каждого года в течение n лет на расчетный счет вносится по R рублей, проценты начисляются один раз в года по ставке i. В этом случае первый взнос к концу срока ренты возрастет до величины
где
Пример: В течение 3 лет на расчетный счет в конце каждого года поступает по 10 млн. руб., на которые начисляются проценты по сложной годовой ставке 10%. Требуется определить сумму на расчетном счете к концу указанного срока. Решение: Обычная годовая рента Пусть член годовой ренты равен R, процентная ставка i, проценты начисляются один раз в конце года, срок ренты n. Тогда дисконтированная величина первого платежа равна
Приведенная к началу ренты величина второго платежа равна Rn 2 и т.д. В итоге приведенные величины образуют геометрическую прогрессию: Rn, Rn 2,Rn 3,..., R nn, сумма которой равна
гд
|
||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.019 с.) |

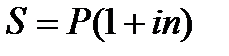 ,
, ,
, ,
,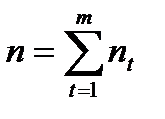 лет;
лет; ,
, (общий срок сделки);
(общий срок сделки); и
и  , т.е. когда периоды начисления и ставки процентов равны формула принимает
, т.е. когда периоды начисления и ставки процентов равны формула принимает ,
,

 получим (тыс. р.):
получим (тыс. р.): ;
; ;
; ;
; .
. ,
, ,
,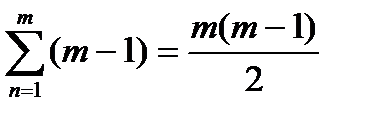 ,
, .
. ,
, .
. .
. .
. .
. ;
; .
.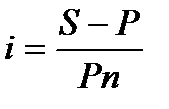 ,
, .
. ,
,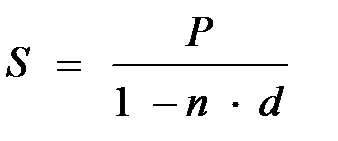
 .
.
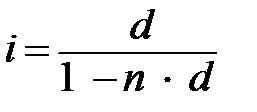 и
и  .
. и
и  .
. =
=  .
. и
и  .
. и
и  .
.
 0,285 9 или 28,59 %.
0,285 9 или 28,59 %. .
.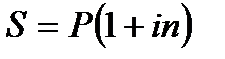 , а ее эквивалент в условиях инфляции равен
, а ее эквивалент в условиях инфляции равен  . Из равенства:
. Из равенства:  получаем:
получаем:  , где i – простая ставка процентов, характеризующая требуемую реальную доходность финансовой операции (нетто-ставка); i τ – процентная ставка с поправкой на инфляцию.
, где i – простая ставка процентов, характеризующая требуемую реальную доходность финансовой операции (нетто-ставка); i τ – процентная ставка с поправкой на инфляцию.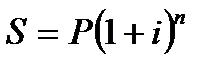 , а ее эквивалент в условиях инфляции равен
, а ее эквивалент в условиях инфляции равен  . Из равенства:
. Из равенства:  получаем:
получаем:  из которой можно сравнивать уровни процентной ставки и инфляции, проводить анализ эффективности вложений и устанавливать реальный прирост вложенного капитала.
из которой можно сравнивать уровни процентной ставки и инфляции, проводить анализ эффективности вложений и устанавливать реальный прирост вложенного капитала.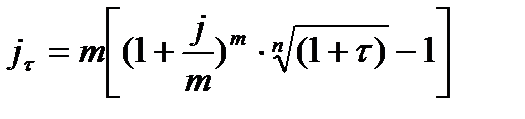 .
. ,
,  ,
,  .
. , R=0,32=32%
, R=0,32=32% или
или  , где
, где  -уровень инфляции.
-уровень инфляции. , рассчитывается по формуле:
, рассчитывается по формуле: 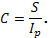
 . С учетом инфляции реальная стоимость суммы S составит
. С учетом инфляции реальная стоимость суммы S составит 
 .
. , здесь множитель наращения, учитывающий темп инфляции.
, здесь множитель наращения, учитывающий темп инфляции.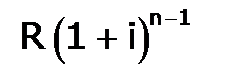 , так как на сумму R проценты начислялись в течение n-1 года. Второй взнос увеличится до
, так как на сумму R проценты начислялись в течение n-1 года. Второй взнос увеличится до  и т.д. На последний взнос проценты не начисляются. Таким образом, в конце срока ренты ее наращенная сумма будет равна сумме членов геометрической прогрессии
и т.д. На последний взнос проценты не начисляются. Таким образом, в конце срока ренты ее наращенная сумма будет равна сумме членов геометрической прогрессии , в которой первый член равен R, знаменатель (1+i), число членов n. Эта сумма равна
, в которой первый член равен R, знаменатель (1+i), число членов n. Эта сумма равна , (1.1)
, (1.1) - по схеме постнумерандо.
- по схеме постнумерандо.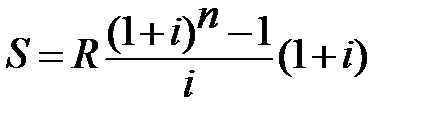 - по схеме пренумерандо. (1.2)
- по схеме пренумерандо. (1.2) млн. руб.
млн. руб.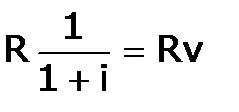 , где
, где  - дисконтный множитель.
- дисконтный множитель. , (1.7)
, (1.7)


