
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы исчисления простых процентовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ставка процентная - отношение процентных денег, уплаченных за единицу времени, к величине исходного капитала. Ставка учетная – отношение процентных денег, уплаченных за единицу времени, к ожидаемой к получению сумме денежных средств. Брутто-ставка – исходная базовая процентная ставка, указываемая в договорах. Доходность, выражаемая этой ставкой, не скорректирована на инфляцию. Ставка процентная положительная - любая ставка, при которой будет происходить реальное увеличение стоимости капитала при данном индексе инфляции. Ставка процентная реальная – процентная ставка, исчисляемая в условиях элиминирования влияния инфляции. Реальная ставка всегда меньше брутто-ставки. Ставка процентная постоянная – ставка, величина которой не меняется в течение времени начисления процентов. Ставка процентная переменная (плавающая) – процентная ставка, величина которой пересматривается в течение времени начисления процентов. Ставка процентная номинальная – годовая ставка сложных процентов, предусматривающая начисление процентов несколько раз в год. Ставка эффективная – годовая ставка сложных процентов, обеспечивающая тот же финансовый результат, что и начисление процентов несколько раз в год по номинальной ставке. Ставки эквивалентные – ставки, приводящие к одному финансовому результату при едином первоначальном капитале и сроке инвестирования. Наращение – это процесс увеличения суммы первоначального капитала за счет присоединения начисленных процентов. Процесс, в котором заданы исходная сумма и ставка, называется наращением, искомая величина – наращенной суммой, а ставка – ставкой наращения. Будущая стоимость – стоимость в некоторый момент времени, рассматриваемая с позиции будущего, при условии ее наращения по некоторой ставке. (Синоним – наращенная сумма.) Рассмотрим процесс наращения на основе простых и сложных процентных ставок.
Начисляем проценты по простой ставке один раз в год.
F – будущая стоимость, руб., P – первоначальный капитал, руб., r – простая процентная ставка, доли ед., n – количество периодов начисления, лет. F = P +I (5.2) I – сумма процентов, начисленная за n-ое количество лет, руб. (1+r*n) – множитель наращения
Множитель наращения – величина, показывающая, во сколько раз вырос первоначальный капитал.
Начисляем проценты по сложной процентной ставке один раз в год.
F – будущая стоимость, руб., P – первоначальный капитал, руб., r – сложная процентная ставка, доли ед., n – количество периодов начисления, лет. (1+r)n - множитель наращения
При начислении процентов на основе номинальной сложной процентной ставки установим новый параметр m – количество периодов начисления в течение года.
Определим эквивалентные ставки на основе сложной эффективной и сложной номинальной сложных процентных ставок.
В соответствии с принципом эквивалентности ставок F1= F2, P2= P2, n1= n2, следовательно,
Отсюда, возможно определение эффективной сложной процентной ставки
и номинальной сложной процентной ставки:
Аналогично можно реализовать принцип эквивалентности для любых ставок. Для учета инфляционного фактора используются ставки: rb – барьерная, rp – положительная, rd – брутто-ставка, rs – реальная.
Продемонстрируем учет инфляционного фактора на примере простой процентной ставки. Будущую стоимость с учетом инфляции можно определить на основе следующих формул:
а) с использованием брутто-ставки: Fi=P*[(1+rd*n)/Jp] (5.10) где Fi – будущая стоимость с учетом инфляции, руб., Jp – индекс цен за период сделки, доли ед.
б) либо с использованием реальной ставки: Fi=Р*(1+rs*n) (5.11)
Для оценки влияния инфляции на стоимость денежных средств выделим множитель наращения с учетом инфляции:
Если (1+rd*n) = Jp, то капитал сохраняется в первоначальном размере, т.е. ставка будет барьерной. Если (1+rd*n) < Jp, то происходит эрозия капитала. Если (1+rd*n) > Jp, то происходит реальное наращение денежных средств, т.е. стоимость капитала растет с учетом инфляции.
Барьерная ставка обеспечивает сохранение капитала в первоначальном размере при данном индексе цен, поэтому для ее определения воспользуемся следующей формулой: (1+rb*n) = Jp (5.13) следовательно,
Для расчета реальной и брутто-ставки вновь применим принцип эквивалентности ставок: [(1+rd*n)]/ Jp =(1+rs*n), отсюда
Аналогично определяются и сложные процентные ставки. Сохраним те же обозначения для сложных ставок для учета инфляции: rb – барьерная, rp – положительная, rd – брутто-ставка, rs – реальная. Определим будущую стоимость с учетом инфляции:
Множитель наращения, включающий брутто-ставку, с учетом инфляции будет выглядеть следующим образом:
Вновь рассчитаем - барьерную ставку
- брутто-ставку
- реальную ставку
Расчет брутто-ставки можно осуществить и по формуле Фишера (n=1):
rd = rs + h+ rs *h (5.23)
где h – темп инфляции за период начисления, доли ед.
Дисконтирование – процесс, обратный наращению, в котором заданы ожидаемая в будущем к получению (возращению) сумма и ставка. Современная стоимость – стоимость, найденная в процессе дисконтирования. Она характеризует величину, ожидаемую к получению в будущем, с позиции момента, к которому осуществляется дисконтирование. (Синонимы - приведенная, дисконтированная.) Принято выделять два способа дисконтирования: - математическое дисконтирование, - банковский учет (или учет векселей). Рассмотрим их последовательно. 1. Дисконтирование математическое P=F/(1+r*n) (5.25) 1/(1+r*n) – дисконтный множитель с простой процентной ставкой P=F/(1+r)n (5.26) 1/(1+r)n - дисконтный множитель со сложной процентной ставкой
Дисконтный множитель – величина, показывающая, во сколько раз уменьшается капитал при его дисконтировании. 2. Дисконтирование банковское (банковский учет, учет векселей) P=F*(1-d*n); (1-d*n) – дисконтный множитель с простой учетной ставкой, P=F*(1-d)n ; (1-d)n - дисконтный множитель со сложной учетной ставкой. D=F-P (5.27) где D – дисконт, руб.
Сложные учетные ставки также делятся на эффективные и номинальные.
Таблица 5.2
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 779; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.01 с.) |

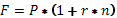 (5.1)
(5.1)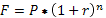 (5.3)
(5.3)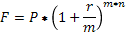 (5.4)
(5.4)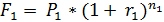 (5.5)
(5.5)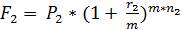 (5.6)
(5.6)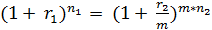 (5.7)
(5.7)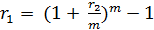 (5.8)
(5.8)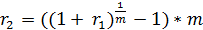 (5.9)
(5.9)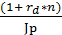 (5.12)
(5.12)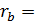
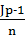 (5.14)
(5.14)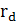 =
= 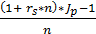 (5.15)
(5.15)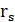 =
= 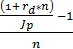 (5.16)
(5.16)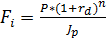 (5.17)
(5.17) (5.18)
(5.18)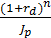
 (5.19)
(5.19) =
= 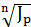 -1 (5.20)
-1 (5.20)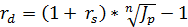 (5.21)
(5.21) =
=  (5.22)
(5.22)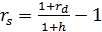 (5.24)
(5.24)


