
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постоянный аннуитет постнумерандо с начислением процентов m – раз за период.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если r является процентной ставкой за базовый период, а начисление сложных процентов происходит m раз в течение этого периода, то наращенный денежный поток, начиная с последнего денежного поступления, имеет вид:
Другими словами, мы получили геометрическую прогрессию, первый член которой равен А и знаменатель которой -
В рамках этой ситуации возможно решение двух задач: 1) используется для начисления схема сложных процентов; 2) используется схема простых процентов. Рассмотрим первую из них. Пусть в течение базового периода денежные поступления происходят p раз и один раз в конце периода начисляются сложные проценты в соответствии с ставкой r. На последнее поступление проценты не начисляются и оно остается равным А. На предпоследнее р – 1 поступление начисляются сложные проценты за часть периода 1/р и оно будет равно Поэтому будущая стоимость такого аннуитета будет определяться из выражения:
Поскольку Рассмотрим вторую задачу, полагающую, что на отдельные взносы, поступающие в течение периода, происходит начисление простых процентов. Для этого определим сумму, которая накопится к концу любого периода. Как и в предыдущем случае на последнее р-е поступление денежных средств проценты не начисляются и оно остается равным А. На предпоследнее поступление за период р – 1 начисляются простые проценты за 1/р - часть периода и оно будет равно Аналогичным образом предшествующее (р –2) – е поступление станет равным Полученные величины образуют арифметическую прогрессию (разность равна; число членов р), следовательно сумма членов такой прогрессии будет равна:
Таким образом, имеем дело с аннуитетом, в котором денежные поступления в каждом периоде равны величине Для определения будущей стоимости такого аннуитета используется формула:
Рассмотрим самую общую ситуацию, когда в течение базового периода денежные поступления происходят р раз и проценты начисляются m за период. Здесь возможны две ситуации: либо начисляются простые проценты, либо - сложные. Если происходит начисление только сложных процентов, то, как и ранее, определяем вначале сумму, образовавшуюся в конце любого периода. Последнее поступление в периоде остается равным А, т.к. на него не производится начисление процентов. Предпоследнее поступление после начисления сложных процентов составит
Будущая стоимость аннуитета с денежными поступлениями, равными полученной сумме, определяется по формуле:
Пример. Вам предлагается сдать в аренду участок с арендной платой в размере 5 тыс. грн. в конце каждого полугодия. При этом возможно начисление процентов: а) ежегодное; б) полугодовое; в) ежеквартальное. Какой из вариантов предпочтительнее?
а) ежегодное начисление процентов. Возможно либо начисление сложных, либо простых процентов. Будущая стоимость аннуитета при начислении сложных процентов:
Если в течение года начисляются простые процента, то будущая стоимость аннуитета составит:
б) начисление процентов по полугодиям:
в) ежеквартальное начисление процентов:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.255.58 (0.007 с.) |

 .
.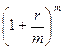 . Следовательно, сумма первых n членов этой прогрессии будет равна:
. Следовательно, сумма первых n членов этой прогрессии будет равна:

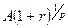 . На р – 2 поступление начисляются сложные проценты на часть периода 2/р и оно будет равно
. На р – 2 поступление начисляются сложные проценты на часть периода 2/р и оно будет равно  и т.д. до первого денежного поступления включительно, которое будет равно
и т.д. до первого денежного поступления включительно, которое будет равно  . Полученная последовательность величин представляет собой геометрическую прогрессию с первым членом А, знаменателем
. Полученная последовательность величин представляет собой геометрическую прогрессию с первым членом А, знаменателем 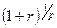 и числом членов, равным р.
и числом членов, равным р. , или
, или 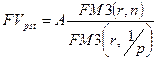 .
. , значения
, значения  в финансовых таблицах как правило не приводятся. Поэтому для расчета коэффициента наращения такого аннуитета пользуются формулой:
в финансовых таблицах как правило не приводятся. Поэтому для расчета коэффициента наращения такого аннуитета пользуются формулой:  .
.
 и т.д. Наконец, первое поступление будет равняться
и т.д. Наконец, первое поступление будет равняться  .
.
 .
.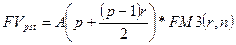 .
.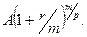 Предшествующее ему
Предшествующее ему  поступление -
поступление -  и т. д. вплоть до первого, которое станет равным
и т. д. вплоть до первого, которое станет равным  Сумма полученных величин составит:
Сумма полученных величин составит:



 тыс. грн.
тыс. грн. тыс. грн.
тыс. грн.


