
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование сложной учетной ставки в процессах наращения и дисконтирования по схеме сложных процентов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим ситуацию предварительного начисления сложных процентов, т.е. когда сложный процент начисляется в момент заключения финансового соглашения. Такая ситуация может иметь место при покупке дорогостоящих товаров в кредит, или при продаже некоторого финансового инструмента до срока его погашения. В этом случае осуществляется операция дисконтирования и применяется сложная учетная ставка. Предположим, что некоторое долговое обязательство на сумму FV и сроком погашения через n продается (учитывается) раньше срока с дисконтом по сложной учетной годовой ставке d. Если долговое обязательство продается за n лет до срока, то продавец получит сумму
где множитель Таким образом, PV представляет собой текущую (современную) стоимость будущего платежа FV. Дисконт равен величине
Пример. Долговое обязательство на выплату 20 тыс. грн. со сроком погашения 4 года учтено за 2 года до срока с дисконтом по сложной учетной ставке 8% годовых. Найти величину дисконта.
Если срок, за который осуществляется дисконтирование, не является целым числом лет, то возможны следующие методы определения стоимости учтенного капитала: Ø использование сложной учетной ставки:
Ø использование смешанной схемы:
где w – целое число лет; f - дробная часть года.
Пример. Долговое обязательство на выплату 20 тыс. грн. со сроком погашения 4 года учтено за 27 месяцев до срока с дисконтом по сложной учетной ставке 8% годовых. Найти величину дисконта.
Если сравнивать между собой дисконтирование по простой и сложной учетным ставкам, то, для лица, осуществляющего предварительное (антисипативное) начисление процентов: Ø более выгодным является дисконтирование по сложной учетной ставке, если срок учета менее одного года; Ø более выгодным является дисконтирование по простой учетной ставке, если срок учета превышает один год; Ø дисконтирование в обоих случаях дает один и тот же результат, если срок учета равен одному году. Если дисконтирование происходит m раз в году и задана сложная годовая учетная ставка d, то определение стоимости капитала, учтенного за n лет при m–кратном дисконтировании в течение года определяется по формуле:
Пример. Долговое обязательство на выплату 3 тыс. грн. со сроком погашения 5 лет учтено за 2 года до срока. Определить полученную сумму, если производилось: а) полугодовое; б) поквартальное дисконтирование по номинальной учетной ставке 12% годовых. а) б)
Если антисипативное начисление процентов (или дисконтирование) осуществляется по внутригодовым подпериодам, но общий период не равен целому числу подпериодов, то для этой цели используются следующие формулы:
Пример. Определить современное значение суммы в 4 тыс. грн., если они будут выплачены через 2 года и 3 месяца и дисконтирование производилось по полугодиям по номинальной годовой учетной ставке 10%. Полагаем n = 2,25, m = 2, w = 2*2,25 = 4,5 = 4, f = 4,5 – 4 = 0,5.
Если необходимо определить время до срока погашения долгового обязательства, то используются следующие формулы:
Пример. За долговое обязательство в 30 тыс. грн. банком было выплачено 20 тыс. грн. За какое врямя до срока погашения было учтено это обязательство, если банком использовалась годовая сложная учетная ставка 8%?
Если необходимо определить величину номинальной учетной ставки при известных значениях остальных параметров финансовой операции, то необходимо пользоваться формулами:
Пример. Вексель был учтен за полтора года до срока, при этом владелец векселя получил 0,8 от написанной на векселе суммы. По какой сложной годовой учетной ставке был учтен вексель? Поскольку PV = 0,8FV, то Часто встречаются ситуации, когда условиями контракта предусматриваются плавающие учетные ставки. Пусть на периоды времени
Обозначим Таким образом, на все время можно установить вместо плавающих учетных ставок среднюю учетную ставку, которая обеспечит такой же результат. Вышеприведенной формулой можно пользоваться и в случае, когда периоды времени выражены в различных единицах при условии согласования их размерностей с размерностями соответствующих учетных ставок. Пример. Вклад в размере 1000 грн. положен в банк сроком на 7 лет, причем предусмотрен следующий порядок начисления сложных процентов по плавающей учетной ставке: в первые два года – 8%, в последующие 4 года – 12%, а в оставшийся год – 15%. Найти наращенную сумму.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |


 называется дисконтным множителем.
называется дисконтным множителем.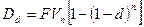
 тыс. грн.
тыс. грн.  тыс. грн.
тыс. грн.

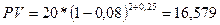 тыс. грн.
тыс. грн. тыс. грн.
тыс. грн.
 тыс. грн.
тыс. грн. тыс. грн.
тыс. грн.
 или
или 
 тыс. грн.
тыс. грн.  тыс.грн.
тыс.грн. или, если m=1
или, если m=1 
 года
года , или, если m=1
, или, если m=1 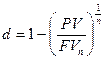
 или 13,82%.
или 13,82%. установлены сложные учетные ставки соответственно
установлены сложные учетные ставки соответственно  . Тогда при наращении сложными процентами итоговая сумма за время
. Тогда при наращении сложными процентами итоговая сумма за время 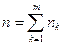 (если все периоды времени измеряются в одних единицах) определяется по формуле:
(если все периоды времени измеряются в одних единицах) определяется по формуле: .
. , тогда формула для определения наращенной суммы примет вид:
, тогда формула для определения наращенной суммы примет вид:  .
. грн.
грн.


