
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погашение долга равными срочными уплатами.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Условиями кредитного контракта может предусматриваться погашение долга равными срочными уплатами в конце каждого расчетного периода. Каждая срочная уплата (A) будет являться суммой двух величин: годового расхода по погашению основного долга (R) и процентного платежа по займу (I), т.е.: A = R + I В этом случае остаток основного долга и суммы процентных платежей уменьшаются от периода к периоду, годовой расход погашенного основного долга растет, а срочные уплаты будут являться аннуитетом ренты постнумерандо. Следовательно, величина кредита PV, будет равняться сумме всех дисконтированных аннуитетов, т.е. является современной величиной всех срочных уплат:
где r - ставка процентов по займу. Умножив выражение (1) на величину (1 + r), получим:
Если вычесть из выражения (2) выражение (1), и проделать необходимые преобразования, то получим:
Из выражения (3) можно получить величину срочной уплаты: Величина
Пример. Банк выдал кредит в сумме 40 тыс. грн. на 5 лет под 6% годовых. Погашение кредита должно производиться равными ежегодными выплатами в конце каждого года, включающими погашение основного долга и процентные платежи. Начисление процентов производится раз в году. Необходимо составить план погашения долга. Ежегодная выплата будет составлять:
За первый год величина процентного платежа составит:
Так как А = R + I, то выплата основного долга определится величиной:
Остаток основного долга после первого года составит:
Процентный платеж во втором году будет равняться:
Величина выплаты основного долга во втором году составит:
Изложенная процедура повторяется до конца срока погашения долга. Итоговая расчетная таблица погашения долга представлена ниже.
Рассмотренная методика составления плана погашения займа равными платежами не является единственной. Рассмотрим некоторые другие. При погашении займа равными платежами остаток долга с каждой выплатой уменьшается, следовательно, уменьшаются и процентные выплаты. В результате возрастает от периода к периоду размер платежей, идущих на погашение основного долга (см. табл.). Между двумя последовательными выплатами основного долга существует взаимосвязь. Для ее определения возьмем два последовательных расчетных периода – k и (k +1) –й. В k-м расчетном периоде годовая срочная уплата составит:
а остаток невыплаченного долга соответственно определяется как
Однако для определения
следовательно, срочная уплата в этом периоде может быть записана в виде следующего выражения:
По условию
То есть каждая выплата, произведенная в счет погашения основного долга, отличается от предыдущей на величину Зная эту зависимость, можно рассчитать величину выплаты основного долга в любом расчетном периоде. Так Зная размер кредита Величина займа
После некоторых преобразований данного выражения величину
В этой формуле величина Пример. Для условий ранее рассмотренного примера рассчитать величину первого и четвертого платежа для погашения основного долга.
Размер платежа основного долга в любом периоде Известно, что первая выплата определяется выражением: а величина кредита равняется:
Подставив значение PV в формулу расчета величины первого платежа, получим:
Так как или
Используя выражение (6), можно рассчитать для любого периода величину процентного платежа Так как, Подставим в это выражение значение
Пример. Для условий ранее рассмотренного примера рассчитать величину первого платежа и величину процентного платежа на конец последнего года погашения займа.
Для расчета остатка невыплаченного основного долга на любой момент времени воспользуемся выражением:
Подставив в это выражение значения
Пример. По данным ранее рассмотренного примера рассчитать остаток основного невыплаченного долга на начало 3-го года погашения.
Для определения размера годовой срочной уплаты можно воспользоваться также методом депозитной книжки. Суть метода депозитной книжки заключается в следующем. Рассуждая с позиции кредитора, для банка рассматриваемый контракт будет представлять инвестицию в размере 40 тыс. грн., т.е. отток денежных средств. В дальнейшем в течение 5 лет банк будет ежегодно в конце года получать сумму А, которая будет включать проценты за истекший год и часть основной суммы долга. Таким образом, мы имеем дело с аннуитетом постнумерандо, о котором известны его текущая стоимость, процентная ставка и продолжительность действия. Поэтому для нахождения величины годового платежа воспользуемся финансовыми таблицами и формулой:
Для
План погашения долга при изменяющейся процентной ставке. Финансовыми контрактами часто предусматриваются условия, когда на протяжении финансовой сделки процентная ствка не является постоянной, а изменяется от периода к периоду. Вышерассмотренная методика может быть использована и для решения таких финансовых задач.
Пример. Предприятием получен кредит в сумме 100 млн. грн. Сроком на 7 лет. Процентная ставка по годам изменяется следующим образом.
План погашения долга приведен в таблице.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1653; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.65.133 (0.006 с.) |

 (1)
(1)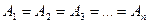 - срочные уплаты;
- срочные уплаты; (2)
(2) (3)
(3)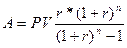 или
или 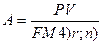 (4)
(4) называется коэффициентом погашения задолженности.
называется коэффициентом погашения задолженности.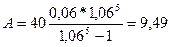 тыс. грн.
тыс. грн.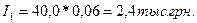
 тыс. грн.
тыс. грн.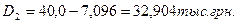
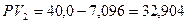 тыс. грн.
тыс. грн.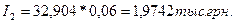
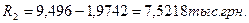
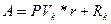
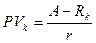
 необходимо предварительно определить
необходимо предварительно определить 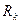 . В периоде (k + 1) остаток основного долга составит:
. В периоде (k + 1) остаток основного долга составит: ,
,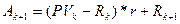 .
. , значит
, значит  . Решив это уравнение относительно
. Решив это уравнение относительно 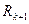 , получим:
, получим: . (5)
. (5)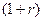 . Зная эту зависимость можно рассчитать величину выплаты основного долга в любом расчетном периоде.
. Зная эту зависимость можно рассчитать величину выплаты основного долга в любом расчетном периоде.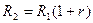 ;
; 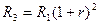 , и т.д.
, и т.д.  .
. , процентную ставку
, процентную ставку  и срок погашения кредита
и срок погашения кредита  , рассчитаем величину первой выплаты погашения основного долга
, рассчитаем величину первой выплаты погашения основного долга 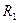 .
.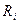 , т.е.:
, т.е.: .
. .
.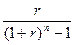 называется ставкой погашения.
называется ставкой погашения.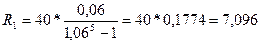 тыс.грн.
тыс.грн.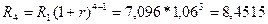 тыс. грн.
тыс. грн. можно определить не только по формуле (5), но и другим способом.
можно определить не только по формуле (5), но и другим способом. .
.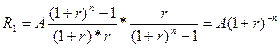 .
.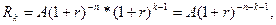
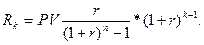 (6)
(6)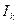 .
.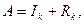 то
то  .
.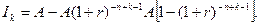
 тыс. грн.
тыс. грн.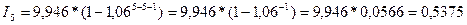 тыс. грн.
тыс. грн.
 и
и 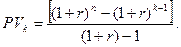
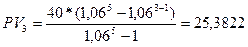 тыс. грн.
тыс. грн.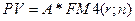 .
.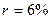 и
и 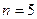 лет значение FM4 будет равняться 4,2124. Значит искомая величина аннуитета составит 40: 4,2124 = 9,4958 тыс. грн.
лет значение FM4 будет равняться 4,2124. Значит искомая величина аннуитета составит 40: 4,2124 = 9,4958 тыс. грн.


