
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погашение долга единовременным платежомСодержание книги
Поиск на нашем сайте
Количественный анализ долгосрочной задолженности (займа) применяется для достижения сбалансированности, т.е. адекватности его параметров принятым условиям финансового соглашения, путем планирования погашения долга. Планирование погашения долга заключается в определении периодических расходов, связанных с займом, – такие расходы называются обслуживанием долга. Разовая сумма обслуживания долга – срочная уплата, в которую входят: · текущие процентные платежи; · средства, для погашения (амортизации) основной суммы долга. Размеры срочных уплат зависят от условий займа: · срока; · наличия и продолжительности льготного периода; · уровня процентной ставки; · способа погашения основной суммы долга и выплаты процентов. Для кредитной схемы в качестве исходных параметров выступают величина займа (D), срок его погашения (n), процент по кредиту (i), под который выдаются деньги, и поток платежей по выплате долга (Yt). Рассмотрим различные способы погашения задолженности, поскольку от выбора способа погашения стоимость кредита (сумма выплачиваемых процентов) будет различной. Здесь возможны два варианта: а) погашение единовременным платежом, т.е. возврат всей суммы в оговоренный срок; б) погашение долга в рассрочку, т.е. частями.
3.1.1. Погашение основной суммы долга единовременным платежом в конце срока с постоянной выплатой процентов. Рассмотрим погашение единовременным платежом. В простейшем случае кредит погашается единым платежом в конце срока:
Y = D • (1 + i) n,
где Y – срочная уплата; D – сумма долга. Этот платеж, как наращенная сумма долга, состоит из двух частей: · возврат основной суммы долга (D); · выплата процентов по долгу (I), где I = D • (1 + i) n - D. В финансовой практике встречаются случаи, когда у кредитора возникает необходимость вернуть часть денег досрочно. В таких случаях возникает риск невозврата, поскольку требуемой суммы на такой момент времени может и не быть. При значительной сумме долга разовый платеж требует создания так называемого фонда погашения, путем периодических взносов. Фонд погашения аккумулирует денежные средства, направленные на погашение задолженности. Наиболее эффективно размещение фонда погашения с начислением на взносы процентов, например, на специальном счете в банке. Не трудно заметить, что такие платежи по своей сути являются финансовой рентой (аннуитетом), поэтому задача сводится к определению одного из параметров финансовой ренты – члена ренты. Здесь возможно два варианта. Первый – выплата процентов по мере их начисления, а основная сумма денег возвращается в конце срока займа.
Если проценты выплачиваются ежегодно, тогда величина срочной уплаты (расходов должника по погашению долга) равна:
где D – первоначальная сумма долга; q – ставка процентов по условиям займа; sn; i – коэффициент наращения финансовой ренты; n – срок долга в годах; i – ставка процентов при создании фонда погашения. Здесь фигурируют две ставки процентов: i – определяет скорость роста суммы фонда погашения; q – сумму выплачиваемых за заем процентов.
Пример. Долг 100 тыс. долларов выдан под 10% годовых на 3 года, с ежегодной выплатой процентов по долгу. Для погашения суммы долга единовременным платежом создается фонд, куда ежегодно вносятся равные суммы, на которые начисляются проценты по ставке 11%. Найти ежегодные расходы должника. Решение: Ежегодные расходы должника составляют величину срочной уплаты: Y = I + R, I = D • q = 100'000 • 0,1 = 10'000 долларов,
Отсюда Y = 10'000 + 29'921,31 = 39'921,31 долларов. Таким образом, ежегодные расходы должника по обслуживанию долга составят 39'921,31 долларов. Однако, более наглядным и эффективным способом планирования долга является составление таблиц, в которых отражают все основные характеристики обслуживания долга: План погашения долга единовременным платежом с ежегодной выплатой процентов и созданием погасительного фонда
Таким образом, из приведенной таблицы видно, что ежегодные расходы по обслуживанию долга составят 39'921,31 долларов, что в целом за три года составит сумму 119'763,93 долларов, причем выплата процентов за три года 30'000 долларов, а на погашение основного долга в размере 100'000 долларов приходится всего лишь 89'763,93 долларов, т.е. 10'236,07 долларов является набежавшими процентами на размещенные средства в фонде погашения. Таким образом, создание фонда погашения является необходимым элементом составления плана погашения долга, т.к. позволяет не только снизить риск не возврата денежных средств, но и сократить расходы по обслуживанию суммы долга.
3.1.2. Погашение основной суммы долга и процентов по нему единовременным платежом в конце срока ссуды. Второй вариант погашения долга единовременным платежом состоит в выплате процентов одновременно с погашением долга.
В этом случае взносы в фонд погашения являются одновременно и величиной срочной уплаты (членом финансовой ренты):
где D – первоначальная сумма долга; q – ставка процентов по условиям займа; sn; i – коэффициент наращения финансовой ренты; n – срок долга в годах; i – ставка процентов при создании погасительного фонда.
Пример. Рассмотрим предыдущий пример, изменив условия: погашение единовременным платежом, как суммы основного долга, так и выплаты процентов. Решение: Величина срочной уплаты равна: Y = [ D • (1 + q) n ]: Sn; i = 100'000 • (1 + 0,11) • 3: 3,3421000 = 39'825,26 долларов Таким образом, величина ежегодных расходов по обслуживанию долга составит 39'825,26 долларов, что несколько меньше аналогичного показателя в предыдущем примере, следовательно, меньше и общая сумма расходов по обслуживанию долга, составляющая величину 119'475,78 долларов. Для более наглядного представления плана погашения долга здесь также необходимо составление таблицы. План погашения долга единовременным платежом
Как видно из таблицы, происходит ежегодное увеличение суммы долга за счет присоединения к нему процентов, поэтому к концу срока долг возрастет до 133'100 долларов, из которых выплата процентов составит 33'100 долларов. Однако за счет увеличения размера взносов в погасительный фонд общая величина обслуживания долга уменьшается. Погашение долга в рассрочку
В практике финансовой деятельности долг часто погашается в рассрочку, т.е. распределенными во времени платежами. При погашении основной суммы долга частями его текущее значение будет уменьшаться и, следовательно, сумма процентных платежей также будет уменьшаться. Погашение долга частями также может осуществляться различными способами. В зависимости от преследуемых интересов стороны могут выбирать различные, удобные для них режимы в виде постоянных или переменных финансовых рент, а также нерегулярных потоков платежей.
3. 2.1. Погашение основной суммы долга равными частями. Одним из вариантов погашения долга в рассрочку является погашение основной суммы долга равными частями. При этом величина погашения долга определяется следующим образом:
dt = D: n = const, где dt – величина погашения основной суммы долга; D – первоначальная сумма долга; n – срок долга в годах; t – номер года, t = 1, 2, …, n. Проценты начисляются на уменьшаемую сумму основного долга: It = Dt • q, где Dt – остаток долга на начало очередного года; q – ставка процентов, начисляемых на сумму долга. Тогда размер срочной уплаты можно представить как сумму процентов и сумму погашения долга:
Yt = It + dt, где Yt – срочная уплата на конец текущего года. Пример. Сумма 100 тыс. долларов выдана под 10% годовых на 3 года. Определить величину срочной уплаты при погашении основной суммы долга равными ежегодными частями. Решение: Величина суммы погашения долга равна: dt = D: n = 100'000: 3 = 33'333,33 доллара. Поскольку величина срочной уплаты при таком способе погашения долга меняется из года в год, то в этом случае без построения плана погашения долга в виде таблицы просто не обойтись. План погашения основной суммы долга равными частями
Таким образом, общие расходы по обслуживанию долга составили 120 тыс. долларов, из которых 20 тыс. долларов составляют проценты, а 100 тыс. долларов – погашение основной суммы долга. [2]
3.2.2. Погашение долга и процентов по нему равными суммами в течение срока ссуды. Долг также можно погашать в рассрочку равными срочными уплатами, которые включают в себя как погашение основной суммы долга, так и величину процентов по нему:
Yt = It + dt = const. При погашении долга в рассрочку величина долга систематически убывает, что приводит к уменьшению процентов и, соответственно, увеличению сумм, идущих на погашение долга, – это так называемое прогрессивное погашение. Поскольку срочные уплаты равны, то их последовательность представляет собой финансовую ренту, современное значение которой должно быть равно сумме долга. По формуле для определения размера платежа постоянной годовой финансовой ренты с выплатами в конце периода, размер срочной уплаты равен:
где Yt – величина срочной уплаты; D – первоначальная сумма долга; q – процентная ставка на сумму долга; n – срок долга в годах; t – номер года, t = 1, 2, …, n.
Пример. Условия предыдущей задачи, но погашение долга предусматривает уплату равными срочными выплатами. Решение: Срочная уплата, включающая в себя погашение основной суммы долга и выплату процентов по долгу, равна: Yt = 100'000,00: 2,486851991 = 40'211,48 долларов. Отсюда общие расходы по погашению долга равны: Σ Yt = 40'211,48 • 3 = 120'634,44 доллара. Таким образом, ежегодные расходы по погашению долга будут составлять 40'211,48 долларов, а за весь срок финансовой операции – 120'634,44 доллара. При этом варианте погашения долга также возможно построение таблицы. План погашения долга равными срочными уплатами
Таким образом, общие расходы по обслуживанию долга составляют 120'634,44 долларов, из которых 100 тыс. долларов идут на погашение долга, а 20'634,44 долларов – проценты. В таблице наглядно представлено распределение суммы срочной уплаты на выплату процентов и непосредственное погашение долга. Потребительский кредит Частным случаем погашения долга равными срочными уплатами является потребительский кредит, при котором проценты начисляются сразу на всю сумму кредита, а сумма задолженности равномерно погашается на протяжении всего срока кредита. Проценты в потребительском кредите начисляются сразу на всю сумму долга по простой ставке: I = D • n • i Тогда общая сумма расходов по погашению кредита складывается из выплаты процентов и суммы основного долга: Σ Yt = D + I Следовательно, размер срочной уплаты определяется по формуле: Σ Yt = (D + I): (n • m), где n – срок кредита в годах; m – количество взносов в течение года.
Пример. Потребительский кредит на сумму 5 тыс. руб. открыт на 2 года по ставке 25% годовых. Погашение кредита равными взносами ежеквартально. Определить стоимость кредита и размер ежеквартальных взносов. Решение: Стоимость кредита – это проценты, которые равны: I = D • n • i = 5'000 • 2 • 0,25 = 2'500 рублей Общая сумма расходов по обслуживанию кредита равна: Σ Yt = D + I = 5'000 + 2'500 = 7'500 рублей Ежеквартальные взносы составят величину: Σ Yt = (D + I): (n • m) = 7'500: 2 • 4 = 937,50 рублей Таким образом, ежеквартальные взносы в размере 937,50 рублей позволяет выплатить сумму долга и выплатить проценты. Если бы использовалось прогрессивное погашение, т.е. начисление процентов на остаток долга, то это было бы заметно дешевле для должника. Расчленение величины срочной уплаты в потребительском кредите на процентные платежи и погашение основной суммы долга в мировой практике называется "методом 78". Это связано с тем, что для потребительского кредита сроком 12 месяцев и ежемесячным погашение, сумма порядковых номеров месяцев будет равна 78, что и дало название такому методу начисления процентов. Это правило можно обобщить для n лет и m платежей в году:
N = m • n [(m • n + 1): 2], где N – сумма последовательных номеров выплат. Отсюда очень легко расчленить срочную уплату на процентные платежи и сумму погашения основного долга: Yt = It + dt, где It – процентный платеж; dt – сумма погашения основного долга. Тогда величина процентного платежа определяется следующим образом:
It = I • (t / N), а сумма погашения основного долга как разница срочной уплаты и процентных выплат:
Rt = Yt - It. Рассмотрим предыдущий пример, расчленив срочную уплату на составляющие элементы, все данные представив в виде таблицы. План погашения потребительского кредита
Примеры решения задач ЗАДАЧА 1 При открытии счета по ставке простого процента 20% годовых 20.01.2000 на счет положена сумма 5000 рублей. С 01.03.2000 ставка процентов по вкладу 18% годовых. 01.06.2000 на счет положена сумма 10000 рублей. С 01.08.2000 ставка процентов по вкладу 14% годовых. 30.10.2000 счет закрыт. Найти полученную сумму, используя точные и обычные проценты. Решить задачу также с учетом проведения операции реинвестирования 01.05.2000. Решение: Изобразим описанную ситуацию на оси времени: отметим даты изменения условий финансовой операции и рассчитаем соответствующие временные промежутки, используя обычные простые проценты.
Определим полученную сумму, используя обычные проценты:
До 01.06 проценты начисляются на сумму 5000 руб, а с 01.06 на сумму 15000 руб. Определим полученную сумму, используя точные проценты:
Определим полученную сумму, при реинвестировании капитала 01.05.2000, используя обычные проценты: На оси времени покажем момент реинвестирования.
ЗАДАЧА 2. Предприятие продало товар, получив вексель номинальной стоимостью $1000, сроком 75 дней и процентной ставкой 15% (проценты не входят в номинальную стоимость). Через 60 дней с момента оформления векселя предприятие решило учесть его в банке; предложена ставка 16%. Рассчитать суммы, получаемые банком и предприятием.
Решение: Сумма, получаемая банком:
Сумма, получаемая предприятием:
ЗАДАЧА 3. Сложные проценты на вклады начисляются ежеквартально по номинальной ставке 10% годовых. Определить сумму процентов, начисленных на вклад 200 тыс. руб. за 2 года. Найти эффективную ставку.
Решение:
Эффективную ставку определим из равенства
Тогда
ЗАДАЧА 4. Предприятие приобрело здание за $15000 на следующих условиях: а) 30% стоимости оплачивается немедленно; б) оставшаяся часть погашается равными годовыми платежами в течение 8 лет с начислением 15% годовых на непогашенную часть кредита по схеме сложных процентов. Определить общую сумму процентов к выплате. Составить схему погашения. Решение: При оплате 30% от стоимости здания начальный долг предприятия будет равен Обозначим через А величину годового платежа. Поток этих платежей представляет собой аннуитет постнумерандо, для которого PVpst=$10500, r=15%, n=8 лет. Поэтому для нахождения величины А воспользуемся формулой
Выразив А из уравнения, получим Составим схему погашения долга в виде таблицы. (
Как видно из таблицы, общая сумма процентов к выплате составит $8218,98. ЗАДАЧА 5. Первоначальный капитал в размере 20 млн. руб. выдается на три года, проценты начисляются в конце каждого квартала по номинальной ставке 8% годовых. Определить барьерную и брутто-ставку, обеспечивающую доходность в 8% годовых, если ожидаемый годовой уровень инфляции составляет 12%. Решение: Зная уровень инфляции Н=12%, определим ее индекс по формуле: I = H + 1 I = 0,12 + 1 = 1,12. Проценты начисляются по схеме сложного процента 4 раза в год (в конце каждого квартала). Определим покупательную способность наращенной суммы S(T). Для этого поделим ее на индекс инфляции I(T).
Найдем барьерную ставку из уравнения, сохраняющего покупательную способность начальной суммы в условиях инфляции (покупательная способность S(0) сохраниться, если коэффициент наращения будет равен 1):
Поскольку длительность операции 3 года, индекс инфляции за этот период I(T)=1,123=1,405. Тогда Для определения брутто-ставки, обеспечивающей наращение капитала 8% годовых при инфляции, воспользуемся формулой Фишера: Тогда ЗАДАЧА 6 На годовые взносы пренумерандо по $1000 банк каждые полгода в течение 5 лет начисляет ежеквартально проценты по ставке 12% годовых. Какая сумма будет на счете в конце срока? Решение: Рента является постоянной, р-срочной, пренумерандо. Сумму наращенного капитала можно определить из формулы для расчета наращенной суммы аналогичной ренты, только постнумерандо.
Для пренумерандо формула примет вид:
Тогда
ЗАДАЧА 7 Два аннуитета с параметрами: 1.величина платежа - $2000, ставка процента - 8% годовых, срок - 12 лет; 2.величина платежа - $4000, ставка процента - 10% годовых, срок - 10 лет требуется заменить одним – со сроком 10 лет и процентной ставкой 5% годовых.
Решение: Определим современную стоимость каждого аннуитета.
Общая современная стоимость аннуитетов будет равна
Тогда годовой платеж для этого аннуитета с процентной ставкой 5% и сроком 10 лет определим из уравнения
А = $5134,74 Литература. 1.Ковалев В.В. Уланов В.А. Курс финансовых вычислений. М.: Финансы и статистика, 1999. 2.Финансовый менеджмент/ под ред. Стояновой Е.С. М.: Перспектива,1998. 3.Малыхин В.И. Финансовая математика. М.: ЮНИТИ,1999 4.Финансовый менеджмент/ под ред. Стояновой Е.С. М.: Перспектива,1998. 5.Малыхин В.И. Финансовая математика. М.: ЮНИТИ,1999 6.Четыркин Е.М. Методы финансовых и коммерческих расчетов. М.:Дело,1992.
Вопросы к экзамену для группы ЭиУПП 1.Понятие модели и моделирования. 2.Классификация моделей по средствам моделирования. 3.Использование средств моделирования в экономических исследованиях. 4.Особенности математического моделирования экономических процессов. 5.Общий вид математических моделей и основные направления их исследования. 6.Оптимизационный подход к исследованию ЭММ. 7.Методы многокритериальной оптимизации. 8.Имитационные эксперименты и имитационные системы. 9.Классификация экономико–математических моделей 10. Простейшая финансовая операция. Ее параметры и их взаимосвязь. 11. Понятие операций наращения и дисконтирования. Антисипативный и декурсивный метод. 12. Наращение по простым декурсивным процентам (понятие простых процентов, различные варианты начисления по простым процентам). Обычные и точные проценты. 13. Наращение по декурсивным сложным процентам. Различные схемы наращения. 14. Сравнение схем наращения по простым и сложным процентам. 15. Эффективная ставка процентов, ее вычисление и применение. 16. Дисконтирование и его виды (понятие операции дисконтирования, виды дисконтирования). 17. Математическое дисконтирование 18. Банковский учет. 19. Понятие потока платежей, параметры потока платежей. 20. Классификация потоков платежей. 21. Вечная рента. Определение современной стоимости вечной ренты. 22. Нахождение наращенной суммы постоянных рент постнумерандо (вывод формулы для любого типа ренты). 23. Нахождение современной стоимости постоянных рент постнумерандо (вывод формулы для любого типа ренты). 24. Ренты пренумерандо. Вычисление наращенной и приведенной стоимости рент пренумерандо. Связь с аналогичными суммами рент постнумерандо. 25. Потоки платежей с неравными поступлениями. 26. Двусторонние потоки платежей и их характеристика (чистая приведенная величина, ставка доходности). 27. Эффективная ставка для простейшей финансовой операции и внутренняя норма доходности. 28. Кредитные расчеты (выплата долга за один раз в конце срока, выплата долга равными суммами) 29. Выплата долга равными срочными уплатами, переменными срочными уплатами 30. Потребительский кредит. Расчеты по потребительскому кредиту. Вопросы по теме «Эконометрика» 1. Введение в эконометрику. 1. Понятие эконометрики. Области применения эконометрики. 2. Случайные переменные. Генеральная совокупность и выборка. Основные характеристики случайных величин. 3. Понятие связи между переменными. Функциональная и стохастическая связи экономических данных. 4. Основные виды эконометрических моделей. 5. Основные этапы построения эконометрической модели. 6. Исходные данные для построения эконометрической модели. 7. Основные требования к исходным данным. Модель парной регрессии 1. Модель парной регрессии: описание модели, виды моделей. 2. Сущность метода наименьших квадратов. 3. Понятие статистической значимости результата. Проверка на статистическую значимость. 4. Определение доверительного интервала. 5. Статистическая значимость параметров парной регрессии 6. Интервальные оценки параметров регрессии. Геометрическая интерпретация. 7. Расчет коэффициента детерминации. Оценка качества построенной модели с помощью коэффициента детерминации. 8. Проверка соответствия модели выборочным данным с помощью теста Фишера. 9. Проверка точности модели. 10. Предсказание по линейной модели парной регрессии. Точечный прогноз. Стандартная ошибка точечного прогноза. Интервальный прогноз Модели временных рядов 1. Понятие временного ряда. Основные требования к данным временных рядов. Основные задачи моделирования временных рядов. 2. Структура временного ряда. Понятие тренда, сезонных и циклических колебаний. 3. Метод Фостера – Стюарта выявления тенденции. 4. Проверка качества модели временного ряда на основе исследования ряда остатков. 5. Критерии проверки случайности ряда остатков: критерий поворотных точек, критерий серий. 6. Понятие автокорреляции. Причины появления автокорреляцию Методы выявления автокорреляции. 7. Критерий Дарбина– Уотсона. 8. Проверка выполнения нормального распределения в случайном ряду. 9. Прогнозирование на основе трендовой модели.
ЛИТЕРАТУРА 1. Бородич С.А. Эконометрика. Минск.: Новое знание, 2001 2. Д. Джонстон. Эконометрические методы. — М.: Статистика, 1980. 3. Доугерти К. Введение в эконометрику. — М.: ИНФРА-М, 1997. 4. Замков О.О., Толстопятенко А.В. Математические методы в экономике. М.: ДИС,1997 5. Лиогонький М.И., Мамаева З.М. Эконометрика.(Учебное пособие). Нижний Новгород:ННГАСУ, 2003 (http://mamaeva.alterxp.com/plog/) 6. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. — М.: Дело, 1997. 7. Мамаева З.М. Эконометрика. Методическое пособие. Нижний Новгород: УРАО, 2004 (http://mamaeva.alterxp.com/plog/) 8. Носко В.П. Эконометрика для начинающих. — М. ИЭПП, 2000 (http://www.iet.ru)/ 9. Эконометрика./под ред Елисеевой И.И.. М.:Финансы и статистика, 2001 Литература по финансовым расчетам 1. Ковалев В.В. Уланов В.А. Курс финансовых вычислений. М.: Финансы и статистика, 1999. 2. Финансовый менеджмент/ под ред. Стояновой Е.С. М.: Перспектива,1998. 3. Малыхин В.И. Финансовая математика. М.: ЮНИТИ,1999 4. Финансовый менеджмент/ под ред. Стояновой Е.С. М.: Перспектива,1998. 5. Малыхин В.И. Финансовая математика. М.: ЮНИТИ,1999 6. Четыркин Е.М. Методы финансовых и коммерческих расчетов. М.:Дело,1992.
[1] Сравните полученные результаты с выплатой долга единовременным платежом. [2] Сравните полученные результаты с выплатой долга единовременным платежом.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 4883; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.255.63 (0.01 с.) |









 40 дн
40 дн
 руб.
руб. руб.
руб.

 18%
18%

 30 дн
30 дн
 60 дн
60 дн


 руб.
руб. $
$ $
$ тыс.руб.
тыс.руб.
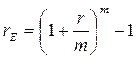

 $
$
 $
$
 =
= 

 , так как предполагается одинаковйй годовой уровень инфляции в течении всего срока операции.
, так как предполагается одинаковйй годовой уровень инфляции в течении всего срока операции.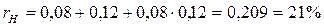
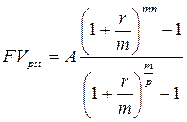

 $
$ $
$ $
$ $
$



