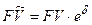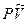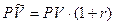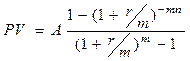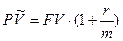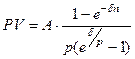Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Методический материал для выполнения контрольной работы (тема 2)Содержание книги
Поиск на нашем сайте
Простейшие финансовые операции. Наращение капитала. Параметры операции:; T– длительность финансовой операции (измеряется в годах), r–годовая ставка ссудного процента; d– учетная ставка (ставка дисконта) PV -величина инвестиции (суммы, отданной в долг под проценты); FV– наращенная сумма в конце финансовой операции Если в операции наращения используется ставка ссудного процента r, то метод называется декурсивным, если используется учетная ставка d– антисипативным. 1.1.1. Наращение капитала по простым процентам (декурсивный метод):
а) б) При ежегодно изменяющейся ставке: в) При ставке, меняющейся в разные периоды: где n – продолжительность финансовой операции, г) При нецелом числе лет: Обычно при определении продолжительности проведения операции даты ее начала и окончания считаются за 1 день. Возможны три варианта начисления: 1.Точные проценты: точная продолжительность периода t и база T=366 или 365 дней (английский вариант). 2. Обыкновенные проценты: приблизительная продолжительность периода t (считается, что в месяце 30 дней) и база T=360дней(германский вариант) 3.Смешенный вариант (французский): точная продолжительность периода t и база T=360дней. 1.1.2. Наращение капитала по сложным процентам (декурсивный метод): а) начисление процентов один раз в году: б) начисление процентов m раз в году: в) Если срок инвестиций не является целым числом, тогда
Эффективная ставка Определение: годовая ставка сложных процентов, дающая то же соотношение между выданной суммой PV и суммой FV, что и при любой схеме выплат называется эффективной. а) Общий случай: б) наращение по сложным процентам с начислением m раз в году: Для каждой схемы расчетов можно определить свою эффективную ставку Наращение капитала на основе антисипативного метода a) начисление процентов 1 раз в году по простым процентам: Очевидно, что должно выполняться условие: b) начисление процентов за период менее года(либо при не целом Т): c) начисление по сложным процентам 1 раз в году: d) начисление по сложным процентам m раз в году: Дисконтирование В финансовой практике часто сталкиваются с задачей обратной наращению процентов: по заданной сумме FV, которую следует уплатить через время T; необходимо определить сумму получаемой ссуды PV Параметры операции: T– длительность финансовой операции (измеряется в годах), r–годовая ставка ссудного процента; d– учетная ставка (ставка дисконта) PV -современная стоимость будущей суммы FV; Математическое дисконтирование (применяется ставка ссудного процента –r) а) по схемее простого процента: б) по схеме сложного процента с начислением один раз в году: в) по схемее сложного процента с начислением m раз в году: Банковский (коммерческий учет). (Применяется схема дисконтирования с использованием учетной ставки d.) a) Простые проценты: b) Сложные проценты с начислением 1 раз в году: c) Сложные проценты с начислением m раз в году: 1.5. Определение параметров (r, T,d) простейшей финансовой операции Для определения ставки ссудного процента, учетной ставки или срока проведения операций необходимо воспользоваться формулами наращения или дисконтирования, из которых находится искомый параметр.
Потоки платежей (аннуитеты) Поток платежей, все элементы которого распределены во времени так, что интервалы между любыми двумя последовательными платежами постоянны, называют финансовой рентой или аннуитетом (annuity). Ренты характеризуются следующими параметрами: A– член ренты, т.е. величина каждого годового платежа, p - число платежей в году, m– число начислений процентов в году, T– срок ренты в годах (время от начала ренты до конца последнего периода выплат). t –период ренты (временной интервал между двумя последовательными платежами, r–годовая ставка процента; FV– наращенная сумма (сумма всех членов потока платежей с начисленными на них к концу срока процентами); PV– приведенная (современная) стоимость потока платежей–это сумма всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени Если платежи осуществляются в конце периода, имеем ренту постнумерандо, в начале периода– пренумерандо. Если платежи осуществляются равномерно в течении периода, то считают, что платеж приурочен к середине периода, а ренту называют равномерной. Основные формулы наращения
Отличие постоянных рент пренумерандо от рент поснумерандо состоит в том, что время начисления процентов на каждую выплату увеличивается на один период ренты, следовательно, сумма наращения Это же правило сохраняется и для приведенных стоимостей указанных рент
Основные формулы приведения
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.164.176 (0.01 с.) |



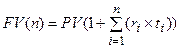 ,
,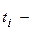 продолжительность действия ставки
продолжительность действия ставки  .
. , где t – длительность операции в днях, K – длительность года в днях
, где t – длительность операции в днях, K – длительность года в днях ;
;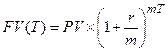 ;
; , где целое чисто лет [T], а {T} – часть срока сверх целого числа лет (в годах):
, где целое чисто лет [T], а {T} – часть срока сверх целого числа лет (в годах):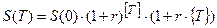
 ;
;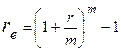 .
.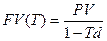
 , т.е.
, т.е. 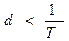 .
.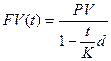
 .
.

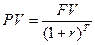
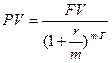
 . В этой схеме чаще всего используется способ точных процентов.
. В этой схеме чаще всего используется способ точных процентов.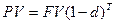
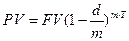
 PV и FV в этом случае заданы.
PV и FV в этом случае заданы.




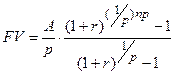
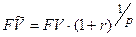

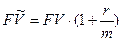
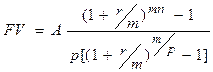
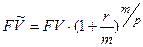
 )
)