
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра экономики народного хозяйстваСодержание книги Поиск на нашем сайте
Кафедра экономики народного хозяйства
З.М. Мамаева
Контрольные задания по курсу «Экономико-математическое моделирование» и методические указания к их выполнению
Нижний Новгород, 2011
Задания контрольной работы по теме 1 «Эконометрическое моделирование» Задание 1 · Построить модель парной регрессии, определяющую зависимость между объемом выпуска продукции Y (в тыс. руб.) и затратами труда X (в чел/днях). · Оценить качество построенной модели. · Построить точечный и интервальный прогноз для Х=Х0
Задание 2. Построить линейную модель множественной регрессии, используя Пакет анализа таблиц EXCEL. Объяснить результаты · .
Задание 3
1 Значения показателя Y в задании 1 являются уровнями временного ряда. Проверить наличие тренда в этом ряду. Выбрать и построить трендовую модель. Провести оценку ее качества Теоретический материал и методические указания к решению следует смотреть в у чебно – методическом пособии по эконометрике Задания для выполнения контрольной работы по теме 2. ВАРИАНТ 1 1. При открытии счета при ставке 18% годовых 01.01.2010 на счет положена сумма 10000 руб. С 1.06.2010 ставка процентов по вкладу 16% годовых. 10.09.2010 со счета снята сумма 2000 руб. С 01.10.2010 ставка процентов по вкладу 15% годовых. 30.12 2010 вклад закрыт. Найти полученную сумму, используя обычные и точные проценты. Решить задачу также с учетом проведения операции реинвестирования 01.06.2000. 2. Оценить рост цен за год при темпах инфляции 5% в первый квартал, 8% во второй, 7% в третий и 10% в последний. Определить простую годовую и сложную ежеквартальную барьерные банковские ставки процентов. Определить простую годовую и сложную ежеквартальную брутто-ставки процентов, которые обеспечат реальную доходность по вкладам банка 12% за год. .3. Первоначальная сумма капитала на 01.01.1998 1000 д.е. Какой будет капитал на 01.01.2000, если начисление процентов будет выполняться ежемесячно при номинальной ставке 36% годовых? Определить эффективную ставку процентов. Определить эквивалентную номинальную ставку процентов с начислением процентов по полугодиям. 4.. Составить план погашения долга в размере 3000 д.е. со ставкой процентов по займу 12% годовых за 6лет равными срочными уплатами в конце каждого года. Имеется льготный двухлетний период, в котором кредитору выплачиваются проценты, но основной долг не погашается.
ВАРИАНТ 2 1. При открытии счета при ставке 20% годовых 01.01.2010 на счет положена сумма 20000 руб. С 1.02.2010 ставка процентов по вкладу 18% годовых. 01.05.2010 со счета снята сумма 5000 руб. С 01.06.2010 ставка процентов по вкладу 15% годовых. 06.08.2010 счет закрыт. Найти полученную сумму, используя обычные и точные проценты. Решить задачу также с учетом проведения операции реинвестирования 01.06.2010 и с добавлением на счет 4000 руб. . 2. Определить срок платежа по векселю на сумму 1000 д.е., если при его учете по номинальной учетной ставке 36% годовых с дисконтированием по полугодиям получена ссуда 800 д.е. При необходимости выполнить коррекцию дисконта так, чтобы срок был с целым количеством дней (из расчета 360 дней в году). 3. Первоначальная сумма капитала на 01.01.2001 10000 руб. Каков будет капитал на 05.08.2001, если начисление процентов будет выполняться по полугодиям при номинальной ставке 18% годовых? Определить Эффективную ставку процентов. Определить эквивалентную номинальную ставку процентов с начислением процентов поквартально. 4.. Для погашения через 5 лет долга 1500 д.е. со ставкой процентов по займу 24% годовых формируется фонд из взносов должника в конце каждого года на специальный счет банка при номинальной ставке 18% годовых с ежемесячным начислением процентов, чтобы в нем к концу срока займа накопилась сумма основного долга. В конце каждого года проценты по сумме основного долга выплачиваются кредитору. Составить план ежегодных расходов заемщика на погашение долга.
Вариант 3. 1. При открытии счета при ставке 20% годовых 20.01.2009 на счет положена сумма 5000руб. С 1.03.2010 ставка процентов по вкладу 18% годовых. 01.06. 2010 на счет положена сумма 10000 руб. С 01.08. 2010 ставка процентов по вкладу 14% годовых. 30.10.2010 счет закрыт. Найти полученную сумму, используя точные и обычные проценты. Решить задачу также с учетом проведения операции реинвестирования1.05.2010. 2. Первоначальная сумма капитала на 01.01.2001 10000 руб. Каков будет капитал на 01.01.2002, если проценты начисляются 2 раза в год по ставке 18% годовых? Определить эффективную ставку процентов и эквивалентную номинальную ставку с начислением процентов ежемесячно. 3. Определить срок платежа по векселю на сумму 2мл. руб., если при его учете по учетной ставке 25% годовых получена ссуда 1,8мл. руб. Выполнить коррекцию дисконта так, чтобы срок был с целым количеством днейю 4. На банковском счете накапливается фонд 6000 д.е. с помощью постоянных взносов в начале каждого квартала по 400 д.е. На поступившие взносы начисляются 12% каждые полгода. Найти срок накопление с целым количеством кварталов. При необходимости выполнить коррекцию: а) всех взносов, б) последнего взноса.
Вариант 4 1. При открытии счета при ставке 18% годовых 5.10. 2009на счет положена сумма 10000 руб. С 01.01. 2010 ставка процентов по вкладу 14% годовых. 10.02. 2010 а счет добавлена сумма 3000 руб. С 01.02. 2010 ставка процентов по вкладу 12% годовых. Найти сумму вклада, используя обычные и точные простые проценты на 01. 06. 2010. Какая будет сумма, если 10.02. 2010 провести операцию реинвестирования. 2. Предприятие продало товар, получив вексель номинальной стоимостью $15000, сроком 150 дней.. Через 60 дней с момента оформления векселя предприятие решило учесть его в банке; предложенная ставка 16%. Рассчитайте суммы, • получаемые банком и предприятием. 3. Сложные проценты на вклады начисляются ежеквартально по номинальной годовой ставке 100% годовых. Определить сумму процентов, начисленных на вклад 200 тыс. руб. за 2 года. Найти эффективную ставку. 4. Оценить рост цен за год при темпах инфляции 4% в первый квартал, 5% во второй, 4% в третий и 5% в последний. Определить простую годовую и сложную ежемесячную барьерные банковские ставки процентов. Определить простую годовую и сложную ежемесячную брутто-ставки процентов, которые обеспечат реальную доходность по вкладам банка 2% в месяц. Вариант 5 . При открытии счета при ставке 25% годовых 10.02. 2009 на счет положена сумма 15000 руб. С 01.03. 2009 ставка процентов по вкладу 22% годовых. 10.05. 2009 со счета снята сумма 5000 руб. С 20.06. 2009 ставка процентов по вкладу 20% годовых. 20.09. 2009 счет закрыт. Найти полученную сумму, используя обычные и точные простые проценты. Найти сумму вклада на 20.09. 2009, если 10.05. 2009 проведена операция реинвестирования. 2. Долговое обязательство на выплату 20000руб. со сроком погашения 4 года учтено через 2 года с дисконтом по сложной учетной ставке 15%.Определить величину дисконта. 3. Оценить рост цен за год при темпах инфляции 6% в первый квартал, 9% во второй, 5% в третий и 10% в последний. Определить простую годовую и сложную ежеквартальную барьерные банковские ставки процентов. Определить простую годовую и сложную ежемесячную брутто-ставки процентов, которые обеспечат реальную доходность по вкладам банка 8% за год. 4. На банковском счете накапливается фонд 6000 д.е. с помощью постоянных взносов в начале каждого года по 1200 д.е. На поступившие взносы начисляются 2% ежемесячно. Найти срок накоплений с целым количеством лет. При необходимости выполнить коррекцию: а) всех взносов, б) последнего взноса. Вариант 6 1. При открытии счета при ставке 25% годовых 10.01.2009 на счет положена сумма 10000 руб. С 01.06.2009 ставка процентов по вкладу 20% годовых. 10.06. 2009 со счета снята сумма 5000 руб. С 15.07. 2009 ставка процентов по вкладу 18% годовых. 20.10. 2009 счет закрыт. Найти полученную сумму, используя точные и обычные простые проценты. Решить задачу также с учетом закрытия старого счета и открытия нового 10.06. 2009 на полученную сумму с вычетом 5000 руб. 2. Банк ежеквартально начисляет сложные проценты на вклады по ставке 25% годовых. Определить сумму, которую надо положить в банк, чтобы через 3 года накопить 100 млн. руб. 3. Определить срок платежа по векселю на сумму 10000 руб., если при его учете по номинальной учетной ставке 24% годовых с дисконтированием поквартально получена ссуда 8000руб. При необходимости выполнить коррекцию дисконта так, чтобы срок был с целым количеством дней (из расчета 360 дней в году). 4. Составить план погашения долга в размере 1500 д.е. со ставкой процентов по займу 24% годовых за 5 лет равными долями в конце каждого года.
Вариант 7
1.При открытии счета при ставке 25% годовых 20.03.2009 на счет положена сумма 10000 руб. С 16.05.2009 ставка процентов по вкладу 20% годовых. 20.05.2009 со счета снята сумма 5000 руб. С 16.07.2009 ставка процентов по вкладу 15% годовых. 20.02.2010 счет закрыт. Найти полученную сумму, используя английский, французский и германский способы начисления процентов. Решить задачу также с учетом закрытия старого счета и открытия нового 20.05.2009 на полученную сумму с вычетом 5000руб. 2. Определить срок платежа по векселю на сумму 1000 д.е., если при его учете по номинальной учетной ставке 36% годовых с дисконтированием поквартально получена ссуда 920 д.е. При необходимости выполнить коррекцию дисконта так, чтобы срок был с целым количеством дней (из расчета 365 дней в году). 3.. Оценить рост цен за год при темпах инфляции 10% в полугодие. Определить простую годовую и сложную ежеквартальную барьерные банковские ставки процентов. Определить простую годовую и сложную ежеквартальную брутто-ставки процентов, которые обеспечат реальную доходность по вкладам банка 3% в квартал. 4. Для погашения через 3 года долга 2500 д.е. со ставкой процентов по займу 18% годовых формируется фонд из взносов должника в начале каждого года на специальный счет банка с ежемесячным начислением 2%, чтобы в нем к концу срока займа накопилась сумма основного долга. В конце каждого года проценты по сумме основного долга выплачиваются кредитору. Составить план ежегодных расходов заемщика по погашению долга.
3.ВАРИАНТ 8
1. При открытии счета при ставке 12% годовых 25.05.2009 на счет положена сумма 20000 руб. С 15.07. 2009 ставка процентов по вкладу 10% годовых. 20.07. 2009на счет добавлена сумма 5000 руб. С 01.08. 2009 ставка процентов по вкладу 8% годовых. 25.04.2010 счет закрыт. Найти полученную сумму, используя английский, французский и германский способы начисления процентов. Решить задачу также с учетом закрытия старого счета и открытия нового 20.07.2009на полученную сумму с добавлением 5000 руб. 2. Первоначальный капитал на 01.01.1998 1000 д.е. Каков будет капитал на 01.01.2001, если начисление процентов будет выполняться с использованием полугодовой ставки 4%? Определить эффективную ставку процентов. Определить эквивалентную номинальную ставку процентов с начислением процентов ежемесячно. 3. На банковском счете в течение 5 лет накапливается фонд с помощью постоянных взносов в конце каждого года по 200 д.е. На поступившие взносы начисляются 2% ежемесячно. Найти размер накопленного фонда. 4. Определить срок платежа по векселю на сумму 1000 д.е., если при его учете по номинальной учетной ставке 16% годовых с дисконтированием поквартально получена ссуда 900 д.е. При необходимости выполнить коррекцию дисконта так, чтобы срок был с целым количеством дней (из расчета 365 дней в году).
ВАРИАНТ № 9 1. При открытии счета при ставке 20% годовых 10.01. 2009 на счет положена сумма 10000 руб. С 15.02. 2009 ставка процентов по вкладу 15% годовых. 11.03. 2009 со счета снята сумма 5000 руб. С 15.04. 2009 ставка процентов по вкладу 10% годовых. 20.04.2010 счет закрыт. Найти полученную сумму, используя английский, французский и германский способы начисления процентов. Решить задачу также с учетом закрытия старого счета и открытия нового 11.03. 2009 на полученную сумму с вычетом 5000 руб. 2. Первоначальный капитал на 01.01.1998 — 1000 д.е. Каков будет капитал на 01.01.2001, если начисление процентов будет выполняться с использованием поквартальной ставки 4%? Определить эффективную ставку процентов. Определить эквивалентную номинальную ставку процентов с начислением процентов по полугодиям. 3. Для получения постоянной ренты в течение 5 лет с выплатами в начале каждого года по 800 д.е. на специальный счет банка были вложены средства при номинальной годовой ставке 8% годовых с начислением процентов ежемесячно. Найти размер вклада. 4. Оценить рост цен за год при темпах инфляции 3% в месяц, Определить простую годовую и сложную ежеквартальную барьерные банковские ставки процентов. Определить простую годовую и сложную ежеквартальную брутто-ставки процентов. ВАРИАНТ № 10 1. При открытии счета при ставке 10% годовых 11.01. 2009 на счет положена сумма 10000 руб. С 15.03. 2009 ставка процентов по вкладу 15% годовых. 21.03. 2009 на счет добавлена сумма 5000 руб. С 15.04. 2009ставка процентов по вкладу 10% годовых. 20.04.2010 счет закрыт. Найти полученную сумму, используя английский, французский и германский способы начисления процентов. Решить задачу также с учетом закрытия старого счета и открытия нового 21.03. 2009 на полученную сумму с добавлением 5000 руб. 2. Первоначальный капитал на 01.01.1998 — 1000 д.е. Каков будет капитал на 01.01.2001, если начисление процентов будет выполняться с использованием поквартальной ставки 5% годовых? Определить эффективную ставку процентов. Определить эквивалентную номинальную ставку процентов с ежемесячным начислением процентов. 3. Составить план погашения долга в размере 1500 д.е. со ставкой процентов по займу 30% годовых за 5 лет равными срочными уплатами в конце каждого года. 4. Для получения постоянной ренты в течение 5 лет с выплатами в начале каждого года по 800 д.е. на специальный счет банка были вложены средства при номинальной годовой ставке 8% годовых с начислением процентов ежемесячно. Найти размер вклада. Наращение капитала. Параметры операции:; T– длительность финансовой операции (измеряется в годах), r–годовая ставка ссудного процента; d– учетная ставка (ставка дисконта) PV -величина инвестиции (суммы, отданной в долг под проценты); FV– наращенная сумма в конце финансовой операции Если в операции наращения используется ставка ссудного процента r, то метод называется декурсивным, если используется учетная ставка d– антисипативным. 1.1.1. Наращение капитала по простым процентам (декурсивный метод):
а) б) При ежегодно изменяющейся ставке: в) При ставке, меняющейся в разные периоды: где n – продолжительность финансовой операции, г) При нецелом числе лет: Обычно при определении продолжительности проведения операции даты ее начала и окончания считаются за 1 день. Возможны три варианта начисления: 1.Точные проценты: точная продолжительность периода t и база T=366 или 365 дней (английский вариант). 2. Обыкновенные проценты: приблизительная продолжительность периода t (считается, что в месяце 30 дней) и база T=360дней(германский вариант) 3.Смешенный вариант (французский): точная продолжительность периода t и база T=360дней. 1.1.2. Наращение капитала по сложным процентам (декурсивный метод): а) начисление процентов один раз в году: б) начисление процентов m раз в году: в) Если срок инвестиций не является целым числом, тогда
Эффективная ставка Определение: годовая ставка сложных процентов, дающая то же соотношение между выданной суммой PV и суммой FV, что и при любой схеме выплат называется эффективной. а) Общий случай: б) наращение по сложным процентам с начислением m раз в году: Для каждой схемы расчетов можно определить свою эффективную ставку Дисконтирование В финансовой практике часто сталкиваются с задачей обратной наращению процентов: по заданной сумме FV, которую следует уплатить через время T; необходимо определить сумму получаемой ссуды PV Параметры операции: T– длительность финансовой операции (измеряется в годах), r–годовая ставка ссудного процента; d– учетная ставка (ставка дисконта) PV -современная стоимость будущей суммы FV; Потоки платежей (аннуитеты) Поток платежей, все элементы которого распределены во времени так, что интервалы между любыми двумя последовательными платежами постоянны, называют финансовой рентой или аннуитетом (annuity). Ренты характеризуются следующими параметрами: A– член ренты, т.е. величина каждого годового платежа, p - число платежей в году, m– число начислений процентов в году, T– срок ренты в годах (время от начала ренты до конца последнего периода выплат). t –период ренты (временной интервал между двумя последовательными платежами, r–годовая ставка процента; FV– наращенная сумма (сумма всех членов потока платежей с начисленными на них к концу срока процентами); PV– приведенная (современная) стоимость потока платежей–это сумма всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени Если платежи осуществляются в конце периода, имеем ренту постнумерандо, в начале периода– пренумерандо. Если платежи осуществляются равномерно в течении периода, то считают, что платеж приурочен к середине периода, а ренту называют равномерной. Основные формулы наращения
Отличие постоянных рент пренумерандо от рент поснумерандо состоит в том, что время начисления процентов на каждую выплату увеличивается на один период ренты, следовательно, сумма наращения Это же правило сохраняется и для приведенных стоимостей указанных рент
Основные формулы приведения
Основные понятия Важным практическим приложением теории аннуитетов является составление различных вариантов (планов) погашения задолженности, Анализ задолженности включает: · Разработку план погашения займа. · Оценку стоимости долга на любой момент времени. · Анализ эффективности финансовой операции для кредитора и заёмщика Планирование погашения долга заключается в определении периодических расходов, связанных с займом, – такие расходы называются обслуживанием долга. Разовая сумма обслуживания долга – срочная уплата, в которую входят: · текущие процентные платежи; · средства, для погашения (амортизации) основной суммы долга. Размеры срочных уплат зависят от условий займа: · срока; · наличия и продолжительности льготного периода; · уровня процентной ставки; · способа погашения основной суммы долга и выплаты процентов.
Все эти параметры оговаривают при заключении контракта Для кредитной схемы в качестве исходных параметров выступают следующие показатели: · D–основная сумма долга (без процентов), · r–ставка процента по займу, · I– процент по займу (процентные деньги); · A – размер взноса на погашение задолженности; · Y– величина срочной уплаты, Y=А+Y; · Варианты погашения задолженности
Можно выделить пять основных вариантов погашения задолженности: 1. Займы без обязательного погашения 2. Погашение долга в один срок 3. Погашение долга равными суммами 4. Погашение долга с использованием постоянных срочных уплат 5. Погашение долга с использованием переменных срочных уплат. Рассмотрим эти случаи 1. Займы без обязательного погашения. В данном случае речь идет о вечной ренте. Задача в данном случае заключается и нахождении размера выплачиваемой суммы A при заданной процентной ставке r. Современная стоимость аннуитета: 9.2.1. Погашение долга единовременным платежом в конце срока Если заемщик должен вернуть всю сумму долга в конце срока, целесообразным бывает создание погасительного (амортизационного) фонда (например, депозит банка), для чего периодически в фонд вносятся определенные суммы, на которые начисляются проценты. Если процентная ставка, под которую вносятся средства, не превышает размеров ставки, под которую выдается заем, создание погасительного фонда не имеет смысла. Выгоднее сразу расплачиваться этими суммами с кредитором. Создание погасительного фонда может оговариваться в контракте в качестве гарантии. Пусть Взносы в погасительный фонд зависят от методов уплаты процентов по займу: a) Проценты по займу уплачиваются кредитору регулярно. Найдем величину срочной уплаты Y и ее составляющих (Y=P+I). По определению I=D×r. Регулярные взносы в погасительный фонд может рассматривать как определенную ренту. Например, рассмотрим ренту годовую постоянную ренту постнумерандо. Сумма, накопленная в погасительном фонде за n лет, т. е. наращенная сумма аннуитета с параметрами A, n, g, должна составить величину D. Используем формулу суммы ренты: D Величина срочной уплаты в данном случае определяется формулой: Следует сказать, что платежи в погасительный фонд могут быть представлены рентой любого типа, соответственно будет меняться формула наращенной суммы.
b). Проценты по займу не выплачиваются, а присоединяются к сумме долга. Если проценты не выплачиваются, а присоединяются к основной сумме долга, то срочная уплата будет состоять только из взносов в погасительный фонд, обозначим их Общая сумма долга на конец срока составит величину
Пример. Долг 90 тыс. долларов выдан под 10% годовых на 3 года, с ежегодной выплатой процентов по долгу. Для погашения суммы долга единовременным платежом создается фонд, куда ежегодно вносятся равные суммы, на которые начисляются проценты по ставке 12%. Найти ежегодные расходы должника. Решение: Ежегодные расходы должника составляют величину срочной уплаты: Y = I + A, I = D • q = 90'000 • 0,1 = 9'000 долларов,
А
Отсюда Y = 10'000 + 29'921,31 = 39'921,31 долларов. Таким образом, ежегодные расходы должника по обслуживанию долга составят 39'921,31 долларов. Однако, более наглядным и эффективным способом планирования долга является составление таблиц, в которых отражают все основные характеристики обслуживания долга: План погашения долга единовременным платежом с ежегодной выплатой процентов и созданием погасительного фонда
Таким образом, из приведенной таблицы видно, что ежегодные расходы по обслуживанию долга составят 39'921,31 долларов, что в целом за три года составит сумму 119'763,93 долларов, причем выплата процентов за три года 30'000 долларов, а на погашение основного долга в размере 100'000 долларов приходится всего лишь 89'763,93 долларов, т.е. 10'236,07 долларов является набежавшими процентами на размещенные средства в фонде погашения. Таким образом, создание фонда погашения является необходимым элементом составления плана погашения долга, т.к. позволяет не только снизить риск не возврата денежных средств, но и сократить расходы по обслуживанию суммы долга.
Пример. Рассмотрим предыдущий пример, изменив условия: погашение единовременным платежом, как суммы основного долга, так и выплаты процентов. Решение: Величина срочной уплаты равна: Y = [ D • (1 + q) n ]: Sn; i = 100'000 • (1 + 0,11) • 3: 3,3421000 = 39'825,26 долларов Таким образом, величина ежегодных расходов по обслуживанию долга составит 39'825,26 долларов, что несколько меньше аналогичного показателя в предыдущем примере, следовательно, меньше и общая сумма расходов по обслуживанию долга, составляющая величину 119'475,78 долларов. Для более наглядного представления плана погашения долга здесь также необходимо составление таблицы. План погашения долга единовременным платежом
Как видно из таблицы, происходит ежегодное увеличение суммы долга за счет присоединения к нему процентов, поэтому к концу срока долг возрастет до 133'100 долларов, из которых выплата процентов составит 33'100 долларов. Однако за счет увеличения размера взносов в погасительный фонд общая величина обслуживания долга уменьшается. Погашение долга в рассрочку
В практике финансовой деятельности долг часто погашается в рассрочку, т.е. распределенными во времени платежами. При погашении основной суммы долга частями его текущее значение будет уменьшаться и, следовательно, сумма процентных платежей также будет уменьшаться. Погашение долга частями также может осуществляться различными способами. В зависимости от преследуемых интересов стороны могут выбирать различные, удобные для них режимы в виде постоянных или переменных финансовых рент, а также нерегулярных потоков платежей.
Погашение основной суммы долга равными частями. Одним из вариантов погашения долга в рассрочку является погашение основной суммы долга равными частями. При этом величина погашения долга определяется следующим образом: Аt = D: n = const, где Аt – величина погашения основной суммы долга; D – первоначальная сумма долга; n – срок долга в годах; t – номе
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.214.1 (0.01 с.) |



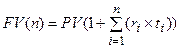 ,
,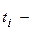 продолжительность действия ставки
продолжительность действия ставки  .
. , где t – длительность операции в днях, K – длительность года в днях
, где t – длительность операции в днях, K – длительность года в днях ;
;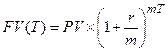 ;
; , где целое чисто лет [T], а {T} – часть срока сверх целого числа лет (в годах):
, где целое чисто лет [T], а {T} – часть срока сверх целого числа лет (в годах):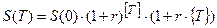
 ;
;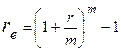 .
.




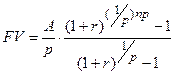
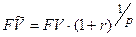

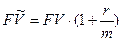
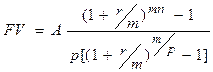
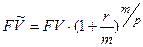
 )
)

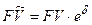


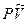

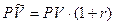
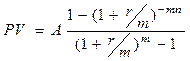


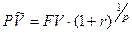

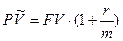




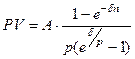
 –срок займа
–срок займа , отсюда размер платежа
, отсюда размер платежа  .
. –ставка процентов в погасительном фонде.
–ставка процентов в погасительном фонде. , Отсюда
, Отсюда  .
.
 .
.
 , откуда получаем:
, откуда получаем: =
= 





