
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наращение денежных средств по простым и сложным про- центамСодержание книги
Поиск на нашем сайте
1. Процентный доход или проценты – это абсолютный доход от предоставления долга.
тала. где - будущая стоимость капитала, - текущая стоимость капи-
Сложные проценты характеризуются тем, что база начисления рас- тет в результате регулярного присоединения к ней (капитализации) про- центных денег, причитающихся кредитору за предыдущие расчетные пе-
Начисление процентов при использовании переменной процентной ставки Основная формула сложных процентов предполагает постоянную процентную ставку на протяжении всего срока начисления процентов. Од- нако нестабильность экономической ситуации вынуждает кредиторов ис-
соответствующие ставки.
правилах ряда коммерческих банков для некоторых операций в этих слу- чаях проценты начисляются только за целое число лет. В большинстве случаев учитывается полный срок. При начислении процентов при дробном числе лет ссуды использу- ется два основных метода расчета: 1) начисление по схеме сложных процентов. В этом случае в течение всего срока ссуды начисляются сложные проценты:
2) смешанный метод предполагает начисление процентов за целое число лет по формуле сложных процентов, а за дробную часть периода – по формуле простых процентов:
Эффективная годовая процентная ставка – процентный доход, получаемый инвестором за один год в результате вложения одной денеж-
Реальная процентная ставка – это процентная ставка, очищенная от инфляции.
2. Дисконтирование – это приведение всех денежных потоков (по- токов платежей) к единому моменту времени. Приведение к моменту времени в прошлом называют дисконтирова- нием.
Приведение к моменту в будущем называют наращением (компаун- дированием). Исследуя целесообразность финансовых вложений, инвестор должен оценить, какими будут его доходы в будущем, какую максимально воз-
можную сумму допустимо вложить в данное дело, исходя из прогнозируе- мой его рентабельности. Эта задача решается на основе применения мето- да дисконтирования. Данные вычисления имеют большое прикладное значение в проект- ном анализе для приведения денежных сумм, оцененных по состоянию на
Математическое дисконтирование по ставке сложных процентов осуществляется следующим образом:
можно определить по таблицам сложных процентов в зависимости от ставки дисконтирования и периода дисконтирования. Экономический смысл дисконтного множителя заключается в следующем: он показывает цену одной денежной единицы будущего на настоящий момент времени.
В случае предварительного начисления сложных процентов, т.е. ко- гда сложный процент (например, за кредит или за продажу какого-либо финансового документа до срока его погашения) начисляется в момент за- ключения финансового соглашения, применяется сложная учетная ставка. При этом процесс дисконтирования происходит с замедлением, т.к. каж- дый раз учетная ставка применяется не к первоначальной сумме (как при простой учетной ставке), а к сумме уже дисконтированной на предыдущем
Эффективная учетная ставка определяется по формуле:
3. Поток платежей - ряд последовательных выплат и поступлений. Выплаты представляются отрицательными величинами, а поступления - положительными. Обобщающими характеристиками потока платежей являются нара- щенная сумма и современная величина. Каждая из этих характеристик яв- ляется числом. Финансовая рента или аннуитет - поток платежей, все члены ко- торого положительные величины, а временные интервалы постоянны. Член ренты или аннуитетный платеж (А) - величина каждого от- дельного платежа. Период ренты - временной интервал между двумя соседними пла- тежами. Срок ренты (n) – время, от начала финансовой ренты до конца ее последнего периода. Процентная ставка (i) - ставка, используемая при наращении или дисконтировании платежей, Наращенная сумма аннуитета (FVA - сумма всех членов последо- вательности платежей с начисленными на них процентами к концу срока ренты. Современная величина аннуитета (PVA) - сумма всех его членов, дисконтированных (приведенных) на некоторый момент времени, совпа- дающий с началом потока платежей или предшествующий ему. Аннуитет различают по моменту выплаты платежей. Если платежи осуществляются в конце каждого периода, то такой аннуитет называют обычным или постнумерандо. Если же выплаты производятся в начале каждого периода, то аннуитет называют пренумерандо. Иногда преду- сматриваются платежи в середине каждого периода. Для аннуитета постнумерандо:
2) текущая стоимость аннуитета рассчитывается: а) если аннутетный платеж постоянен (А – const):
|
||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.250.115 (0.008 с.) |

 2. Дисконтирование денежных средств по сложным процент- ным и учетным ставкам
2. Дисконтирование денежных средств по сложным процент- ным и учетным ставкам



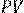
 3. Расчет аннуитетных платежей
3. Расчет аннуитетных платежей
 Процентная ставка измеряет уровень доходности отнесением аб- солютного эффекта (полученного дохода в виде суммы процентных денег, начисленных за весь срок) к исходной сумме долгового обязательства.
Процентная ставка измеряет уровень доходности отнесением аб- солютного эффекта (полученного дохода в виде суммы процентных денег, начисленных за весь срок) к исходной сумме долгового обязательства. Простые проценты начисляются по ставке i на одну и ту же посто-
Простые проценты начисляются по ставке i на одну и ту же посто- янную базу - исходную сумму долга PV, что за счет многократного при- бавления постоянной величины процентного дохода за один период при- водит к росту будущей стоимости FV за полный срок n периодов по закону арифметической прогрессии.
янную базу - исходную сумму долга PV, что за счет многократного при- бавления постоянной величины процентного дохода за один период при- водит к росту будущей стоимости FV за полный срок n периодов по закону арифметической прогрессии.

 Множитель наращения по правилу простых процентов показывает будущую стоимость одной денежной единицы, вложенной сроком на n пе- риодов при начислении в конце каждого из них процентного дохода по ставке i без капитализации (т.е. без учета или без накопления) начислен- ных ранее процентов.
Множитель наращения по правилу простых процентов показывает будущую стоимость одной денежной единицы, вложенной сроком на n пе- риодов при начислении в конце каждого из них процентного дохода по ставке i без капитализации (т.е. без учета или без накопления) начислен- ных ранее процентов.
 риоды. Наращенная сумма растет в геометрической прогрессии.
риоды. Наращенная сумма растет в геометрической прогрессии.

 Множитель наращения сложных процентов является основным финансовым коэффициентом и показывает будущую стоимость 1 денеж- ной единицы, вложенной на n периодов под сложные проценты, начисляе- мые по ставке i.
Множитель наращения сложных процентов является основным финансовым коэффициентом и показывает будущую стоимость 1 денеж- ной единицы, вложенной на n периодов под сложные проценты, начисляе- мые по ставке i.















 пользовать в финансовых соглашениях изменяющиеся во времени (пла- вающие) процентные ставки. В этом случае наращенная сумма определят- ся по формуле:
пользовать в финансовых соглашениях изменяющиеся во времени (пла- вающие) процентные ставки. В этом случае наращенная сумма определят- ся по формуле: Начисление процентов при дробном числе лет
Начисление процентов при дробном числе лет Часто срок для начисления процентов не является целым числом. В
Часто срок для начисления процентов не является целым числом. В


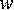




 где – целое число лет, – дробная часть года;
где – целое число лет, – дробная часть года;


 При выборе метода начисления следует иметь в виду, что множитель наращения, а следовательно и наращенная сумма, по смешанному методу оказывается несколько больше, чем по общему методу.
При выборе метода начисления следует иметь в виду, что множитель наращения, а следовательно и наращенная сумма, по смешанному методу оказывается несколько больше, чем по общему методу.


 ной единицы по номинальной годовой ставке сложных процентов i при частоте начисления m раз в год.
ной единицы по номинальной годовой ставке сложных процентов i при частоте начисления m раз в год.

 где – эффективная годовая процентная ставка.
где – эффективная годовая процентная ставка.




 различные даты, к одному требуемому моменту времени (например, со- временному).
различные даты, к одному требуемому моменту времени (например, со- временному).

 Величину называют дисконтным множителем. Его значения
Величину называют дисконтным множителем. Его значения Величину PV, полученную в процессе дисконтирования, называют современной стоимостью суммы FV. Разность FV-PV называют дискон-
Величину PV, полученную в процессе дисконтирования, называют современной стоимостью суммы FV. Разность FV-PV называют дискон- том.
том.

 При начислении процентов несколько раз в год формула дисконти- рования имеет вид:
При начислении процентов несколько раз в год формула дисконти- рования имеет вид: Таким образом, при сроке финансовой операции менее одного года дисконтирование по сложной процентной ставке даст большую величину приведенной стоимости, чем дисконтирование по простой ставке, а при сроке более одного года – наоборот. Если срок операции равен одному го- ду, то дисконтирование по обоим видам ставок приведет к одинаковым ре- зультатам.
Таким образом, при сроке финансовой операции менее одного года дисконтирование по сложной процентной ставке даст большую величину приведенной стоимости, чем дисконтирование по простой ставке, а при сроке более одного года – наоборот. Если срок операции равен одному го- ду, то дисконтирование по обоим видам ставок приведет к одинаковым ре- зультатам. шаге во времени.
шаге во времени. Дисконтирование по сложной учетной ставке осуществляется по формуле:
Дисконтирование по сложной учетной ставке осуществляется по формуле:



 где - дисконтный множитель.
где - дисконтный множитель.


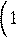




 где d – номинальная учетная ставка.
где d – номинальная учетная ставка.





 1) будущая стоимость ренты рассчитывается:
1) будущая стоимость ренты рассчитывается: а) если аннутетный платеж постоянен (А – const):
а) если аннутетный платеж постоянен (А – const):

 б) если величина каждого отдельного платежа различна:
б) если величина каждого отдельного платежа различна:

 где – номер периода ренты.
где – номер периода ренты. б) если величина каждого отдельного платежа различна:
б) если величина каждого отдельного платежа различна:




