
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Простые и сложные процентыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1.1. Виды процентных ставок
В практике финансовых расчетов суммы денег вне зависимости от их назначения или происхождения, так или иначе, но обязательно связываются конкретными моментами времени.
Необходимость учета временного фактора вытекает из сущности финансирования и кредитования и выражается в принципе неравноценности денег, относящихся к разным моментам времени. Вполне понятно, что 1000 руб., полученные через 5 лет, неравноценны этой же сумме, поступившей сегодня. Отмеченная неравноценность двух одинаковых по абсолютной величине сумм связана, прежде всего, с тем, что имеющиеся сегодня деньги теоретически могут быть инвестированы и принести доход в будущем.
Под процентными деньгами или, кратко процентами, понимают абсолютную величину дохода от предоставления денег в долг в любой его форме.
При заключении финансового или кредитного соглашения стороны договариваются о величине процентной ставки. Под процентной ставкой понимается относительная величина дохода за фиксированный отрезок времени, т.е. отношение дохода (процентов) к сумме долга за единицу времени.
Временной интервал, к которому приурочена процентная ставка, называют периодом начисления.
Проценты могут выплачиваться по мере их начисления или присоединяться к основной сумме долга. Процесс увеличения суммы денег называется наращением, или ростом этой суммы.
Процентная ставка применяется и в более широком смысле – как измеритель степени доходности (эффективность) любой финансовой операции.
Видов процентных ставок достаточно много, так как и различных видов сделок тоже множество и они могут классифицироваться по базе начислений, по принципу расчета, по размеру и т.д. Эти виды ставок будут рассмотрены в дальнейшем.
В случае если проценты за полученную ссуду определяются исходя из первоначальной суммы долга, проценты называются простыми. Каждый раз при начислении таких процентов в качестве базы берется одна и та же сумма. Начисленные за соответствующие периоды проценты выплачиваются кредитору или присоединяются к сумме долга. Для записи формулы наращения по простым процентам введем обозначения:
I – проценты за весь срок займа; Р – первоначальная сумма долга (вклада); i – ставка процента (десятичная дробь); n – число периодов начисления (срок вклада);
Рис. 1. Схема начисления процентов Начисленные проценты за один период времени равны P·i и за n периодов – P·n·i. Процесс изменения суммы долга с начисленными процентами описывается арифметической прогрессией P, P + P·i, P + 2P·i и т. д. Сумма, образовавшаяся к концу срока (обозначим ее как S) состоит из двух элементов – первоначальной суммы долга и процентов:
S = P + I = P + P·n·i = P(1 + n·i). (1)
Величину S называют наращенной суммой платежа (долга), формулу (1) – формулой наращения по простым процентам, а множитель (1 + n·i) – множителем наращения. График роста по простым процентам представлен на рис. 2.
Формула (1) связывает функциональной зависимостью четыре величины: S, P, n, i. Решив ее относительно n и i, соответственно получим:
Рассмотрим примеры решения задач.
Пример 1. Кредит в размере 100 тыс. руб. выдан на 2 года под 10% годовых. Определим подлежащую возврату сумму, если простой процент начисляется за каждый год, а долг гасится единовременным платежом.
Р = 100 т.р. Представим задачу графически: n = 2 г. S =? i = 10 %
S -?

0 1 2
Используя формулу (1) получим: S = P (1 + in) = 100 (1 + 0,1 х 2) = 120 т.р. Пример 2. Кредит в размере 100 т.р. выдан под 10% годовых. Возвращаемая сумма равна 120 тыс. руб. Определить срок вклада.
Р = 100 т.р. Представим задачу графически: i = 10 % S = 120 т.р.
n -?
0 n
Используя формулу (2) получим:
Пример 3. Кредит в 100 т.р. выдан на 2 года. Определить процентную ставку, если возвращаемая сумма составила 120 тыс. руб.
P = 100 т.р. Представим задачу графически: S = 120 т.р.
i -?
0 1 2
Используя формулу (3) получим:
Пример 4.
Кредит выдан на 2 года под 10 % годовых. Определить первоначальную сумму кредита, если возвращаемая сумма равна 120 тыс. руб.
S = 120 т.р. Представим задачу графически: i = 10 % n = 2 г.
Р -?
0 1 2
Эта задача является обратной по отношению к задаче из примера 1 (по заданной накопленной сумме найти первоначальную). Из выражения (1) следует:
S = P (1 + in) и P = S / (1 + in)
ПЕРЕМЕННЫЕ СТАВКИ
В коммерческих сделках иногда предусматриваются изменяющиеся во времени процентные ставки. В этом случае наращенная сумма определяется следующим образом:
где ik – ставка простых процентов для периода nk – продолжительность периода.
Графическая схема наращения по переменным ставкам приведена на рис. 3.
Пример 5. Соглашение промышленного предприятия с банком предусматривает выдачу кредита в 10 млн. руб. на 5 лет по базовой процентной ставке в 10%. За второй и третий годы ставка последовательно увеличивается на 2%; за четвертый год – на 5%, но относительно к базовой, а за пятый год ставка увеличивается каждый квартал на 1% по отношению к ставке за четвертый год. Определить возвращаемую сумму.
Р = 10 млн.р. Определяем величину процентных n = 5 лет ставок: im – изменяю- щаяся ставка
S -?
i1 = 10%; i2 = 10 + 2 = 12%; i3 = 12 + 2 = 14%; i4 = 10 + 5 = 15%; i5 = 15 + 1 = 16%; i6 = 16 + 1 = 17%; i7 = 17 + 1 = 18%; i8 = 18 + 1 = = 19%,
S = 10(1+1 · 0,1+1 · 0,12+1 · 0,14+1 · 0,15+1/4 · 0,16+1/4 · 0,17+1/4 · 0,18+ +1/4 · 0,19) = 10 · 1,685 = 16,85 (млн. руб.)
Реинвестирование
В практике инвестирования средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах общего заданного срока, т.е. реинвестированию полученных на каждом этапе наращения средств. Рассмотрим этот процесс подробнее (для упрощения примем, что процентные ставки и величина периода наращения не меняются). Графическая иллюстрация процесса реинвестирования приведена на рис. Обозначим первоначальную сумму депозита (вклада и т.п.) через «Р1 », процентную ставку через «i » и срок через «n ». - для первого периода наращения получим (рис.)
S1 = P1 + I1 = P1 + P1 · i = P1 · (1 + i)
- для второго периода наращения (рис.) наращенная за первый период сумма S1 принимается равной первоначальной сумме депозита за второй период, т.е. S1 = Р2, тогда наращенная сумма за второй период определяется как:
S2 = S1 + I2 = P1 · (1 + i) + S1 · i
или
S2 = P1 · (1 + i) + [ P1 · (1 + i)] · i = P1 · (1 + i)2
Эта сумма принимается за первоначальную сумму на третьем периоде наращения и т.д.
- для n -ого периода получаем аналогично
Sn = P1 · (1 + i) n (5)
Возвращаясь к принятым обозначениям это выражение можно переписать:
S = P · (1 + i * n) m, где m – количество реинвестиций.
В общем случае наращения сумма будет рассматриваться: S = P · (1+ i1 · n1) · (1+ i2 · n2) · (1+ i3 · n3) · … · P где m – количество реинвестиций
а) после первого периода наращения
б) после второго периода наращения
      
в) после n-го периода наращения
Рис. 4 Процесс реинвестирования
Рис. 5 Схема реинвестирования средств
Сумма 100 тыс. руб. вложена на один квартал с ежемесячным реинвестированием. Рассчитать накопленную сумму, если месячная ставка соответственно 10%, 15%, 20%.
Р = 100 тыс. руб. Представим задачу в графической форме: n – один квартал m – 3 i1 = 10% i2 = 15% i3 = 20%
S -?
0 1 м 2 м 3 м 1 кв
S = 100 · (1 + 1 · 0,1)(1 + 1 · 0,15)(1 + 1 · 0,2) = 100 · 1,1 · 1,15 · 1,2 = = 100 · 1,518 = 151,8 тыс. руб.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 3028; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 Время как фактор в финансовых расчетах.
Время как фактор в финансовых расчетах.
 S – наращенная (накопленная) сумма.
S – наращенная (накопленная) сумма.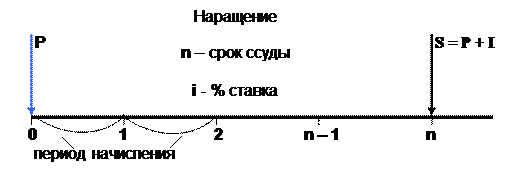

 (2)
(2)
 Дано: Решение:
Дано: Решение:








 (года)
(года) Дано: Решение:
Дано: Решение: n = 2 г.
n = 2 г.
 или 10%
или 10%

 тыс. руб.
тыс. руб. ),
),
 ;
;
 Дано: Решение:
Дано: Решение:

 наращение
наращение

 · (1+ im · nm), (6)
· (1+ im · nm), (6)



 Дано: Решение:
Дано: Решение:




