
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практикум по финансовой математикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В.Н. КРАЕВ
Практикум по финансовой математике
(учебное пособие)
Владимир 2006
Формирующийся в России рынок можно представить в виде совокупности продавцов и покупателей, дебиторов и кредиторов или совокупности контрагентов. Их взаимодействие приводит к возможности обмена товарами, услугами на рынке.
Финансовые вычисления можно представить как аппарат, который используется для приведения всего механизма взаимодействия продавцов и покупателей, контрагентов в действие. Этот аппарат является составной частью финансового менеджмента и включает математический и статистический инструментарий, методы финансового анализа.
Задачи, решение которых связано с финансовыми вычислениями, представлены на схеме:
Множественность влияющих в каждом случае факторов приводит к тому, что их совместный результат часто неочевиден (кроме, разумеется, простейших ситуаций). Необходим количественный анализ, часто выходящий за рамки элементарных расчетов. Совокупность методов расчетов, объединяемых под общим названием финансовые и коммерческие расчеты, финансовая математика, высшие финансовые вычисления, и является предметом изучения этого учебного практикума
Финансово-экономические расчеты (ФЭР) рассматривают большинство операций, в которых увеличение стоимости капитала происходит в результате предоставления его в долг и взимания процентной платы. В основе таких сделок лежат заранее оговоренные их субъектами правила получения дохода на процент, т.е. части прибыли, полученной в результате оборота фондов денежных средств в процессе производства.
ФЭР охватывают определенный круг методов вычислений, необходимость в которых возникает всякий раз, когда в условиях сделки или финансово-банковской операции оговариваются конкретные значения трех видов параметров, а именно: стоимостные характеристики (размеры платежей, долговых обязательств, кредитов и т.д.), временные данные (даты или сроки выплат, продолжительность льготных периодов или отсрочки платежей и т.п.), а также процентные ставки (они могут быть заданы в скрытой форме).
Это выражается в решении следующих задач.
1. Исчисление конечных сумм денежных средств, находящихся во вкладах, займах, ценных бумагах путем начисления процентов, а также оценка современной стоимости ожидаемых доходов. 2. Установление взаимосвязи между отдельными параметрами сделки и определение параметров сделки, исходя из заданных условий. 3. Определение эквивалентности параметров сделки для получения равной отдачи от затрат, произведенных различными способами. 4. Анализ последствий изменения условий операции. 5. Исчисление обобщающих характеристик и отдельных параметров финансовых потоков. 6. Разработка планов выполнения финансовых операций. 7. Учет ценных бумаг. 8. Расчет показателей доходности финансовых операций и финансовых инструментов.
На практике ФЭР применяются в банковском и сберегательном деле, страховании, в работе финансовых организаций, торговых фирм и инвестиционных компаний, фондовых и валютных бирж. Важное значение ФЭР имеют и для внешнеэкономических отношений.
Глава 1 знакомит читателя с сущностью и задачами финансово-экономических расчетов, оценкой финансово-экономических платежей, планированием погашения задолженности.
В главе 2 рассматриваются суть и виды инфляции, статистические методы оценки уровня инфляции в финансово-экономических расчетах.
В настоящее время известно достаточно много литературы по финансовому менеджменту, статистике финансов, основам финансовых исчислений, финансовой математике (см. список литературы).
Автор, в некоторых случаях позволил себе использовать материалы, приведенные в других изданиях, без специальных ссылок.
Виды процентных ставок
В практике финансовых расчетов суммы денег вне зависимости от их назначения или происхождения, так или иначе, но обязательно связываются конкретными моментами времени.
Необходимость учета временного фактора вытекает из сущности финансирования и кредитования и выражается в принципе неравноценности денег, относящихся к разным моментам времени. Вполне понятно, что 1000 руб., полученные через 5 лет, неравноценны этой же сумме, поступившей сегодня. Отмеченная неравноценность двух одинаковых по абсолютной величине сумм связана, прежде всего, с тем, что имеющиеся сегодня деньги теоретически могут быть инвестированы и принести доход в будущем.
Под процентными деньгами или, кратко процентами, понимают абсолютную величину дохода от предоставления денег в долг в любой его форме.
При заключении финансового или кредитного соглашения стороны договариваются о величине процентной ставки. Под процентной ставкой понимается относительная величина дохода за фиксированный отрезок времени, т.е. отношение дохода (процентов) к сумме долга за единицу времени.
Временной интервал, к которому приурочена процентная ставка, называют периодом начисления.
Проценты могут выплачиваться по мере их начисления или присоединяться к основной сумме долга. Процесс увеличения суммы денег называется наращением, или ростом этой суммы.
Процентная ставка применяется и в более широком смысле – как измеритель степени доходности (эффективность) любой финансовой операции.
Видов процентных ставок достаточно много, так как и различных видов сделок тоже множество и они могут классифицироваться по базе начислений, по принципу расчета, по размеру и т.д. Эти виды ставок будут рассмотрены в дальнейшем.
В случае если проценты за полученную ссуду определяются исходя из первоначальной суммы долга, проценты называются простыми. Каждый раз при начислении таких процентов в качестве базы берется одна и та же сумма. Начисленные за соответствующие периоды проценты выплачиваются кредитору или присоединяются к сумме долга. Для записи формулы наращения по простым процентам введем обозначения:
I – проценты за весь срок займа; Р – первоначальная сумма долга (вклада); i – ставка процента (десятичная дробь); n – число периодов начисления (срок вклада);
Рис. 1. Схема начисления процентов Начисленные проценты за один период времени равны P·i и за n периодов – P·n·i. Процесс изменения суммы долга с начисленными процентами описывается арифметической прогрессией P, P + P·i, P + 2P·i и т. д. Сумма, образовавшаяся к концу срока (обозначим ее как S) состоит из двух элементов – первоначальной суммы долга и процентов:
S = P + I = P + P·n·i = P(1 + n·i). (1)
Величину S называют наращенной суммой платежа (долга), формулу (1) – формулой наращения по простым процентам, а множитель (1 + n·i) – множителем наращения. График роста по простым процентам представлен на рис. 2.
Формула (1) связывает функциональной зависимостью четыре величины: S, P, n, i. Решив ее относительно n и i, соответственно получим:
Рассмотрим примеры решения задач.
Пример 1. Кредит в размере 100 тыс. руб. выдан на 2 года под 10% годовых. Определим подлежащую возврату сумму, если простой процент начисляется за каждый год, а долг гасится единовременным платежом.
Р = 100 т.р. Представим задачу графически: n = 2 г. S =? i = 10 %
S -?

0 1 2
Используя формулу (1) получим: S = P (1 + in) = 100 (1 + 0,1 х 2) = 120 т.р. Пример 2. Кредит в размере 100 т.р. выдан под 10% годовых. Возвращаемая сумма равна 120 тыс. руб. Определить срок вклада.
Р = 100 т.р. Представим задачу графически: i = 10 % S = 120 т.р.
n -?
0 n
Используя формулу (2) получим:
Пример 3. Кредит в 100 т.р. выдан на 2 года. Определить процентную ставку, если возвращаемая сумма составила 120 тыс. руб.
P = 100 т.р. Представим задачу графически: S = 120 т.р.
i -?
0 1 2
Используя формулу (3) получим:
Пример 4.
Кредит выдан на 2 года под 10 % годовых. Определить первоначальную сумму кредита, если возвращаемая сумма равна 120 тыс. руб.
S = 120 т.р. Представим задачу графически: i = 10 % n = 2 г.
Р -?
0 1 2
Эта задача является обратной по отношению к задаче из примера 1 (по заданной накопленной сумме найти первоначальную). Из выражения (1) следует:
S = P (1 + in) и P = S / (1 + in)
ПЕРЕМЕННЫЕ СТАВКИ
В коммерческих сделках иногда предусматриваются изменяющиеся во времени процентные ставки. В этом случае наращенная сумма определяется следующим образом:
где ik – ставка простых процентов для периода nk – продолжительность периода.
Графическая схема наращения по переменным ставкам приведена на рис. 3.
Пример 5. Соглашение промышленного предприятия с банком предусматривает выдачу кредита в 10 млн. руб. на 5 лет по базовой процентной ставке в 10%. За второй и третий годы ставка последовательно увеличивается на 2%; за четвертый год – на 5%, но относительно к базовой, а за пятый год ставка увеличивается каждый квартал на 1% по отношению к ставке за четвертый год. Определить возвращаемую сумму.
Р = 10 млн.р. Определяем величину процентных n = 5 лет ставок: im – изменяю- щаяся ставка
S -?
i1 = 10%; i2 = 10 + 2 = 12%; i3 = 12 + 2 = 14%; i4 = 10 + 5 = 15%; i5 = 15 + 1 = 16%; i6 = 16 + 1 = 17%; i7 = 17 + 1 = 18%; i8 = 18 + 1 = = 19%,
S = 10(1+1 · 0,1+1 · 0,12+1 · 0,14+1 · 0,15+1/4 · 0,16+1/4 · 0,17+1/4 · 0,18+ +1/4 · 0,19) = 10 · 1,685 = 16,85 (млн. руб.)
Реинвестирование
В практике инвестирования средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах общего заданного срока, т.е. реинвестированию полученных на каждом этапе наращения средств. Рассмотрим этот процесс подробнее (для упрощения примем, что процентные ставки и величина периода наращения не меняются). Графическая иллюстрация процесса реинвестирования приведена на рис. Обозначим первоначальную сумму депозита (вклада и т.п.) через «Р1 », процентную ставку через «i » и срок через «n ». - для первого периода наращения получим (рис.)
S1 = P1 + I1 = P1 + P1 · i = P1 · (1 + i)
- для второго периода наращения (рис.) наращенная за первый период сумма S1 принимается равной первоначальной сумме депозита за второй период, т.е. S1 = Р2, тогда наращенная сумма за второй период определяется как:
S2 = S1 + I2 = P1 · (1 + i) + S1 · i
или
S2 = P1 · (1 + i) + [ P1 · (1 + i)] · i = P1 · (1 + i)2
Эта сумма принимается за первоначальную сумму на третьем периоде наращения и т.д.
- для n -ого периода получаем аналогично
Sn = P1 · (1 + i) n (5)
Возвращаясь к принятым обозначениям это выражение можно переписать:
S = P · (1 + i * n) m, где m – количество реинвестиций.
В общем случае наращения сумма будет рассматриваться: S = P · (1+ i1 · n1) · (1+ i2 · n2) · (1+ i3 · n3) · … · P где m – количество реинвестиций
а) после первого периода наращения
б) после второго периода наращения
      
в) после n-го периода наращения
Рис. 4 Процесс реинвестирования
Рис. 5 Схема реинвестирования средств
Сумма 100 тыс. руб. вложена на один квартал с ежемесячным реинвестированием. Рассчитать накопленную сумму, если месячная ставка соответственно 10%, 15%, 20%.
Р = 100 тыс. руб. Представим задачу в графической форме: n – один квартал m – 3 i1 = 10% i2 = 15% i3 = 20%
S -?
0 1 м 2 м 3 м 1 кв
S = 100 · (1 + 1 · 0,1)(1 + 1 · 0,15)(1 + 1 · 0,2) = 100 · 1,1 · 1,15 · 1,2 = = 100 · 1,518 = 151,8 тыс. руб.
Пример 7.
Акционерное общество (АО) для погашения задолженности по счетам поставщиков считает возможным взять краткосрочный кредит под 40% годовых. Год не високосный. Ссуда 100 млн. руб. планируется с 20 января по 5 марта включительно. Определим возможные варианты возврата долга. Точное число дней ссуды определяем по таблице 1. Оно равно: 64 – 20 = 44 дн. Приближенное число дней ссуды равно: 11 дн. января (т.к. число дней принимается равным 30) + 30 дн. (один полный месяц) + 5 дн. марта – 1 = 45 дн. Возможные варианты возврата долга: 1) по точным процентам с точным числом дней ссуды: S = 100 (1 + 44/365 · 0,4) = 100 (1 + 0,1205479 · 0,4) = 104,82191 млн. руб. 2) по обыкновенным процентам с точным числом дней ссуды: S = 100 (1 + 44/360 · 0,4) = 100 (1 + 0,1222222 · 0,4) = 104,88889 млн. руб. 3) по обыкновенным процентам с приближенным числом дней ссуды: S = 100 (1 + 45/360 · 0,4) = 100 (1 + 0,125 · 0,4) = 105,0 млн. руб. Вариационный размах наращенных сумм по вариантам ссуды значителен и составляет 180 тыс. руб. Такая разница в вариантах сделки весьма существенна, особенно если предположить, что речь идет об инвалюте.
ОСНОВНЫЕ ПОНЯТИЯ Кредит в условиях рынка выступает в различных формах. Основными являются коммерческий и банковский кредиты. Коммерческий кредит связан с продажей товаров и отсрочкой платежа на определенное время. Таким образом, объектом этого кредита являются средства в товарной форме. Кредитным документом является коммерческий вексель. Он представляет собой письменное долговое обязательство, составленное по установленной форме. Вексель предоставляет векселедержателю бесспорное право по истечении срока векселя требовать от должника (векселедателя) указанную в векселе сумму. Векселя бывают простые и переводные. Простой вексель (соло-вексель) – это обязательство покупателя товара уплатить в указанный срок определенную сумму продавцу. Вексель выписывается покупателем и передается продавцу товара. Переводной вексель (тратта) представляет собой письменный приказ продавца (трассанта) покупателю (трассату) об уплате обозначенной в векселе суммы в указанный срок третьему лицу (ремитенту). Передаточная надпись на обратной стороне векселя называется индоссамент. С помощью индоссамента вексель может передаваться многократно, по существу являясь денежным документом. Банковский кредит состоит в предоставлении банками предпринимателям и другим заемщикам денежных кредитов или денежных ссуд. Здесь, в отличие от коммерческого кредита, объектом являются денежные средства. Использование в обращении банковских векселей расширяют масштабы вексельного оборота и делают его более обеспеченным вследствие гарантий, выдаваемых банками. Вексель используется как платежное средство. В случае необходимости получения денег по векселю ранее указанного срока векселедержатель может продать его банку по более низкой цене, т. е. ниже суммы, указанной на векселе. Сумма, указанная на векселе, является его номинальной стоимостью. Такая сделка носит название учета векселя или дисконтирования. По существу, дисконтирование – это задача, обратная наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. Такая ситуация может возникнуть, например, при разработке условий контракта. Расчет P по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды. В этих случаях, говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называется учетом, а удержанные проценты (или разница между номинальной стоимостью долгового обязательства и суммой, полученной векселедержателем в результате учета векселя) – дисконтом.
Величину P, найденную с помощью дисконтирования, называют современной величиной суммы S, а иногда, в зависимости от контекста – современной (текущей, капитализированной) стоимостью. Современная величина в сумме денег является одним из важнейших понятий в количественном анализе финансовых операций. В большинстве случаев именно с помощью дисконтирования, а не наращения учитывается такой фактор, как время. Логика финансовых операций наращения и дисконтирования приведена на рис. 6. НАСТОЯЩЕЕ БУДУЩЕЕ
Рис. 6. Логика финансовых операций
Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды. Задача в этом случае формулируется так: какую первоначальную сумму ссуды надо выдать в долг, чтобы получить в конце срока сумму S при условии, что на долг начисляются проценты по ставке i? Решив уравнение (1) относительно P, находим:
Установленная таким путем величина P является современной величиной суммы S, которая будет выплачена через n лет. Выражение 1/(1 + n∙i) называется дисконтным множителем, который показывает современную стоимость одной денежной единицы. Разность (S – P) можно рассматривать не только как проценты, начисляемые на P, но и как дисконт суммы S. Обозначим последний через D. Дисконт, как скидка с конечной суммы долга необязательно определяется через процентную ставку, он может быть установлен по соглашению сторон и в виде абсолютной величины для всего срока. Рассмотрим примеры.
Пример 8. Через год владелец векселя, выданного коммерческим банком, должен получить по нему 220 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если годовая ставка составляет 12%?
S = 220 т.р. Представим задачу графически i = 12% n = 1 год
Р -?
дисконтирование 0 1 2
Пример 9. Ссуда должна быть погашена через год в сумме 200 тыс. руб. Кредитор попросил погасить ссуду через 270 дней после выдачи под 10% годовых. Какую сумму получит кредитор? К = 365 дн.
S = 200 тыс. руб. Изобразим задачу графически: I = 10% n = 1г.
Р -?
дисконтирование

Находим количество дней, оставшихся до погашения ссуды: n0 = n – n1 = 365 – 270 = 95 (дн.) Используя выражение (12) находим:
Рис. 7 Пример 10.
Владелец векселя номиналом 100 тыс. руб. и периодом обращения 105 дн., за 15 дн. до наступления срока платежа учитывает его в банке по учетной ставке 20%. Определить сумму, полученную владельцем векселя.
S = 100 тыс. руб. Изобразим задачу графически: Пер. обращение – 105 дн. n = 15 дн. d = 20%
Р -? Р -? S = 100 n = 15 дн.
d = 20%
Используя выражение (13а) получим:
В отдельных случаях может возникнуть ситуация, когда совмещается начисление процентов по ставке наращения i и дисконтирование по учетной ставке d. В этом случае, полученная при учете сумма определиться как:
S` где P(S) – номинальная сумма; n – общий срок платежного обязательства; n` - срок от момента учета до даты погашения платежа; Р` - сумма, полученная при учете обязательства. Пример 11.
Долговое обязательство, предусматривающее уплату 400 тыс. руб. с начисленными на них 12% годовых, подлежит погашению через 90 дн. Владелец обязательства (кредитор) учел его в банке за 15 дн. до наступления срока по учетной ставке 13,5%. Полученная сумма после учета составила:
S = 400 тыс. руб. В этой задаче номинальная стоимость n = 90 дн. (возвращаемая сумма) принимается за n` = 15 дн. первоначальную: S = P (см. график). d = 13,5% i = 12%
P(S) =400 т.р. S`
i = 12%; n = 90 дн.
d = 13,5%; n` = 15дн.
дисконтирование P` -? 1. Вначале определяем наращенную сумму обязательства S`, принимая его номинальную стоимость за первоначальную сумму:
2. Находим полученную после учета сумму:
3. Используя выражение (14) получаем ту же сумму:
Необходимость использования простой учетной ставки для расчета наращенной суммы возникает в случае определения номинальной стоимости векселя при выдаче ссуды. В этом случае сумма долга, проставленная в векселе, будет равна
Величина 1/(1- n ∙ d) в этом случае является множителем наращения при использовании простой учетной ставки.
Пример 12.
Предприниматель обратился в банк за ссудой в размере 200 тыс. руб. на срок 55 дней. Банк согласен выдать указанную сумму при условии начисления процентов по простой учетной ставке, равной 20%. Найти возвращаемую сумму. Дано: Решение:
n = 55 дн. по простой учетной ставке.
S -?
Р = 200 S -? наращение

d = 20; n = 55 дн.
Используя выражение (15) получим:
Если бы сумма выдавалась под простую процентную ставку ( i), то наращенная сумма была бы равна |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 711; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |


 Введение
Введение
 S – наращенная (накопленная) сумма.
S – наращенная (накопленная) сумма.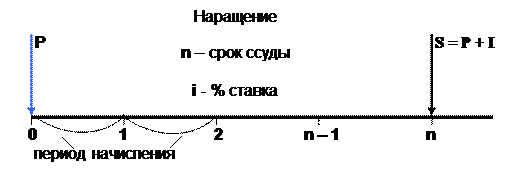

 (2)
(2)
 Дано: Решение:
Дано: Решение:








 (года)
(года) Дано: Решение:
Дано: Решение: n = 2 г.
n = 2 г.
 или 10%
или 10%

 тыс. руб.
тыс. руб.
 ),
),
 ;
;
 Дано: Решение:
Дано: Решение:

 наращение
наращение

 · (1+ im · nm), (6)
· (1+ im · nm), (6)



 Дано: Решение:
Дано: Решение:

 Термин «дисконтирование» употребляется и в более широком смысле – как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени. Такой прием часто называют приведением стоимостного показателя к некоторому, обычно начальному моменту времени.
Термин «дисконтирование» употребляется и в более широком смысле – как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени. Такой прием часто называют приведением стоимостного показателя к некоторому, обычно начальному моменту времени. МАТЕМАТИЧЕСКОЕ ДИСКОНТИРОВАНИЕ
МАТЕМАТИЧЕСКОЕ ДИСКОНТИРОВАНИЕ (12)
(12) Дано: Решение:
Дано: Решение:

 тыс. руб.
тыс. руб. n1 = 270 дн.
n1 = 270 дн.

 (тыс. руб.)
(тыс. руб.)



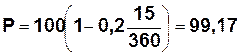 (тыс. руб.)
(тыс. руб.) P` = P ∙ (1 + n ∙ i) ∙ (1 – n` ∙ d) (14)
P` = P ∙ (1 + n ∙ i) ∙ (1 – n` ∙ d) (14) Дано: Решение:
Дано: Решение: Р` -?
Р` -?


 (тыс. руб.)
(тыс. руб.) (тыс. руб.)
(тыс. руб.) (тыс. руб.)
(тыс. руб.) (15)
(15)
 Р = 200 тыс. руб. В этой задаче наращение производится
Р = 200 тыс. руб. В этой задаче наращение производится d = 20%
d = 20%
 тыс. руб.
тыс. руб.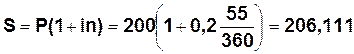 тыс.руб., т.е. наращение по учетной ставке идет быстрее и она менее выгодна должнику 206,111 < 206,304 т.е. возвращаемая сумма в первом случае будет б
тыс.руб., т.е. наращение по учетной ставке идет быстрее и она менее выгодна должнику 206,111 < 206,304 т.е. возвращаемая сумма в первом случае будет б 


