Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ставка наращения и учетная ставка.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Эквивалентные ставки Как видно из предыдущих разделов, и ставка наращения, и учетная ставка применяются для решения сходных задач. Однако для ставки наращения прямой задачей является определение наращенной суммы, обратной – дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная – в наращении.
Ставки Прямая задача Обратная задача i S = P (1 + n∙i) P = S /(1 + n∙i) d P = S (1 – n∙d) S = P /(1 – n∙d)
Однако дисконтирование по процентной ставке и учетной ставке приводит к различным результатам, даже если i = d. То есть при банковском дисконтировании владелец векселя получит меньшую сумму, чем при использовании математического дисконтирования. Это является следствием того, что учетная ставка отражает фактор времени более жестко. Так, из формулы (13) следует, что при n >1/ d величина дисконтного множителя и, следовательно, суммы P станет отрицательной. Иначе говоря, при относительно большом сроке векселя учет может привести к нулевой или даже отрицательной сумме P, что лишено смысла. Например, при d = 20% уже пятилетний срок достаточен для того, чтобы владелец векселя ничего не получил при его учете. Влияние фактора времени усиливается при увеличении величины ставки. Так, при d = 100% отрицательный результат проявится уже при n >1. Такая ситуация не возникает при математическом дисконтировании: при любом сроке современная величина платежа здесь больше нуля. Для иллюстрации сказанного на рис. 8 и в табл. 2 приведены дисконтные множители (ДМ), когда i = d = 20%.
Рис. 8. Величина дисконтного Рис. 9. Величина множителя множителя наращения
Таблица 2 Дисконтные множители, i = d = 20%
Таблица 3 Множители наращения, i = d = 20%
Выбор конкретного вида ставок заметно влияет на финансовые итоги операций. Однако возможен такой подбор величины ставок, при котором результаты будут равноценными. Для одних и тех же значений i и d из формул (12) и (13) можно записать:
d = i /(1 + n∙i)
В дальнейшем различные ставки, которые дают одно и то же значение наращенной суммы (при фиксированном сроке), будем называть эквивалентными ставками. Полученные эквивалентные ставки могут быть применены при сравнении доходности сделок, в которых применяются различные виды ставок. Легко заметить, что с уменьшением n различия между эквивалентными ставками i и d становятся менее ощутимыми (табл. 4). Таблица 4 Эквивалентные ставки
Пример 17.
Коммерческий дисконтный вексель со сроком погашения 30.06 учитывается за 18 дней до срока по учетной ставке – 10%. Определить эквивалентную ставку простых процентов.
d = 10% t = 18 дн. к = 360 дн.
i -? Р d = 10% S
n = 18 дн.; i -?
Используя выражение (21) получим:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 764; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.221 (0.006 с.) |

 Сравнивая формулы (1) и (13) легко понять, что учетная ставка дает более быстрый рост суммы задолженности, чем такой же величины ставка наращения. Множители наращения (МН) для двух видов ставок при условии, что i = d = 20%, показаны на рис. 9 и в табл. 3.
Сравнивая формулы (1) и (13) легко понять, что учетная ставка дает более быстрый рост суммы задолженности, чем такой же величины ставка наращения. Множители наращения (МН) для двух видов ставок при условии, что i = d = 20%, показаны на рис. 9 и в табл. 3.
 ДM MH
ДM MH , (20)
, (20) откуда i = d /(1 – n∙d)
откуда i = d /(1 – n∙d) 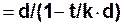 , (21)
, (21)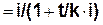 . (22)
. (22) Дано: Решение:
Дано: Решение: