
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции наращения и дисконтированияСодержание книги Поиск на нашем сайте
Логику алгоритма составляет следующая схема простейшей финансовой сделки: кредитор однократно предоставляет в долг сумму
Итак, возвращаемая через время
Как охарактеризовать эффективность (результативность) этой сделки? Введем для этого два показателя: а) абсолютный показатель: б) относительный показатель, в качестве которого рассмотрим относительный прирост: 1) за базу сравнения современная (текущая) стоимость:
которая называется процентной ставкой, процентом, ростом, нормой прибыли, доходность; 2) за базу сравнения взята будущая (наращенная) стоимость:
которая называется учетной ставкой, дисконтом.
На рис. 1 схематично показаны процесс простой финансовой сделки.
Следует иметь в виду, что данные соотношения справедливы для конкретной сделки.
В оценке финансовой сделки присутствуют значения денежных сумм, относящиеся к различным моментам времени. Процесс изменения денежных сумм, рассматриваемый с точки зрения настоящего момента времени, называют процессом наращения. Процесс изменения денежных сумм, рассматриваемый с точки зрения будущего момента времени, называют процессом дисконтирования (скидки). На рис. 2 это показано схематично.
Замечание. 1. В прогнозных расчетах обычно используют процентную ставку 2. При нестабильности экономики процентная ставка значительно изменяется, поэтому для прогнозов используют методы принятия решений, основанные на неформальных процедурах. 3. Другими показателями эффективности сделки могут быть: Ø дисконт – фактор: Ø индекс роста суммы 4. Различают: Ø декурсивный (последующий) процент, когда его начисление производят по процентной ставке Ø антисипативный (предварительный) процент, когда начисление производят по учетной ставке 5. Параметры сделки
6. Результат взаимодействия сторон финансовой сделки выражается в структуре ставки:
где
7. Использование различных схем наращения или дисконтирования обозначается общим понятием «приведение к дате».
Простые проценты Годовая процентная ставка и годовая учетная ставка
За единицу измерения промежутка времени выбирается интервал времени в 1 год и выбираются годовые ставки
тде
Замечание. 1. Относительно продолжительности финансовой операции договорились, что день выдачи и день погашения ссуды считать за один день. 2. По продолжительности года проценты подразделяются: Ø на точные проценты, когда Ø обыкновенные проценты: 3. В результате используют три схемы расчёта отношения а) схема 360/360, называемая обыкновенными процентами (Германия, Дания, Швеция); в) схема 365/360, применяемая, например, в Бельгии, Франции; г) схема 365/365, называемая точными процентами (Англия, США).
|
|||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.174.253 (0.008 с.) |

 (present value, современная стоимость) с условием, что через время
(present value, современная стоимость) с условием, что через время  будет возвращена большая сумма
будет возвращена большая сумма  (future value), где
(future value), где (interest, доход).
(interest, доход). .
.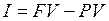 ; но он не годится для сопоставления сделок;
; но он не годится для сопоставления сделок;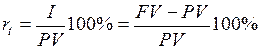 ,
, ,
,
 Связь между процентной ставкой
Связь между процентной ставкой  и учетной ставкой
и учетной ставкой  :
: .
.
 ,
, .
.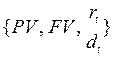 связаны одним уравнением. Поэтому для их оценки необходимо знать два, а третий находят из уравнения.
связаны одним уравнением. Поэтому для их оценки необходимо знать два, а третий находят из уравнения. ,
, норма процента (компенсация кредитору за отказ использовать в других целях предоставляемую сумму в течение времени
норма процента (компенсация кредитору за отказ использовать в других целях предоставляемую сумму в течение времени  фактор риска (за неопределённость в получении процентов или всей суммы по истечение срока кредита);
фактор риска (за неопределённость в получении процентов или всей суммы по истечение срока кредита); инфляционная добавка (за уменьшение покупательной способности денег за время
инфляционная добавка (за уменьшение покупательной способности денег за время  компенсация, зависящая от срока
компенсация, зависящая от срока  (нижний индекс «1» не указывается). Далее предполагают, что
(нижний индекс «1» не указывается). Далее предполагают, что
 ,
, обозначение интервала времени в 1 год, измеренного в единицах времени: год = 12 месяцев = 2 полугодия = 4 квартала = 365 (366) дней. Интервал
обозначение интервала времени в 1 год, измеренного в единицах времени: год = 12 месяцев = 2 полугодия = 4 квартала = 365 (366) дней. Интервал  безразмерное и обычно выражает число лет и может быть целым, дробным или десятичным числом. В формулах годовые ставки рассматриваются как безразмерные коэффициенты. Например, если задана годовая ставка
безразмерное и обычно выражает число лет и может быть целым, дробным или десятичным числом. В формулах годовые ставки рассматриваются как безразмерные коэффициенты. Например, если задана годовая ставка  , то в формулах она будет встречаться как
, то в формулах она будет встречаться как  .
.
 ;
; .
. :
:


