
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм схемы простых процентовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
А) алгоритм с применение годовой процентной ставки В формулу
подставим
получим
Решив последнее равенство относительно
Разрешив формулу (1) относительно
Проценты равны
Замечание. Формулу (3) можно записать в виде
где
В) алгоритм с применением годовой учетной ставки
В формулу
подставим
и получим равенство
которое разрешим относительно
Разрешив равенство (4) относительно
В формулах (4) и (5) должно быть
т. е. учётная ставка более жёстко отражает фактор времени. Замечание. 1. Условимся в дальнейших формулах вместо
2. Расчеты по формуле (5) называют банковским дисконтированием (банковским учётом), поскольку они применяются банками при операции учёта векселей. Вексель – письменное безусловное обязательство векселедателя (заёмщика) уплатить в установленный срок определённую сумму предъявителю векселя или лицу, указанному в векселе.
Расчёт процентов при изменяющейся сумме вклада на счёте
На рис. 3 показан график изменения суммы вклада на счёте, где Если проценты за период
Суммируя по всем периодам, получаем общую сумму процентов по вкладу:
Полученный результат можно очевидным образом обобщить на произвольное число периодов срока хранения вклада на счёте. Замечание. Рассмотренный пример показывает, что в схеме простых процентов начисление процентов производится по периодам, в течение которых исходная сумма денежных средств не изменяется.
Наращение по схеме простых процентов при переменной ставке Наличие инфляции заставляет варьировать процентную ставку
где
Если общий срок предоставления ссуды равен
наращенная сумма
Наращение с капитализацией (реинвестированием) процентов
Пусть срок ссуды разбит на В первом периоде наращенная сумма процентов составила
и эти проценты были присоединены к основной сумме
Это в конце второго периода даст сумму процентов
а наращенная сумма за два периода будет равна
Обобщая на все
Важным является частный случай, когда все интервалы времени
Замечание. Формула (13) приводит нас к схеме сложных процентов.
Факторный учёт векселя
Рассмотрим диаграмму, которая наглядно показывает составляющие схему учёта банком векселя (рис. 4) Заёмщик решил взять кредит на сумму
По истечении некоторого времени
где
Однако, банк, оказывая услугу по учёту векселя, желает получить комиссионные
При этом
|
|||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.101 (0.011 с.) |

 .
.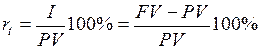


 .
. , получим формулу наращения по схеме простых процентов с применением годовой ставки процентов:
, получим формулу наращения по схеме простых процентов с применением годовой ставки процентов: . (1)
. (1) , получим формулу математического дисконтирования по схеме простых процентов:
, получим формулу математического дисконтирования по схеме простых процентов: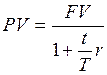 . (2)
. (2) . (3)
. (3) ,
, дивизор,
дивизор,  процентное число.
процентное число. .
.


 ,
, . (4)
. (4) . (5)
. (5)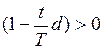 , что накладывает ограничение на период кредитования
, что накладывает ограничение на период кредитования  при заданном значении учетной ставки
при заданном значении учетной ставки  . (6)
. (6) писать просто
писать просто  . Например, формулу (1) теперь запишем в виде:
. Например, формулу (1) теперь запишем в виде: .
. сумма вклада, хранящаяся неизменной в течение интервала времени
сумма вклада, хранящаяся неизменной в течение интервала времени  .
. 
 . (7)
. (7) . (8)
. (8) ,
, база (норма) процента,
база (норма) процента,  маржа (margin) равная примерно
маржа (margin) равная примерно  . Пусть
. Пусть  процентная ставка на интервале времени
процентная ставка на интервале времени  . Тогда наращенная сумма равна
. Тогда наращенная сумма равна . (9)
. (9) , то взвешенная средняя процентная ставка
, то взвешенная средняя процентная ставка , (10)
, (10) . (11)
. (11)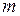 периодов длительностью
периодов длительностью  .
.
 . Таким образом, в следующем периоде наращение производится на сумму
. Таким образом, в следующем периоде наращение производится на сумму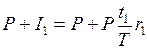
 .
. ,
,
 .
. . (12)
. (12) , и равны процентные ставки:
, и равны процентные ставки:  . Тогда формула (12) принимает вид:
. Тогда формула (12) принимает вид: . (13)
. (13) на срок
на срок  к моменту погашению. Эта сумма была вычислена по схеме простых процентов:
к моменту погашению. Эта сумма была вычислена по схеме простых процентов: .
. владелец векселя принял решение учесть в банке (продать банку и получить наличными или положить на счёт для дальнейшего использования). Время до момента погашения векселя равно
владелец векселя принял решение учесть в банке (продать банку и получить наличными или положить на счёт для дальнейшего использования). Время до момента погашения векселя равно  выбирается им в соответствии с выполнением неравенства (6):
выбирается им в соответствии с выполнением неравенства (6): ,
,
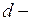 учётная ставка, которую предложил банк владельцу векселя. На момент учёта векселя наращенная стоимость
учётная ставка, которую предложил банк владельцу векселя. На момент учёта векселя наращенная стоимость .
. и проценты
и проценты  , которые в сумме составляют дисконт (скидку)
, которые в сумме составляют дисконт (скидку)  с суммы
с суммы  .
. . Комиссионные за услугу составят
. Комиссионные за услугу составят .
.


