
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение срока ссуды и величины ставкиСодержание книги
Поиск на нашем сайте
При практических финансовых вычислениях часто решаются простые задачи: а) даны
б) даны
Вычисление средних значений Предоставляя многочисленные кредиты с различными параметрами, кредитор желает знать средние значения ставок, периодов предоставления кредита. Эти параметры являются статистическими значениями, вычисляемыми по совокупности конкретных финансовых сделок. Пусть Для вычисления средних значений
или
Поскольку
из которого следует
Если ввести взвешенную среднюю арифметическую процентную ставку
то среднее время предоставления ссуды составит
Формула (20) определяет среднее время предоставления ссуды в виде взвешенной средней арифметической частных периодов. Если ввести взвешенную среднюю арифметическую процентную ставку
то среде время предоставления ссуды составит
Пусть теперь
Пусть клиент хочет получить ссуду
или при условии
Если положить, что среднее значение учетной ставки
то среднее значение срока предоставления ссуды
Если теперь положить
то
Сравнивая формулы (17 – 22) с соответствующими формулами (23 – 28), замечаем, что они являются симметричными, т.е. получаются заменой Р на F и r на d.
Замена платежей и их консолидация
При замене параметров платежей или их консолидации (несколько платежей объединяются в один) формируется финансовый эквивалент, включающий суммы, приведенные к одному и тому же моменту времени. Он имеет форму:
Поскольку финансовый эквивалент представляет собой одно равенство с несколькими параметрами, в частности, следует определить либо новую сумму платежей
при применении процентной ставки;
при применении учётной ставки. Если в новом соглашении положить
при применении процентной ставки;
при применении учётной ставки. Для случая более простой ситуации, когда параметры одного платежа заменяются новыми значениями, можно рассуждать так: а) при отдалении срока платежа наращиваются проценты:
при применении процентной ставки; б) при сокращении срока платежа, т. е.
Сложные проценты
Наращение сложных процентов
Для поощрения долгосрочных вкладов клиентов применяют процедуру капитализации процентов, т. е. присоединение начисленных процентов к базе и в дальнейшем начисление процентов на эту сумму. Такая схема процентов называется схемой сложных процентов. Наиболее простой вид алгоритма наращения по схеме сложных процентов получим, если в формуле (13) положим
В общем случае в формуле (35) число Поучаемые проценты
Если
Замечание. Отвечая на вопрос «Чему равно Ø по схеме простых процентов Ø по схеме сложных процентов
Смешанная схема процентов
Сравнение процессов наращения по схеме простых процентов со схемой сложных процентов показывает, что на временном интервале до 1 года наращенная сумма по схеме простых процентов оказывается больше. Отсюда вывод: кредитор применяет схему сложных процентов на интервалах более 1 года, а простую – на интервалах до 1 года. Если
Тогда исчисление наращенной суммы по формуле
называют смешанной схемойсложных процентов.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.006 с.) |

 ; определить период предоставления ссуды
; определить период предоставления ссуды  :
: ; (14)
; (14) ; определить ставки:
; определить ставки: . (15)
. (15) ,
,  , совокупность долгов с декурсивными процентами, а
, совокупность долгов с декурсивными процентами, а  среднее время предоставления совокупной ссуды
среднее время предоставления совокупной ссуды  , средняя процентная ставка.
, средняя процентная ставка. требуется учесть интересы кредиторов и заёмщиков. Для этих целей составляются финансовые соотношения, имеющие смысл уравнений и называемые финансовыми эквивалентами. В данном случае составляется финансовый эквивалент:
требуется учесть интересы кредиторов и заёмщиков. Для этих целей составляются финансовые соотношения, имеющие смысл уравнений и называемые финансовыми эквивалентами. В данном случае составляется финансовый эквивалент: (16)
(16)
 .
.
 , (17)
, (17)
 . (18)
. (18)
 , (19)
, (19) . (20)
. (20) , (21)
, (21) . (22)
. (22) ,
,  .
. на срок
на срок  под среднюю учетную ставку
под среднюю учетную ставку  . В этом случае финансовый эквивалент
. В этом случае финансовый эквивалент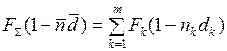 (23)
(23) получим, что
получим, что
 . (24)
. (24)
 , (25)
, (25) . (26)
. (26) , (27)
, (27) . (28)
. (28)
 , либо новый срок
, либо новый срок  платежа, то это равенство дисконтированных сумм:
платежа, то это равенство дисконтированных сумм:
 (29)
(29) (30)
(30) (31)
(31) (32)
(32) ,
,  , (33)
, (33) , надо сумму
, надо сумму  математически дисконтировать на срок
математически дисконтировать на срок  :
: . (34)
. (34) :
: ,
,  . (35)
. (35) положительное вещественное число (целое или дробное). Так, если
положительное вещественное число (целое или дробное). Так, если  наращенная сумма за
наращенная сумма за 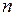 годовых периодов при начальной сумме
годовых периодов при начальной сумме  ссуды при процентной ставке
ссуды при процентной ставке  . Множитель
. Множитель  называется множителем наращения.
называется множителем наращения. . (36)
. (36)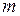 периодов начисления с капитализацией процентов произвольны, но исчисляется каждый целым числом лет
периодов начисления с капитализацией процентов произвольны, но исчисляется каждый целым числом лет  и годовая ставка процентов
и годовая ставка процентов  переменная, то наращенная сумма
переменная, то наращенная сумма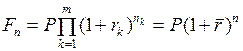 ,
,  , (37)
, (37) .
. ?», получим:
?», получим: ;
; .
. .
. (38)
(38)


