
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра математических и естественных наукСодержание книги
Поиск на нашем сайте
Кафедра математических и естественных наук
Клюжев Н.А., Ганго С.Е.
Основы финансовых вычислений КОНСПЕКТ ЛЕКЦИЙ Для всех специальностей Псков
Оглавление
ОСНОВЫ ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ (конспект лекций)
Государственные образовательные стандарты для специалистов в области экономики в обязательном порядке содержат тему, посвященную основам финансовых вычислений. В данном конспекте этой темы изложены основные расчетные схемы: простые и сложные проценты, замену платежей и их сроков, денежные потоки.
Время как фактор стоимости
Переход в России к рыночной экономике позволил: Ø упразднить ряд ограничений, например, на нормирование на предприятии оборотных средств, что служило основным регулятором величины его финансовых ресурсов; Ø изменить порядок исчисления финансовых результатов деятельности предприятия и распределения прибыли, что ведет к появлению свободных денежных средств; Ø производить переоценку роли финансовых роли финансовых ресурсов, что равносильно требованию грамотно ими управлять по видам, начислению, по времени и т.п.; Ø использовать принципиально новые виды финансовых ресурсов, в управлении которыми решающее значение имеет временной фактор; Ø применять новые варианты инвестирования капитала, в частности. в коммерческие банки, участвовать в рисковых предприятиях, приобретать ценные бумаги, недвижимость и т. п.
Итак, деньги приобрели временную ценность и причины этому в существовании временного обесценивания денежной наличности, возможность обращения денежных средств, инфляция, случайность величины доходов, оказание дополнительных услуг и т. п. Возникла проблема: как с позиций текущего момента определить истинную цену будущих доходов? Решение подобного рода проблем найдено в применении принципа неравноценности денег, относящихся к различным моментам времени, т. е. неправомерно суммировать денежные величины, относящиеся к различным моментам времени.
Простые проценты Расчёт процентов при изменяющейся сумме вклада на счёте
На рис. 3 показан график изменения суммы вклада на счёте, где
Если проценты за период
Суммируя по всем периодам, получаем общую сумму процентов по вкладу:
Полученный результат можно очевидным образом обобщить на произвольное число периодов срока хранения вклада на счёте. Замечание. Рассмотренный пример показывает, что в схеме простых процентов начисление процентов производится по периодам, в течение которых исходная сумма денежных средств не изменяется.
Факторный учёт векселя
Рассмотрим диаграмму, которая наглядно показывает составляющие схему учёта банком векселя (рис. 4) Заёмщик решил взять кредит на сумму
По истечении некоторого времени
где
Однако, банк, оказывая услугу по учёту векселя, желает получить комиссионные
При этом
Вычисление средних значений Предоставляя многочисленные кредиты с различными параметрами, кредитор желает знать средние значения ставок, периодов предоставления кредита. Эти параметры являются статистическими значениями, вычисляемыми по совокупности конкретных финансовых сделок. Пусть Для вычисления средних значений
или
Поскольку
из которого следует
Если ввести взвешенную среднюю арифметическую процентную ставку
то среднее время предоставления ссуды составит
Формула (20) определяет среднее время предоставления ссуды в виде взвешенной средней арифметической частных периодов. Если ввести взвешенную среднюю арифметическую процентную ставку
то среде время предоставления ссуды составит
Пусть теперь
Пусть клиент хочет получить ссуду
или при условии
Если положить, что среднее значение учетной ставки
то среднее значение срока предоставления ссуды
Если теперь положить
то
Сравнивая формулы (17 – 22) с соответствующими формулами (23 – 28), замечаем, что они являются симметричными, т.е. получаются заменой Р на F и r на d.
Сложные проценты
Наращение сложных процентов
Для поощрения долгосрочных вкладов клиентов применяют процедуру капитализации процентов, т. е. присоединение начисленных процентов к базе и в дальнейшем начисление процентов на эту сумму. Такая схема процентов называется схемой сложных процентов.
Наиболее простой вид алгоритма наращения по схеме сложных процентов получим, если в формуле (13) положим
В общем случае в формуле (35) число Поучаемые проценты
Если
Замечание. Отвечая на вопрос «Чему равно Ø по схеме простых процентов Ø по схеме сложных процентов
Смешанная схема процентов
Сравнение процессов наращения по схеме простых процентов со схемой сложных процентов показывает, что на временном интервале до 1 года наращенная сумма по схеме простых процентов оказывается больше. Отсюда вывод: кредитор применяет схему сложных процентов на интервалах более 1 года, а простую – на интервалах до 1 года. Если
Тогда исчисление наращенной суммы по формуле
называют смешанной схемойсложных процентов.
Сложная учётная ставка
В момент заключения финансовой сделки начисляются проценты (антисипативные проценты) на долговое обязательство Пусть оно досрочно учитывается с дисконтом по сложной учетной ставке
а продавцу долгового обязательства будет причитаться сумма При учёте долгового обязательства за два года до погашения процент составит
продавцу будет причитаться сумма
Таким образом, сумма продавцу за
а дисконт равен
Таким образом, в момент оформления долгового обязательства на сумму Если
При дисконтировании
Если количество дисконтирования в году увеличивается, то
Если заданы
Эффективная учётная ставка
Так как возможны разные схемы дисконтирования сложных процентов, то знание номинальной учетной ставки не позволяет их сравнивать. Определение. Учётнаяставка, обеспечивающая переход от суммы Применение эффективной ставки должно обеспечивать равносильность схем наращения:
Замечание. Чем выше учётная ставка, тем выше расходы заёмщика по обслуживанию полученной ссуды. Из финансового эквивалента
находим размер эффективной учётной ставки
Обратный переход выполняется по формуле
В контрактах со смешанным способом дисконтирования процентов по известным значениям
Денежные потоки
Оценка аннуитета
Кафедра математических и естественных наук
Клюжев Н.А., Ганго С.Е.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.92.25 (0.008 с.) |

 сумма вклада, хранящаяся неизменной в течение интервала времени
сумма вклада, хранящаяся неизменной в течение интервала времени  .
. 
 . (7)
. (7) . (8)
. (8) на срок
на срок  по процентной ставке
по процентной ставке  . Им был выписан вексель на сумму
. Им был выписан вексель на сумму  к моменту погашению. Эта сумма была вычислена по схеме простых процентов:
к моменту погашению. Эта сумма была вычислена по схеме простых процентов: .
. владелец векселя принял решение учесть в банке (продать банку и получить наличными или положить на счёт для дальнейшего использования). Время до момента погашения векселя равно
владелец векселя принял решение учесть в банке (продать банку и получить наличными или положить на счёт для дальнейшего использования). Время до момента погашения векселя равно  выбирается им в соответствии с выполнением неравенства (6):
выбирается им в соответствии с выполнением неравенства (6): ,
,
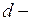 учётная ставка, которую предложил банк владельцу векселя. На момент учёта векселя наращенная стоимость
учётная ставка, которую предложил банк владельцу векселя. На момент учёта векселя наращенная стоимость .
. и проценты
и проценты  , которые в сумме составляют дисконт (скидку)
, которые в сумме составляют дисконт (скидку)  с суммы
с суммы  .
. . Комиссионные за услугу составят
. Комиссионные за услугу составят .
. ,
,  , совокупность долгов с декурсивными процентами, а
, совокупность долгов с декурсивными процентами, а  среднее время предоставления совокупной ссуды
среднее время предоставления совокупной ссуды  , средняя процентная ставка.
, средняя процентная ставка. требуется учесть интересы кредиторов и заёмщиков. Для этих целей составляются финансовые соотношения, имеющие смысл уравнений и называемые финансовыми эквивалентами. В данном случае составляется финансовый эквивалент:
требуется учесть интересы кредиторов и заёмщиков. Для этих целей составляются финансовые соотношения, имеющие смысл уравнений и называемые финансовыми эквивалентами. В данном случае составляется финансовый эквивалент: (16)
(16)
 .
.
 , (17)
, (17)
 . (18)
. (18)
 , (19)
, (19) . (20)
. (20) , (21)
, (21) . (22)
. (22) ,
,  .
. на срок
на срок  под среднюю учетную ставку
под среднюю учетную ставку  . В этом случае финансовый эквивалент
. В этом случае финансовый эквивалент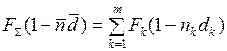 (23)
(23) получим, что
получим, что
 . (24)
. (24)
 , (25)
, (25) . (26)
. (26) , (27)
, (27) . (28)
. (28) :
: ,
,  . (35)
. (35) положительное вещественное число (целое или дробное). Так, если
положительное вещественное число (целое или дробное). Так, если  наращенная сумма за
наращенная сумма за 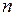 годовых периодов при начальной сумме
годовых периодов при начальной сумме  ссуды при процентной ставке
ссуды при процентной ставке  называется множителем наращения.
называется множителем наращения. . (36)
. (36)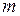 периодов начисления с капитализацией процентов произвольны, но исчисляется каждый целым числом лет
периодов начисления с капитализацией процентов произвольны, но исчисляется каждый целым числом лет  и годовая ставка процентов
и годовая ставка процентов  переменная, то наращенная сумма
переменная, то наращенная сумма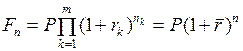 ,
,  , (37)
, (37) .
. ?», получим:
?», получим: ;
; .
. .
. (38)
(38) со сроком погашения
со сроком погашения  . Так за год до срока погашения процент составит
. Так за год до срока погашения процент составит ,
,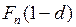 .
.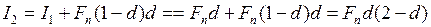 ,
, .
. , (47)
, (47) . (48)
. (48)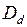 (48) и продавец долгового обязательства получит сумму
(48) и продавец долгового обязательства получит сумму  . (49)
. (49)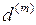
 . (50)
. (50)
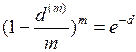 . (51)
. (51) , то срок до погашения долгового обязательства можно вычислить по формуле
, то срок до погашения долгового обязательства можно вычислить по формуле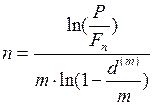 . (52)
. (52) .
. ~
~  .
. (53)
(53) . (54)
. (54) . (55)
. (55)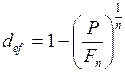 . (56)
. (56)


