
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутригодовые процентные начисленияСодержание книги Поиск на нашем сайте
Вновь вернемся к формуле (13) и запишем её в виде
где
Эффективная годовая процентная ставка
Так как возможны разные схемы начисления сложных процентов, то знание номинальной процентной ставки не позволяет их сравнивать.
Определение. Ставка, обеспечивающая переход от текущей суммы Применение эффективной ставки должно обеспечивать равносильность схем наращения:
Замечание. Чем выше эффективная ставка, тем выше расходы заёмщика по обслуживанию полученной ссуды.
Примеры расчета эффективной ставки: 1) в рамках одного года верно равенство
из которого получаем
В частности,
Обратный переход к номинальной ставке выполняется по формуле:
Определение. Две номинальные ставки называются эквивалентными, если они дают оду и ту же эффективную ставку.
В контрактах со смешанным способом начисления процентов по известным значениям
В США используются номинальные ставки, а в Европе сначала находят эффективную ставку и далее вычисляют наращенную сумму
Дисконтирование по сложной процентной ставке
При решении задачи нахождения по заданному доходу
В этом случае дисконт составляет
При смешанной схеме применяют формулу математического дисконтирования
Сложная учётная ставка
В момент заключения финансовой сделки начисляются проценты (антисипативные проценты) на долговое обязательство Пусть оно досрочно учитывается с дисконтом по сложной учетной ставке
а продавцу долгового обязательства будет причитаться сумма При учёте долгового обязательства за два года до погашения процент составит
продавцу будет причитаться сумма
Таким образом, сумма продавцу за
а дисконт равен
Таким образом, в момент оформления долгового обязательства на сумму Если
При дисконтировании
Если количество дисконтирования в году увеличивается, то
Если заданы
Эффективная учётная ставка
Так как возможны разные схемы дисконтирования сложных процентов, то знание номинальной учетной ставки не позволяет их сравнивать. Определение. Учётнаяставка, обеспечивающая переход от суммы Применение эффективной ставки должно обеспечивать равносильность схем наращения:
Замечание. Чем выше учётная ставка, тем выше расходы заёмщика по обслуживанию полученной ссуды. Из финансового эквивалента
находим размер эффективной учётной ставки
Обратный переход выполняется по формуле
В контрактах со смешанным способом дисконтирования процентов по известным значениям
Наращение сложными процентами по учётной ставке
В общем случае формула наращения сложными процентами по учётной ставке имеет вид:
Сравнение наращений по процентной ставке с наращениями по учётной ставке даёт ответ: наращение по учётной ставке происходит более значительно. Если в обязательстве применялись плавающие учётные ставки, то
где
|
|||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.149.14 (0.01 с.) |

 , (39)
, (39) число процентов начислений в году;
число процентов начислений в году;  годовая ставка, где
годовая ставка, где 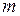 указывает число начислений в год, или номинальная процентная ставка. Тогда обозначив через
указывает число начислений в год, или номинальная процентная ставка. Тогда обозначив через 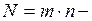 общее число начислений за
общее число начислений за 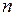 лет, получим формулу наращения за
лет, получим формулу наращения за  . (40)
. (40) к наращенной
к наращенной  при однократном начислении процентов, называется эффективной и обозначается
при однократном начислении процентов, называется эффективной и обозначается  .
. ~
~  .
.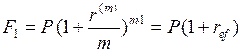 ,
,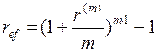 . (41)
. (41)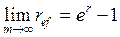 .
. . (42)
. (42) находят эффективную процентную ставку
находят эффективную процентную ставку . (43)
. (43) .
. и в общем случае при
и в общем случае при  кратном начислении применяют формулу:
кратном начислении применяют формулу: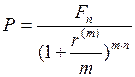 . (44)
. (44)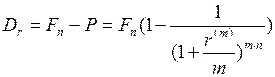 . (45)
. (45) . (46)
. (46) . Так за год до срока погашения процент составит
. Так за год до срока погашения процент составит ,
,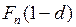 .
.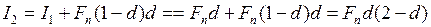 ,
, .
. , (47)
, (47) . (48)
. (48)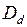 (48) и продавец долгового обязательства получит сумму
(48) и продавец долгового обязательства получит сумму  нецелое число лет, то можно применить смешанную схему учёта:
нецелое число лет, то можно применить смешанную схему учёта: . (49)
. (49)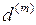
 . (50)
. (50)
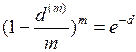 . (51)
. (51) , то срок до погашения долгового обязательства можно вычислить по формуле
, то срок до погашения долгового обязательства можно вычислить по формуле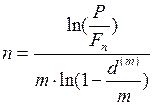 . (52)
. (52) .
. ~
~  .
. (53)
(53) . (54)
. (54) . (55)
. (55)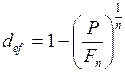 . (56)
. (56)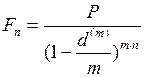 . (57)
. (57)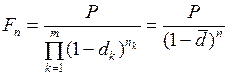 , (58)
, (58) , а средняя учётная ставка
, а средняя учётная ставка . (59)
. (59)


