
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисконтирование по сложной учетной ставкеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В учетных (дисконтных) операциях широко применяется сложная учетная ставка. В этом случае дисконтирование осуществляется по формуле: P` = S*(1-dc)n, где dc – сложная годовая учетная ставка. Дисконт вычисляется как разность: D` = S-P` = S – S*(1-dc)n = S*[1-(1- dc)n] Пример: Владелец долгового обязательства, равного 0,6 млн. руб., со сроком погашения через 2 года сразу же после заключения этого контракта учел его в банке по сложной учетной ставке 9%. Определим сумму, полученную владельцем обязательства, и дисконт, полученный банком. P` = 0,6*(1-0,09)2 = 0,497 млн. руб.; D` = 0,6 – 0,497 = 0,103 млн. руб. Для сравнения рассчитаем по приведенным данным дисконтированную величину P` и дисконтную величину D` с использованием простой учетной ставки: P` = 0.6*(1-0.09)2 = 0.497 млн. руб. D` = 0,6 – 0,497 = 0,103 млн. руб. Зная величины S, P, n можно определить значение сложной учетной ставки (dc): Dc = 1-(P / S)1/n. Пример: Первоначальная сумма (0,5 млн. руб.), помещенная в банк на 2 года, в конце срока выросла до 0,65 млн. руб. Наращение производилось по сложной учетной ставке. Определим величину этой ставки. Dc = 1 – (0.5 / 0.65)1/2 = 0.1229 (или 12, 29 %).
Рентные платежи и их анализ
Ранее рассматривались случаи, когда начисление процентов или дисконтирование производилось по отношению к одноразовому вкладу или ссуде. Между тем оплата по заключенным сделкам может предусматривать как разовый платеж, так и ряд выплат, распределенных во времени. Погашение среднесрочной и долгосрочной банковских задолженностей, коммерческого кредита, инвестирование средств в различные программы, создание денежных фондов целевого назначения и другие платежи в большинстве случаев предусматривают выплаты, производимые через определенные промежутки времени. При этом возникает ряд последовательных платежей, которые обычно именуют потоком платежей. Ряд последовательных фиксированных платежей, производимых через равные промежутки времени, называется рентой или аннуитетом. Аннуитет может быть охарактеризован рядом параметров: 1) член ренты – величина каждого отдельного платежа; 2) период ренты – временной интервал между двумя платежами; 3) срок ренты – время от начала реализации ренты до момента начисления последнего платежа; 4) процентная ставка – ставка, используемая для расчета наращения или дисконтирования, составляющих ренту. На практике используются различные виды рент: - ренты, по которым платежи производятся раз в год – годовые; - платежи, по которым производятся несколько раз (р-раз) в году – р-срочными; - период между платежами может превышать год; Все перечисленные ренты называются дискретными. Наряду с дискретными есть непрерывные ренты, где платежи производятся очень часто. В зависимости от частоты начисления процентов различают ренты с начислением процентов один раз в году, несколько раз в году (m раз) и непрерывным начислением. С точки зрения стабильности размера платежей ренты подразделяются на постоянные и переменные. Рента, выплата которой не ограничена какими-либо условиями, называется верной. Рента, выплата которой обусловлена наступлением какого-либо события, называется условной. Число членов условной ренты заранее предусмотреть невозможно. Примером условной ренты могут служить страховые взносы, вносимые до наступления страхового случая. Ренты могут иметь конечное число членов (ограниченные ренты) и быть с бесконечным числом членов (вечные ренты). Так, например, правительствами ряда стран выпускаются облигационные займы без ограничения срока погашения. Доходы по этим облигациям, выплачиваемые через определенные промежутки времени, являются членами вечной ренты. По моменту выплат членов ренты последние подразделяются на обычные – постнумерандо, в которых платежи производятся в конце соответствующих периодов (года, полугодия и т.д.), и пренумерандо, в которых платежи осуществляются в начале этих периодов. Встречаются также ренты, в которых предусматривается поступление платежей в середине периода. Одним из обобщающих показателей ренты является наращенная сумма. Наращенная сумма – это сумма всех членов потока платежей с начисленными на них процентами на конец срока, т.е. на дату последней выплаты. Наращенная сумма показывает, какую величину будет представлять капитал, вносимый через равные промежутки времени в течение всего срока ренты вместе с начисленными процентами. Обобщающие характеристики ренты используются в финансовом анализе при заключении различных коммерческих сделок, для планирования погашения задолженности, сравнения эффективности контрактов, имеющих различные условия их реализации. Пример: Владелец малого предприятия принял решение создать страховой фонд. С этой целью в течение 5 лет в конце каждого года в банко вносится 200,0 тыс. руб. под 10 % годовых с последующей их капитализацией, т.е. с прибавлением к уже накопленной сумме. Определим наращенную сумму к концу срока ренты. Введем обозначения: R – величина ежегодного взноса; i – процентная ставка; n – срок ренты. Представим эту финансовую операцию в виде таблицы:
Как видно из таблицы, на вносимые платежи в течение всего срока ренты начисляются проценты в следующем порядке: На 1-й взнос 4 раза: R*(1+i)4 = R*(1+i)n-1 На 2-й взнос три раза: R*(1+i)3 = R*(1+i)n-2 На 3-й взнос два раза: R*(1+i)2 = R*(1+i)n-3 На 4-й взнос один раз: R*(1+i) = R*(1+i)n-4 На 5-й взнос проценты не начисляются: R. Наращенная сумма к концу срока ренты составит сумму членов этого ряда, который, если его переписать в обратном порядке, является возрастающей геометрической прогрессией, где R – 1-й член прогрессии, а величина (1+i) – знаменатель прогрессии. Тогда сумму членов ряда, т.е. наращенную сумму ренты, можно определить по формуле: S = R* Величина Обозначим коэффициент наращения Sn,j, где подстрочные символы указывают на срок ренты и применяемую процентную ставку соответственно. Тогда формула примет вид: S = R*Sn,j Значения коэффициента наращения табулированы, что облегчает ведение расчетов. По данным примера рассчитаем наращенную сумму ренты: S = 200,0* Эту же величину можно получить, выбрав по специальной таблице коэффициент наращения рент. Если рентные платежи вносятся раз в году, а проценты на них начисляются несколько раз в году (m раз в году), то начисление процентов каждый раз будет производиться по ставке j/m, где j – номинальная годовая ставка сложных процентов. Величина наращенной суммы будет определяться по формуле: S = R* где n – срок ренты в годах. Пример: Страховая компания, заключившая договор с производственной фирмой на 3 года, поступающие ежегодные страховые взносы – 500,0 тыс. руб. помещает в банк под 15 % годовых с начислением процентов по полугодиям. Определим сумму, полученную страховой компанией по этому договору. Сумма, полученная страховой компанией, составит S = 500* Расчет наращенной суммы при начислении процентов m раз в году можно производить с помощью табулированных коэффициентов наращения Sm*n; j/m и Sm,j/m. Для этого воспользуемся соотношением:
где m – число периодов начисления процентов в течение года; n – срок ренты; j – номинальная ставка. В этом случае наращенная сумма определяется по формуле: S = R* По специальной таблице находим: S = 500*7.24402 / 2.0750 = 1745, 5 тыс. руб. Рентные платежи могут вносится несколько раз в году равными суммами (р-срочная рента), а начисление процентов производится раз в году, в конце года (m = 1). Тогда годовой платеж равен R, первый член ренты – R / P, а коэффициент наращения определяется по формуле: S = R*Sn;j(p) Пример: Страховая компания принимает установленный годовой страховой взнос дважды в год по полугодиям в размере 250 тыс. руб. каждый в течение 3 лет. Банк, обслуживающий страховую компанию, начисляет ей проценты из расчета 15 % годовых (сложные проценты) один раз в году; R = 5,0; n = 3; p = 2; m = 1. Определим сумму, полученную страховой компанией по истечении срока договора. Сумма составит: S = 500*
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.36.45 (0.006 с.) |

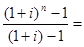 R*
R* 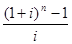 .
.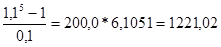 тыс. руб.
тыс. руб. ,
,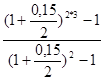 =1745,5 тыс. руб.
=1745,5 тыс. руб.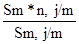 ,
,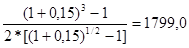 тыс. руб.
тыс. руб.


