
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погашение потребительского кредита изменяющимися суммамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При погашении кредита изменяющимися суммами возникает задача определения суммы, идущей на погашение основного долга, и суммы процентных платежей. Для решения этого вопроса можно воспользоваться «правилом 78». Название этого правила вызвано тем, что сумма порядковых номеров месяцев года равна 78(1 + 2 + 3 +... + 12 = 78). В соответствии с этим правилом уплата процентов при первом платеже составит Иначе говоря, процентные платежи являются убывающей арифметической прогрессией, сумма членов которой определяется по формуле: Sn = Где а1 – первый член прогрессии; an – последний член; n – число членов; d – разность членов прогрессии. При выдаче ссуды на n лет из условия m погасительных платежей в году последовательные номера месяцев за весь период погашения могут быть записаны в обратном порядке следующим образом: t1 = m*n; t2 = m*n – 1; t3 = m*n – 2; tn =1. Сумма этих чисел по формуле арифметической прогрессии будет равна: Q = В каждом платеже доля порядкового числа данного месяца составит
где I – сумма всех процентных платежей; P – первоначальная сумма долга; i – процентная ставка, выраженная десятичной дробью. Сумма погашенного долга на конец периода К равна: Wk = Yk - Где Wk - сумма погашенного долга на момент К; Yk – оставшаяся часть непогашенного долга на момент К. {Задача. Автомобиль стоимостью 252,0 тыс. руб. продан в кредит под 15% годовых (проценты простые). Погашение задолженности производится ежемесячными платежами в течение 2 лет. Составьте план погашения задолженности. Наращенная сумма долга в конце периода равна S= 252(1 +2*0,15) = 327,6 тыс. руб. Сумма начисленных процентов: I = P*n*i = 252 * 2 * 0,15 = 75,6. Ежемесячные выплаты (выплаты основного долга и процентов): q = По условию: m = 12, n = 2, откуда t1 = 24; t2 = 23; t3 = 22;…;t24= 1 Сумма месячных порядковых номеров равна:
Из первого платежа в счет уплаты процентов от общей суммы начисленных процентов идет 24/300, т.е. 24/300 * 13,65 = 1,092 тыс. руб. Сумма, идущая на погашение основного долга в этом месяце, составит 13,65 - 1,092 = 12,558 тыс. руб.
Следовательно, остаток основного долга на начало следующего месяца равен 252,0 - 12,558 = 239,442 тыс. руб. Во втором месяце сумма, идущая на погашение процентов, составит 23/300*13,65 = 1,0465 тыс. руб. и т.д. В таблице показаны (с рядом пропусков) расчеты, представляющие основу плана погашения долга. План погашения долга
Наряду с рассмотренными способами воспользуемся способом, когда процентный платеж рассчитывается методом счета «от ста». При этом процентный платеж за пользование потребительским кредитом начисляется предварительно: для первого месяца (периода) процентный платеж рассчитывается на всю величину долга, а в каждый следующий месяц – на оставшуюся часть долга, т.е. на величину долга, уменьшенную на уже выплаченную часть; сам же долг выплачивается равными долями. Предположим, что величина кредита равна P и он должен выплачиваться равными месячными платежами m раз с начислением процентов по годовой ставке i. Тогда процентный платеж для первого месяца: I1 = Во втором месяце: I2 = (P-
В третьем месяце: I3 = (P-2* В месяце m: Im Для определения общей величины процентных выплат за предоставленный кредит просуммируем их месячные значения: I = Откуда: I = где При ежемесячной выплате кредита равными долями ее величина будет равна: q = Задача1. Предоставлен потребительский кредит в размере 18000 руб. на срок 6 месяцев под 12% годовых с ежемесячным погашением. Составим план погашения кредита. Ежемесячная выплата основного долга:
Средняя величина ежемесячных взносов: q =
Представим план погашения в табличной форме:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 725; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.255.51 (0.009 с.) |

 общей начисленной суммы процентов, а оставшаяся часть платежа пойдет на уплату основного долга. При втором платеже на оплату процентов пойдет
общей начисленной суммы процентов, а оставшаяся часть платежа пойдет на уплату основного долга. При втором платеже на оплату процентов пойдет  общей начисленной суммы процентов и т.д.
общей начисленной суммы процентов и т.д. или Sn =
или Sn =  .
.
 . Абсолютная величина процентного платежа в каждом платежном периоде будет равна:
. Абсолютная величина процентного платежа в каждом платежном периоде будет равна: ,
,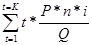 ,
,


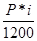 ;
;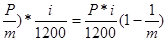

 =
=  =
= 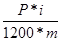


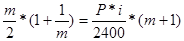 ,
, - процентный коэффициент.
- процентный коэффициент.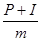 .
.
 руб.
руб. руб.
руб.
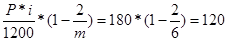



 =
= 
 руб.
руб.


