
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление наращенных сумм на основе простых процентных ставокСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
По условиям кредитного контракта начисленные проценты могут выплачиваться кредитору или по мере их начисления в каждом периоде, или совместно с основной суммой долга по истечении срока контракта. В последнем случае сумма, получаемая кредитором называется наращенной суммой. Наращенная сумма с использованием простых процентов рассчитывается: S = P + I = P + P*n*i = P* (1+n*i), (4) где (1+n*i) – множитель наращения простых процентов. При использовании простых процентов, когда срок финансовой сделки не равен целому числу лет, периоды начисления процентов выражают дробным числом как отношение числа дней функционирования сделки к числу дней в году: n = где t – число дней функционирования сделки (число дней, на которое предоставили кредит); К – временная база (число дней в году). В этом случае формула (4) примет вид: S = P + I = P*(1+ В ряде стран для удобства вычислений год делится на 12 месяцев, по 30 дней в каждом, т.е. продолжительность года (К) принимается равной 360 дням. Это так называемая германская практика. Проценты, рассчитанные с временной базой К = 360 дней, называются обыкновенными или коммерческими (обыкновенные проценты с приближенным числом дней ссуды). Существует французская практика, когда продолжительность года принимается равной 360 дням, а продолжительность месяцев в днях соответствует календарному исчислению. Такой метод начисления процентов называют обыкновенными процентами с точным числом дней ссуды. В ряде стран используется также английская практика, учитывающая продолжительность года в 365 дней, а продолжительность месяцев – в днях, также соответствующих календарному исчислению (точные проценты с точным числом дней ссуды). В этой связи различают три метода процентных расчетов, которые зависят от выбранного периода начисления. 1. Точные проценты с точным числом дней ссуды («английская практика»). При этом методе определяется фактическое число дней (t) между двумя датами (датой получения и погашения кредита), продолжительность года принимается равной К= 365 (366) дней. В этом случае применяется обозначение 365/365. 2. Обыкновенные проценты с точным числом дней ссуды («французская практика»); величина t рассчитывается, как и в предыдущем случае. В этом случае применяется обозначение 365/360. 3. Обыкновенные проценты с приближенным числом дней ссуды («германская практика»); величина t определяется количеством месяцев по 30 дней в каждом начиная с момента выдачи ссуды и до момента ее погашения и точным числом дней ссуды в неполном месяце; продолжительность года К = 360 дней. В этом случае применяется обозначение 360/360. При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимаются за 1 день. Задача 3. Банк выдал районной администрации ссуду в размере 4.0 млн. руб. сроком на 2 года по ставке простых процентов, равной 11% годовых. Определите проценты и сумму накопленного долга (наращенную сумму). Задача 4. Банк выдал кредит 18 января в размере 500,0 тыс. руб. Срок возврата кредита – 3 марта; процентная ставка – 12,0% годовых; год не високосный. Определите сумму долга, подлежащую возврату. Рассчитайте ее тремя методами.
Между величинами процентного дохода, рассчитанными с использованием различной временной базы (I360 и I365), при равном числе дней ссуды (t) существуют следующие соотношения:
Данные соотношения характеризуют зависимость величины процентного дохода от выбранной временной базы. По данным предыдущего примера I360 = 507,33 - 500 = 7,33 тыс. руб.; I365 = 7,23 тыс. руб.;
Эти соотношения также могут быть использованы при определении эквивалентных процентных ставок, т.е. ставок, приносящих одинаковые процентные доходы при различных временных базах, но равных первоначальных капиталах: i360 = 0,9863*i365; i365 = 1.01388*i360. { Выдана ссуда в размере 500,0 тыс. руб. на 15 дней по ставке 12% годовых, при К = 360 дней. Определите наращенную сумму и процентный доход, а также величину процентной ставки, обеспечивающей такой же процентный доход при временной базе К = 365 дней. S = 500*(1+15/360*0,12)=502,5 тыс. руб. I = 2,5 тыс. руб. i365 = 1,01388*0,12 = 0,1216656 Проверим это вычисление: S = 500*(1+15/365*0,1216656) = 502,5 тыс. руб.} При заключении кредитного соглашения может быть установлена постоянная на весь период процентная ставка или изменяющаяся (переменная) процентная ставка. При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная сумма определяется по формуле: S = P*(1+n1*i1+ n2*i2+…+ nt*it) = P*(1+ где it – ставка простых процентов в периоде t; nt – продолжительность начисления ставки it; m – число периодов начисления процентов. Наряду с рассмотренным методом процентных начислений иногда прибегают к начислению процентов на уже наращенные в предыдущем периоде суммы, когда происходит многоразовое наращение, именуемое реинвестированием или капитализацией процентного дохода. В этом случае итоговая наращенная сумма определяется по формуле: S = P *(1+ n1*i1)*(1+ n2*i2)*…*(1+ nt*it), n1, n2,…, nt – продолжительность периодов наращения; i1,i2,…,it – процентные ставки, по которым производится реинвестирование. { Задача 1. Банк предлагает вкладчикам следующие условия по срочному годовому депозиту: в первое полугодие процентная ставка 12,0% годовых, каждый следующий квартал ставка возрастает на 0,5%. Проценты начисляются только на первоначально внесенную сумму вклада. Определите наращенную за год сумму, если вкладчик поместил в банк на этих условиях 400,0 тыс. руб. Задача 2. Клиент поместил в банк 500,0 тыс. руб. Какова будет наращенная за 3 месяца сумма вклада, если за первый месяц начисляются проценты в размере 15% годовых, а каждый последующий месяц процентная ставка возрастает на 1,5% с одновременной капитализацией процентного дохода?
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.233.69 (0.007 с.) |

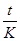 ,
,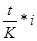 ). (5)
). (5)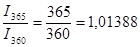 и
и 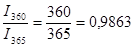 . (6)
. (6)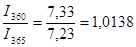 и
и 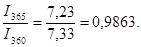
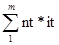 ),
),


