
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. 1. Индекс цен и темп инфляции. Влияние инфляции на доходность. Формула фишера. Индексация первоначальной сумм в условиях инфляции. Методы расчета наращенных сумм в условиях инфляции.Содержание книги
Поиск на нашем сайте
Вопросы для рассмотрения: 1. Инфляция и ее измерения. Индекс потребительских цен. 2. Номинальная и реальная ставки процентов. 3. Расчет наращенных сумм в условиях инфляции. 4. Измерение реальной доходности финансовой операции. Инфляция – устойчивый рост среднего уровня цен на товары и услуги в экономике. Внешние признаки инфляции – рост цен и, как следствие, снижение покупательной способности денег. В зависимости от уровня инфляции в год выделяют: нормальную (ползучую) – от 3% до 10%; галопирующую – от 10% до 100%; гиперинфляцию – свыше 50% в месяц. Темпы инфляции определяются с помощью индекса – относительного показателя, характеризующего среднее изменения уровня цен некоторого фиксированного набора товаров и услуг за данный период времени. Индекс инфляции показывает во сколько раз выросли цены (
Индекс потребительских цен (ИПЦ) – это показатель международной статистики, регулярно использующийся практически во всех странах мира (CPI – Consumer Price Index), который характеризует динамику затрат на постоянный набор товаров и услуг за счет ценностного фактора. Расчет ИПЦ в России осуществляется за каждый месяц и нарастающим итогом с начала года (к декабрю прошлого года). Отечественные исследователи часто расценивают уровень инфляции как темп прироста потребительских цен: τ = ИПЦ – 100 (%) ИПЦ оценивает изменение стоимости фактического фиксированного набора товаров и услуг в отчетном периоде по сравнению с его стоимостью в базисном периоде. Чтобы определить темп инфляции за период t по данным о значении этого показателя за более короткие промежутки рассматриваемого периода необходимо: − Перейти от приростного показателя за короткие промежутки к показателям темпа роста цен. Пример: темп инфляции по кварталам: α1 = 4%; α2 = 3%; α3 = 2%; α4 = 5%; определим темп роста цен: 104%, 103%, 102%, 105%; − Перейти от темпа роста к коэффициенту роста: К21 = 104/100 = 1,04; тК22 = 103/100 = 1,03; К23 = 102/100 = 1,02; К24 = 105/100 = 1,05; − Определить годовой коэффициент роста цен: перемножим коэффициенты за исследуемые периоды: К2год = 1,147 → ТР2год = 114,7% − Темп инфляции за год: ТР2год – 100% = 14,7% Индекс цен за несколько периодов n, следующих друг за другом, вычисляется по формуле
Интерпретация: 1. индекс цен 2. темп роста цен 3. темп прироста цен – уровень инфляции 4. инфляция за год равна произведению индексов цен. Инфляционные процессы, характерные для экономики многих стран, требуют того, чтобы они учитывались в финансовых расчетах. Особенно необходимо рассчитывать воздействие инфляции при вычислении наращенных сумм и определении действительной ставки процентов. Определение действительной ставки процентов Показатели финансовой операции могут быть представлены, как: − номинальные, т.е. рассчитанные в текущих ценах; − реальные, т.е. учитывающие влияние инфляции, и рассчитанные в сопоставимых ценах базисного периода. В связи с этим вводится понятие номинальная ставка процента, т.е. ставки с поправкой на инфляцию (i инф). Простые проценты. Наращенная сумма при отсутствии инфляции равна Это ставка, скорректированная на инфляцию, называется брутто-ставкой. Сложные проценты. Проценты 1 раз в год: Наращенная сумма при отсутствии инфляции равна Проценты m раз в год: При начислении процентов несколько раз в год:
Эти модели позволяют производить учет инфляции и корректировку процентных ставок. Годовая ставка сложных процентов, обеспечивающая реальную доходность кредитной операции, определяется по формуле Фишера, связывает три показателя: R – номинальная процентная ставка, α – уровень инфляции r – реальная процентная ставка (доходность финансовой операции)
Пример 4.1. Годовой темп инфляции 20%. Банк рассчитывает получить 10% реального дохода в результате предоставления кредитных ресурсов. Какова номинальная ставка, по которой банк предоставит кредит?
На практике довольно часто довольствуются сравнением i и τ путем вычисления реальной ставки, т.е. уменьшенной ставки доходности на уровень инфляции: i = (i - τ) / (1 + τ) Поскольку покупательная способность денег снижается в условиях инфляции, то происходит обесценивание денежных доходов. Поэтому при наращении денег на депозите вкладчик должен сопоставить номинальную процентную ставку, т.е. ставку, указанную в договоре, с величиной индекса потребительских цен. Вычисление наращенных сумм Получаем формулу: Реальная стоимость С суммы S, обесцененная во времени за счет инфляции при индексе цен Если наращение производится по простой ставке в течение n лет, то Для определения реальной покупательской способности, наращенную сумму необходимо привести ее к ценам базового периода: Вследствие начисления процентов происходит увеличение денежных сумм, но их стоимость под влиянием инфляции уменьшается. Поскольку каждая денежная единица обесценивается вследствие инфляции, то в дальнейшем обесцениваются уже обесцененные деньги. Наращение осуществляется по простым или сложным процентам, но инфляция всегда оценивается по сложному проценту. Наращенная сумма за n лет с учетом ее обесценивания составит: − Если темп инфляции больше ставки начисляемых процентов, то полученная наращенная сумма не компенсирует потерю покупательной способности денег. Банковская ставка называется отрицательной. − Если темп инфляции меньше ставки начисляемых процентов, то наблюдается реальный рост покупательной способности денег. Банковская ставка называется положительной. − Если темп инфляции равен ставке начисляемых процентов, то покупательная способность наращенной суммы равна покупательной способности первоначальной суммы. Вопросы для самопроверки: 1. Что такое инфляция? Перечислите виды инфляции. 2. Что такое ИПЦ? 3. С какой целью проводят учет инфляции? 4. Что такое номинальная ставка процента? Чем она отличается от реальной ставки? 5. Что такое финансовая операция? 6. Как измерить реальную доходность финансовой операции? Тема 5.1.-5.2. Понятия видов потоков платежей и их основные параметры. Понятие финансовой ренты. Основные параметры ренты и их вычисление. Различные виды финансовых рент. Виды переменных рент. Постоянная непрерывная рента. Конверсии рент. Вопросы для рассмотрения: 1. Ренты. Классификация рент. 2. Наращенная сумма финансовой ренты постнумерандно. 3. Современная величина финансовой ренты постнумерандно. 4. Срок финансовой ренты постнумерандно. 5. Член финансовой ренты постнумерандно. 6. Наращенная сумма и современная величина других типов финансовых рент. 7. Определение параметров других типов финансовых рент. 8. Определение процентной ставки финансовой ренты.
Очень часто в контрактах финансового характера предусматриваются не отдельные разовые платежи, а серию платежей, распределенных во времени. Примерами могут быть регулярные выплаты с целью погашения долгосрочного кредита вместе с начисленными на него процентами, периодические взносы на расчетный счет, на котором формируется некоторый фонд различного назначения (инвестиционный, пенсионный, страховой, резервный, накопительный и т.д.), дивиденды, выплачиваемые по ценным бумагам, выплаты пенсий из пенсионного фонда и пр. Ряд последовательных выплат и поступлений называют потоком платежей. Выплаты представляются отрицательными величинами, а поступления - положительными. Обобщающими характеристиками потока платежей являются наращенная сумма и современная величина. Каждая из этих характеристик является числом. Наращенная сумма потока платежей - это сумма всех членов последовательности платежей с начисленными на них процентами к концу срока ренты. Под современной величиной потока платежей понимают сумму всех его членов, дисконтированных (приведенных) на некоторый момент времени, совпадающий с началом потока платежей или предшествующий ему. Конкретный смысл этих обобщающих характеристик определяется природой потока платежей, причиной, его порождающей. Например, наращенная сумма может представлять собой итоговый размер формируемого инвестиционного или какого-либо другого фонда, общую сумму задолженности. Современная величина может характеризовать приведенную прибыль, приведенные издержки. 5.1. Понятие финансовой ренты (аннуитета) Поток платежей, все члены которого положительные величины, а временные интервалы постоянны, называют финансовой рентой или аннуитетом. Финансовая рента имеет следующие параметры: член ренты - величина каждого отдельного платежа, период ренты - временной интервал между двумя соседними платежами, срок ренты - время, измеренное от начала финансовой ренты до конца ее последнего периода, процентная ставка - ставка, используемая при наращении или дисконтировании платежей, образующих ренту, число платежей в году, число начислений процентов в году, моменты платежа внутри периода ренты. Виды финансовых рент Классификация рент может быть произведена по различным признакам. Рассмотрим их. В зависимости от продолжительности периода, ренты делят на годовые и p-срочные, где p - число выплат в году. Довольно часто в практике встречаются ренты, в которые период выплат превышает год и более (например, в инвестиционной деятельности). По числу начислений процентов различают ренты с начислением один в году, m раз или непрерывно. Моменты начисления процентов могут не совпадать с моментами рентных платежей. По величине членов различают постоянные (с равными членами)и переменные ренты. Если размеры платежей изменяются по какому-либо математическому закону, то часто появляется возможность вывести стандартные формулы, значительно упрощающие расчеты. По вероятности выплаты членов различают ренты верные и условные. Верные ренты подлежат безусловной выплате, например, при погашении кредита. Выплата условной ренты ставится в зависимость от наступления некоторого случайного события. Поэтому число ее членов заранее неизвестно. Например, число выплат пенсий зависит от продолжительности жизни пенсионера. По числу членов различают ренты с конечным числом членов или ограниченные и бесконечные или вечные. В качестве вечной ренты можно рассматривать выплаты по облигационным займам с неограниченными или не фиксированными сроками. Так, например, с необходимостью учета и расчета вечной ренты приходится сталкиваться при финансовых вычислениях, связанных с инвестированием денежных средств или покупкой финансового инструмента (материального объекта), если период их функционирования (возможного получения дохода) достаточно продолжительный и не оговорен конкретными сроками (отсюда и возможность получения бессрочной, т.е. «вечной» ренты), в качестве примера можно привести инвестирование в ценные бумаги крупнейших транснациональных компаний и государства (при отсутствии срока окончания их обращения), покупку доходных гостиниц, ферм, участков земли, производств и т.п. В зависимости от наличия сдвига момента начала ренты по отношению к началу действия контракта или какому-либо другому моменту ренты подразделяются на немедленные и отложенные или отсроченные. Срок немедленных рент начинается сразу, а у отложенных запаздывает. Ренты различают по моменту выплаты платежей. Если платежи осуществляются в конце каждого периода – года, полугодия, месяца и т.п., то такие ренты называются обычными или постнумерандо. Если же выплаты производятся в начале каждого периода, то ренты называются пренумерандо. Иногда предусматриваются платежи в середине каждого периода. постнумерандо(когда платежи осуществляются в конце соответствующих периодов) и ренты пренумерандо(когда соответствующие платежи осуществляются в начале указанных периодов). Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования. Рента пренумерандо отличается от обычной ренты числом периодов начисления процентов. Поэтому наращенная сумма ренты пренумерандо будет больше наращенной суммы обычной ренты в (1 + i) раз. Нечасто, но встречаются на практике и ренты, платежи по которым производятся в середине периодов. Такие ренты называются миннумерандо. Примером такой ренты могут служить, в ряде случаев, авансовые платежи по аренде помещений, а также полугодовые оплаты трат по внешнеторговым контрактам. Чаще всего в практических финансово-экономических расчетах решается, по существу, двуединая задача определения наращенной суммыили современной величины(стоимости) потока платежей. В данном контексте под современной величиной потока платежей понимается сумма всех его членов, дисконтированных на некоторый момент времени, совпадающий с началом потока платежей, или упреждающий его. Она может характеризовать капитализированный доход, чистую приведенную прибыль, приведенные издержки, эффективность инвестиций и валютно-финансовых условий внешнеторговых контрактов, доходность вкладов и депозитов и др. финансово-экономических и коммерческих операций. Формулы наращенной суммы Обычная годовая рента Пусть в конце каждого года в течение n лет на расчетный счет вносится по R рублей, проценты начисляются один раз в года по ставке i. В этом случае первый взнос к концу срока ренты возрастет до величины
где
Пример: В течение 3 лет на расчетный счет в конце каждого года поступает по 10 млн. руб., на которые начисляются проценты по сложной годовой ставке 10%. Требуется определить сумму на расчетном счете к концу указанного срока. Решение:
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 4217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.008 с.) |

 ), а темп инфляции показывает, насколько процентов возросли цены (τ), т.е. по своей сути это соответственно темп роста и темп прироста:
), а темп инфляции показывает, насколько процентов возросли цены (τ), т.е. по своей сути это соответственно темп роста и темп прироста: = 1 + τ.
= 1 + τ. где i – номер периода;
где i – номер периода; 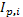 – индекс цен в периоде i;
– индекс цен в периоде i;  – темп инфляции в периоде i.
– темп инфляции в периоде i.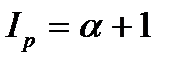 ;
; ;
; ;
;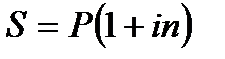 , а ее эквивалент в условиях инфляции равен
, а ее эквивалент в условиях инфляции равен  . Из равенства:
. Из равенства:  получаем:
получаем:  , где i – простая ставка процентов, характеризующая требуемую реальную доходность финансовой операции (нетто-ставка); i τ – процентная ставка с поправкой на инфляцию.
, где i – простая ставка процентов, характеризующая требуемую реальную доходность финансовой операции (нетто-ставка); i τ – процентная ставка с поправкой на инфляцию.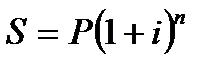 , а ее эквивалент в условиях инфляции равен
, а ее эквивалент в условиях инфляции равен  . Из равенства:
. Из равенства:  получаем:
получаем:  из которой можно сравнивать уровни процентной ставки и инфляции, проводить анализ эффективности вложений и устанавливать реальный прирост вложенного капитала.
из которой можно сравнивать уровни процентной ставки и инфляции, проводить анализ эффективности вложений и устанавливать реальный прирост вложенного капитала.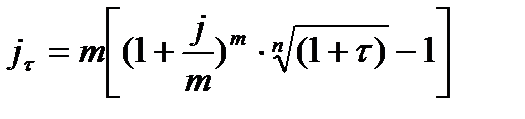 .
. ,
,  ,
,  .
. , R=0,32=32%
, R=0,32=32% или
или  , где
, где  -уровень инфляции.
-уровень инфляции. , рассчитывается по формуле:
, рассчитывается по формуле: 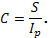
 . С учетом инфляции реальная стоимость суммы S составит
. С учетом инфляции реальная стоимость суммы S составит 
 .
. , здесь множитель наращения, учитывающий темп инфляции.
, здесь множитель наращения, учитывающий темп инфляции.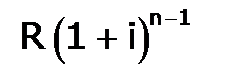 , так как на сумму R проценты начислялись в течение n-1 года. Второй взнос увеличится до
, так как на сумму R проценты начислялись в течение n-1 года. Второй взнос увеличится до  и т.д. На последний взнос проценты не начисляются. Таким образом, в конце срока ренты ее наращенная сумма будет равна сумме членов геометрической прогрессии
и т.д. На последний взнос проценты не начисляются. Таким образом, в конце срока ренты ее наращенная сумма будет равна сумме членов геометрической прогрессии , в которой первый член равен R, знаменатель (1+i), число членов n. Эта сумма равна
, в которой первый член равен R, знаменатель (1+i), число членов n. Эта сумма равна , (1.1)
, (1.1) - по схеме постнумерандо.
- по схеме постнумерандо.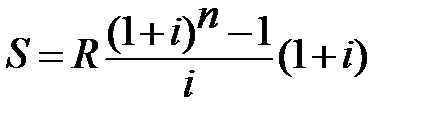 - по схеме пренумерандо. (1.2)
- по схеме пренумерандо. (1.2) млн. руб.
млн. руб.


