
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчеты по стандартным ипотечным ссудам
Наиболее распространенной является ипотечная ссуда, условия которой предполагают равные взносы должника. Взносы ежемесячные — постнумерандо или пренумерандо. В договоре обычно устанавливается ежемесячная ставка процента, редко — годовая номинальная. В осуществлении ипотеки при покупке (строительстве) объекта залога участвуют три агента: продавец, покупатель (должник), заимодавец (кредитор). Взаимосвязи между ними показаны на. рис. 8.1.
Продавец получает от покупателя за некоторое имущество полную его стоимость (120). Для того чтобы расплатиться, покупатель получает ссуду под залог этого имущества (100) и добавляет собственные средства (20). Задача заключается в определении размера ежемесячных погасительных платежей R и остатка задолженности на момент очередного ее погашения вплоть до полного погашения долга. Поскольку погасительные платежи (взносы) представляют собой постоянную ренту, при решении поставленной задачи применим тот же принцип, что и при разработке плана погашения долгосрочного долга равными срочными уплатами. Для этого приравняем современную величину срочных уплат сумме ссуды. Для месячных взносов постнумерандо находим: D = RaN;i, где D — сумма ссуды; N — общее число платежей, N = 12 n (n — срок погашения вгодах); i — месячная ставка процента; R — месячная сумма взносов; aN;i — коэффициент приведения постоянной ренты. Искомая величина взноса составит:
В рамках решаемой проблемы величину с = 1/ aN;i можно назвать коэффициентом рассрочки. Для рент пренумерандо получим:
Найденная по формуле (8.1) или (8.2) величина срочной уплаты является базой для разработки плана погашения долга. Согласно общепринятому правилу из этой суммы выплачиваются проценты, а остаток идет на погашение долга. Пример 8.1. Под залог недвижимости выдана на десять лет ссуда в размере 100 млн. руб. Погашение ежемесячное, постнумерандо, на долг начисляются проценты по номинальной годовой ставке 12%. Таким образом, N = 120, i = 0,01; по формуле (8.1) находим a I20;1 = 69,70052. Для этих условий ежемесячные расходы должника равны: R = Проценты за первый месяц равны 100 000 х 0,01 = 1000 тыс. руб., на погашениедолга остается 1434,71 - 1000 = 434,71 тыс. руб. План погашения долга представлен в табл. 8.1.
Таблица 8.1
Как показано в таблице, в первом месяце расходы на выплату процентов и погашение основного долга соотносятся как 1000: 434,71; в последнем месяце — уже как 14,21: 1420,5. Перейдем к другой проблеме. При выдаче ссуды под залог для обеих сторон важно знать сумму погашенного долга и его остаток на любой промежуточный момент (необходимость в этом возникает, например, при прекращении договора или его пересмотре). С этой проблемой мы уже встречались выше при обсуждении метода погашения долга равными срочными уплатами. Применительно к условиям стандартной ипотеки находим следующие соотношения: dt = dt- 1(1 + i) = d 1(1 + i) t- 1, где dt — сумма погашения долга; t — порядковый номер месяца; i — месячная ставка процента. Остаток долга на начало месяца: Dt - 1= Dt - dt; t = 1,..., 12 n. Последовательные суммы погашения долга представляют собой геометрическую прогрессию с первым членом d 1 и знаменателем (1 + i), причем: d 1 = R - Di (8.3) Сумму членов этой прогрессии от начала погашения до t включительно найдем следующим образом: Wt = d 1 st;i, (8.4) где st;i — коэффициент наращения постоянной ренты постнумерандо. Остаток долга на начало месяца находим как разность: Dt+ 1= D 1 - Wt. (8.5) Пример 8.2. По условиям ипотечного займа примера 8.1 найдем остаток долга на начало, скажем, 118-го месяца: D 118= D 1 - W 117; W 117 = d 1 s 117;1 = 434,71 х 220,3329 = 95780,65. Отсюда D 118 = 100000 - 95780,65 = 4219,35 тыс. руб. Стандартная ипотека с неполным погашением задолженности и выплатой в конце срока остатка долга (balloon mortgage). Условия такой ипотеки позволяют уменьшить размеры периодических взносов и (или) сократить срок ссуды. Срочные уплаты рассчитываются таким образом, что они не покрывают всей задолженности, остаток (обозначим его как В)выплачивается в конце срока. Уравнение, балансирующее условия ипотеки, имеет вид:
D = RaN;i + BvN. Баланс достигается одним из следующих способов: • задается размер срочных уплат, определяется величина В; • задается В,определяется размер срочныхуплат. Решение получим с помощью следующих формул:
Далее расчет ведется по уже рассмотренной схеме.
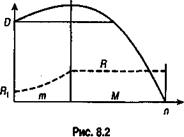
Нестандартные ипотеки Ипотека с ростом платежей (GRM). Общая схематакой ссуды в основном не отличается от стандартной. Различие лишь в том, что первый взнос минимален, затем на некотором начальном интервале времени (пять - десять лет) они увеличиваются с постоянным темпом, далее они постоянны. Как уже отмечено выше, в первые годы текущие расходы должника могут оказаться меньше, чем суммы начисленных процентов. В этом случае основная сумма долга некоторое время будет увеличиваться — см. рис. 8.2.
Разделим весь срок погашения ссуды на два интервала протяженностью т и М месяцев. В первом периоде расходы растут с постоянным темпом роста g. Rt = R 1 gt- 1, где R 1 - расходыв первом месяце; g - ежемесячный темп роста расходов. Во втором периоде расходы должника равны постоянной величине R = R1gm- 1. (8. 6) Найдем современную стоимость платежей каждого периода относительно начала действия контракта. Поскольку в первом периоде последовательность платежей представляет собой геометрическую прогрессию, то искомая величина находится(см. формулу 5.14) как
Во втором периоде платежи представляют собой отложенную постоянную ренту с членом R. На начало действия контракта современная стоимость этой ренты определяется как A 2 = RaM;iv m = R 1 gm- 1 aM;iv m. (8.8) Приравняем современную стоимость всего потока платежей к сумме задолженности, после чего, использовав формулы (8.6) - (8.8) и выполнив ряд преобразований, находим:
Пример 8.3. Сумма задолженности по договору ипотеки — 100 млн. руб., общий срок погашения — 20 лет (240 месяцев); предусматривается рост платежей в течение 60 месяцев; процентная ставка за ссуду — 10% годовых; ежегодный прирост платежей — 5%. Необходимо разработать график погашения. Исходные данные: m = 60, M = 180, i = 0,1 / 12 = 0,08333, v = 0,991735, ежемесячный темп роста расходов в первом периоде составит: g = На основе приведенных данных по формуле (8.9) находим: R = 802,87 тыс. руб. Таким образом, ежемесячные расходы в первом периоде определяются как 802,87 х 1,004074 t - 1. Например, расходы в конце пятилетнего периода равны: R = 802,87 х 1,00407460 - 1 = 1020,52 тыс. руб. Эта же сумма ежемесячно выплачивается во втором периоде (см. табл. 8.2). Таблица 8.2
Таблица 8.2 (продолжение)
Как видим, сумма начисленных процентов в первом периоде меньше взноса. Адекватно увеличивается сумма долга. Максимальная сумма долга приходится на начало одиннадцатого месяца. Начиная с одиннадцатого месяца взносы превышают сумму процентов.
Ссуда с периодическим увеличением взносов. В этом варианте ипотеки задается последовательность размеров взносов. Пусть увеличение взносов происходит через равные интервалы времени т. Очевидно, что для полной сбалансированности схемы размер последнего взноса не задается, он определяетсяпо сумме остатка задолженности. Обозначим размеры взносовкак R 1,..., Rk. Определим размер последнего взноса. Для этого найдем сумму современных стоимостей взносов от первого до k - 1 на начало операции. Обозначим ее как Q.
Современная стоимость непокрытой взносами задолженности W = D - Q. Отсюда размер взносов в последнем периоде
Ссуда с льготным периодом. На этом видеипотеки, вероятно, нет нужды останавливаться подробно. В льготном периоде здесь выплачиваются только проценты, поэтому основная сумма долга не изменяется. Расчет размеров взносов осуществляется так же, как и для стандартной ипотеки.
Ссуда с залоговым счетом. Как уже отмечалось выше, для должника в отношении метода погашения эта ипотека обычно не отличается от ипотечной схемы GPM. Для кредитора это стандартная ипотека. Такое совмещение двух схем достигается открытием специального залогового счета, на который должник (или третья сторона) вносит оговоренную сумму. С этого счета в погашение долга списываются некоторые суммы. Недостающие средства доплачиваются должником. Этим достигаются некоторое обеспечение выплат и сокращение расходов должника в первые т месяцев. Схема такой ипотеки представлена на рис. 8.3 (данные взяты из примера 8.4). В зависимости от того, какая величина задается, возможны различные постановки задачи. Рассмотрим одну из них — пусть заданным является размер залогового счета и необходимо определить суммы взносов с учетом частичного погашения путем списания с этого счета. Решение охватывает три этапа. На первом по формуле (8.1) рассчитывается необходимый размер взносов R, далее определяются суммы списания с залогового счета в первые m месяцев, на последнем этапе находятся суммы доплат до требуемого размера взносов R. Для определения сумм списания примем обозначения: Vt — сумма, списываемая с залогового счета; r — месячная ставка процента, начисляемого на средства залогового счета; Z — сумма залогового счета. Обычно суммы списания со счета сокращаются во временис постоянным темпом, таким образом, соответственно размеры доплат увеличиваются. Находим
Vt = Vt - 1 q = V 1 qt - 1 где q — годовой темп изменения сумм, списываемых с залогового счета. Суммы списаний представляют собой переменную ренту, современная стоимость которой равна первоначальной сумме залогового счета. Согласно формуле (5.15)
где V — дисконтный множитель по ставке r. Отсюда
В итоге Rt = R - Vt; t = 1,..., т. (8.11) Пример 8.4. Стоимость закладываемого имущества — 120 млн. руб. Продавец получает засчет ссуды 115 и от покупателя 5 млн. руб. Срок ипотеки — 10 лет. Покупатель открывает специальный счет (15 млн. руб.). На счет начисляются проценты по ставке 10% годовых номинальных(начисление помесячное), списание производится 20 месяцев, сумма списания уменьшается на 2% в месяц. Таким образом, Z = 15, т = 20, N = 120, q = 1,02, i = 12%, r = 10% (обе ставки годовые, номинальные). Находим R = 115000 /a 120;1 = 1649,92 тыс. руб.; Vi = 15000 Vt = 978,15 х 0,98 t - 1 Таким образом, суммы списания со счета равны: 978,15; 958,59;...; 653,33, а взносыдолжника в этом периоде 671,77; 691,33;...; 996,59.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.198.21 (0.046 с.) |

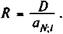 (8.1)
(8.1) (8.2)
(8.2)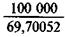 = 1434,709 тыс. руб.
= 1434,709 тыс. руб.
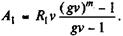 (8.7)
(8.7)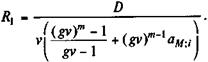 (8.9)
(8.9) = 1,004074.
= 1,004074.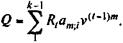
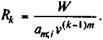

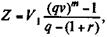
 (8.10)
(8.10)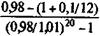 = 978,15 тыс. руб.;
= 978,15 тыс. руб.;


