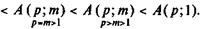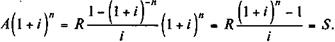Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Современная стоимость постоянной ренты постнумерандоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Годовая рента. Напомним, что под современной стоимостью потока платежей понимают сумму дисконтированных членов этого потока на некоторый предшествующий момент времени. Вместо терминов "современная стоимость" и "современная величина" потока платежей в зависимости от контекста употребляют термины капитализированная стоимость и приведенная величина. Как было показано выше, современная стоимость потока платежей эквивалентна в финансовом смысле всем платежам, которые охватывает поток. В связи с этим данный показатель находит широкое применение в разнообразных финансовых расчетах (планирование погашения долгосрочных займов, реструктурирование долга, оценка и сравнение эффективности производственных инвестиций и т. д.). В общем виде метод определения современной величины потока платежей (метод прямого счета) рассмотрен в параграфе 4.1. Здесь же объектом анализа является постоянная финансовая рента. Методы расчета современных стоимостей финансовых рент обсудим в том же порядке, что и методы наращения рент, и почти столь же детально. Начнем с самого простого случая — годовой ренты постнумерандо, член которой равен R,срок ренты n; ежегодное дисконтирование. Рента немедленная. В этих условиях дисконтированная величина первого платежа равна Rv, второго — Rv 2, последнего — Rvn. Как видим, эти величины образуют ряд, следующий геометрической прогрессии, с первым членом Rv и знаменателем v. Обозначим сумму членов этой прогрессии как А. Найдем ее:
Назовем множитель, на который умножается R, коэффициентом приведения ренты, обозначим его как an ; i. Этот коэффициент характеризует современную стоимость ренты с членом, равным 1. Чем выше значение i, тем меньше величина коэффициента. При увеличении срока ренты величина an ; i стремится к некоторому пределу. При п =
Полученное выражение применяется при расчете современной стоимости вечной ренты. Об этом речь пойдет в параграфе 4.5. График зависимости an ; i от n показан на рис 4.2. Значения an ; i табулированы. Фрагмент таблицы коэффициентов приведен в Приложении, табл. 5.
Пример 4.8. Рента постнумерандо характеризуется следующими параметрами: R = 4 млн. руб., п = 5. При дисконтировании по сложной ставке процента, равной 18,5% годовых, получим: A = 4 х a 5;18,5 = 4 Таким образом, все будущие платежи оцениваются в настоящий момент в сумме 12,368 млн. руб. Иначе говоря, 12,368 млн. руб., размещенных под 18,5% годовых, обеспечивают ежегодную выплату по 4 млн. руб. в течение пяти лет. Заметим, что формула (4.14) применяется и для определения современной стоимости p -срочной ренты. В этом случае переменная п означает число периодов, а i — ставку за период (но не годовую ставку). Годовая рента, начисление процентов m раз в году. Не будем выводить формулу для этого случая, а заменим в формуле (4.14) дисконтный множитель (1 + i)- n на эквивалентную величину (1 + j / m)- mn, соответственно i заменим на (1 + j/m) m - 1, после чего имеем:
Рента p -срочная (m = 1). Если платежи производятся не один, a p раз в году, то коэффициенты приведения находятся так же, как и в случае годовой ренты. Только теперь размер платежа равен R / p, а число членов np. Сумма дисконтированных платежей равна:
Пример 4.9. В гл. 1 (параграф 1.1) упоминалась авария на химическом заводе в Бхопале (Индия). Корпорация "Юнион кар-байд" первоначально предложила в качестве компенсации пострадавшим 200 млн. долл., выплачиваемых в течение 35 лет. Предложение было отклонено (За рубежом. 1985. № 11). Выше было отмечено, что такая компенсация адекватна 57,6 млн. долл., выплаченных единовременно. Покажем, как была рассчитана эта сумма. Если выплаты производятся помесячно на протяжении 35 лет равными суммами, то данный ряд платежей представляет собой постоянную ренту (p = 12) с годовой суммой выплат 200/35 = = 5,714 млн. долл. в год. Допустим, это рента постнумерандо. Тогда согласно формуле (4.17), положив i = 10%, получим: A = 5,714 Иначе говоря, капитал в сумме 57,59 млн. долл. при начислении 10% годовых был бы достаточен для выполнения обязательства. Рента p -срочная (p = m). Число членов ренты здесь равно числу начислений процентов; величина члена ренты составляет R / m. В итоге
Искомый результатможно получить и по формуле (4.14) и при этом воспользоватьсятаблицей коэффициентов приведения постоянныхрент. В этом случае вместочисла лет беретсяколичество периодов ренты, процентнаяставка и величиначлена ренты определяются соответствующим образом (см. пример 4.5). Рента p -срочная (p <> m). Сумма членов соответствующейпрогрессии составит
Ренты с непрерывным начислением процентов. Пусть, как и выше, ряд состоит из ежегодных платежей, равных R, однако проценты начисляются непрерывно, сила роста равна
Если имеет место p -срочная рента, то
Пример 4.10. Для условий примера 4.8 при Сравнение современных постоянных стоимостей рент постнумерандо с разными условиями. Как следует из приведенных примеров, величина современной стоимости заметно зависит от условий наращения процентов (точнее, дисконтирования) и частоты выплат в пределах года. Ниже приводятся соотношения современных стоимостей соответствующих рент. Современные стоимости обозначены как A (p; m), причем (1;1) — годовая рента с ежегодным начислением процентов, (p; Для одних и тех же годовых сумм выплат и процентных ставок (i =^ j =
Из приведенных неравенств следует, что рента с условиями p = 2 и m = 4 имеет меньшую современную стоимость, чем рента с p = 4 и m =2. Зависимость между наращенной и современной стоимостью постоянной ренты. В параграфе 4.1 показана зависимость между A и S y произвольного потока платежей — см. формулу (4.3). Для годовых и p -срочных постоянных рент постнумерандо с ежегодным начислением процентов находим:
Аналогичным образом получим: Svn = A. Для рент с начислением процентов m раз в году имеем: A (i + j / m) mn = S; (4.22) S (i+ j / m)- mn = A. (4.23) Нетрудно догадаться, что в аналогичной зависимости находятся и соответствующие коэффициенты. В частности: an;i (1 + i) n = sn;i; sn;ivn = an;i. Пример 4.11. Найдем современную стоимость для варианта ренты p = m = 4, взяв за основу S = 31,785 (см. пример 4.5). По формуле (4.23) получим: A = 31,785(1 + 0,185/4)-20 = 12,868 млн. руб.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 977; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.032 с.) |

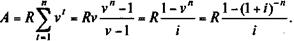 (4.14)
(4.14)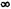 предельное значение коэффициента составит
предельное значение коэффициента составит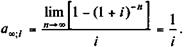 (4.15)
(4.15)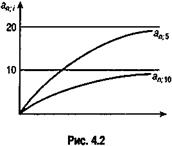
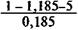 = 4 x 3,092 = 12,368 млн. руб.
= 4 x 3,092 = 12,368 млн. руб.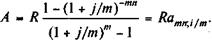 (4.16)
(4.16)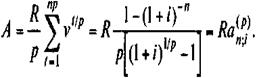 (4.17)
(4.17)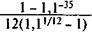 = 57,59 млн. долл.
= 57,59 млн. долл.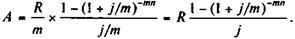 (4.18)
(4.18)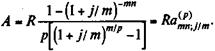 (4.19)
(4.19)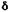 . При дисконтировании по этой ставке всех членов ряда получим геометрическую про-грессию с первым членом R и знаменателем
. При дисконтировании по этой ставке всех членов ряда получим геометрическую про-грессию с первым членом R и знаменателем 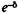 . Сумма членов про-грессии составит:
. Сумма членов про-грессии составит: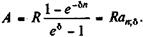 (4.20)
(4.20)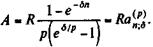 (4.21)
(4.21)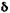 = 0,185 находим A = 4
= 0,185 находим A = 4 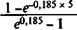 =11,878 млн. руб.
=11,878 млн. руб.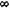 ) — p -срочная рента с непрерывным начислением процентов.
) — p -срочная рента с непрерывным начислением процентов.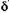 ) получим следующие неравенства:
) получим следующие неравенства: