Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резонансные явления в цепях синусоидального токаСодержание книги
Поиск на нашем сайте
Резонансными режимами в цепях синусоидального тока называются такие режимы, при которых сдвиг фаз φ между напряжением на участке цепи и током равен нулю. В цепи с последовательным соединением элементов R, L, C (рис. 2.26) сдвиг фаз между напряжением на зажимах участка цепи и током определяется через сопротивления этого участка цепи:
При равенстве реактивных сопротивлений Из условия возникновения резонансного режима 1) f=var, L=const, C=const; 2) f=const, L= var, C=const; 3) f=const, L=const, C= var. Характеристики, показывающие изменение напряжений, токов и других величин при изменении одного из параметров, называются резонансными характеристиками. Рассмотрим резонансные кривые тока I(ω), напряжений на индуктивности и емкости UL(ω) и UC(ω) и угла сдвига фаз φ(ω) (рис. 2.27). Ток в цепи При значении частоты ω=0 емкостное сопротивление ХС равно бесконечности и ток в цепи равен нулю. Далее с увеличением частоты емкостное сопротивление уменьшается, а индуктивное увеличивается и ток возрастает до максимального значения при резонансе Ip=U/R. При дальнейшем увеличении частоты ток уменьшается и при ω→∞, когда индуктивное сопротивление стремится к бесконечности, он стремится к нулю. напряжение на индуктивности определяется
В резонансной цепи комплексное сопротивление равно активному сопротивлению и имеет минимальное значение Z=R=min. Ток в такой цепи, как было показано выше, будет иметь максимальное значение: IР =U/Z=U/R= Imax. В случае если реактивные сопротивления по величине гораздо больше активного сопротивления
Соотношение напряжений в резонансном режиме определяется величиной добротности Q контура, величина которой определяется исходя из следующих соображений:
где Q – добротность цепи, состоящей из последовательно соединенных элементов R, L, C, значение которой может достигать десятков и сотен единиц. При изменении частоты от 0 до ωр угол сдвига фаз φ между напряжением и током изменяется от (-π/2) до 0. При изменении частоты ω до ∞ угол φ возрастает от 0 до π/2. При параллельном соединении элементов R, L, C в цепи (рис. 2.28) наблюдается резонанс токов. Угол сдвига фаз между входным напряжением и током в цепи при параллельном соединении приемников определяется
Резонансные характеристики для режима резонанса токов построены на рис. 2.29. Входной ток цепи определяется согласно первому закону Кирхгофа: Ток резистора от частоты питающего напряжения не зависит и будет всегда неизменным. При частоте равной нулю конденсатор представляет
собой разомкнутый участок цепи и его ток равен нулю, а ток идеальной катушки стремится к бесконечности, так как катушки представляет собой короткозамкнутый участок. Входной ток при этом равен току катушки и стремится к бесконечности. При резонансной частоте ωрез действующие значения емкостного и индуктивного токов равны. Эти токи находятся в противофазе и их векторная сумма равна нулю, входной ток равен току активного элемента и имеет минимальное значение. При частоте стремящейся к бесконечности проводимость емкостного элемента стремится к бесконечности, а проводимость индуктивного элемента - к нулю. Входной ток становится практически равным току конденсатора и также стремится к бесконечности. При частотах меньше резонансной ω<ωрез угол сдвига фаз больше нуля φ>0, преобладает индуктивная составляющая проводимости. При частоте равной резонансной ω=ωрез реактивные составляющие проводимостей равны и угол сдвига фаз равен нулю φ=0. При частотах больше резонансной ω>ωрез угол сдвига фаз меньше нуля φ<0 и стремится к значению -π/2, преобладает емкостная составляющая проводимости.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.103.33 (0.008 с.) |


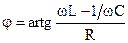 .
. он становится равным нулю. Напряжения на индуктивном и емкостном элементах равны между собой, поэтому резонанс в рассматриваемой цепи называют резонансом напряжений. Входное напряжение при этом равно напряжению на активном сопротивлении.
он становится равным нулю. Напряжения на индуктивном и емкостном элементах равны между собой, поэтому резонанс в рассматриваемой цепи называют резонансом напряжений. Входное напряжение при этом равно напряжению на активном сопротивлении. следует способ его достижения. Резонанс напряжений в цепи можно получить путем изменения одной из трех величин при постоянстве двух других:
следует способ его достижения. Резонанс напряжений в цепи можно получить путем изменения одной из трех величин при постоянстве двух других:
 и своей формой напоминает кривую зависимости тока I(ω).
и своей формой напоминает кривую зависимости тока I(ω).
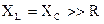 , в режиме резонанса напряжения на индуктивности и емкости могут во много раз превышать входное напряжение:
, в режиме резонанса напряжения на индуктивности и емкости могут во много раз превышать входное напряжение:
 .
. ,
, .
. При равенстве реактивных составляющих проводимостей:
При равенстве реактивных составляющих проводимостей:  или
или 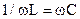 угол сдвига фаз будет равен нулю, что и будет являться условием резонанса токов, при котором, равны реактивные составляющие токов индуктивного и емкостного элементов, входной ток равен току активного элемента и имеет минимальное значение.
угол сдвига фаз будет равен нулю, что и будет являться условием резонанса токов, при котором, равны реактивные составляющие токов индуктивного и емкостного элементов, входной ток равен току активного элемента и имеет минимальное значение.