
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Активная, реактивная, полная мощности.Содержание книги
Поиск на нашем сайте
Треугольник мощностей. Коэффициент мощности
Если все стороны треугольника сопротивлений (рис. 2.14) домножить на величину I2, то на комплексной плоскости получим треугольник, подобный треугольнику сопротивлений, все стороны которого пропорциональны мощностям:
jQL=jXLI2 – реактивная индуктивная мощность; -jQC=-jXCI2 – реактивная емкостная мощность;
Треугольник (рис. 2.15), полученный на комплексной плоскости, называют треугольником мощностей.
Комплексная мощность также может быть записана, как
где
Комплексная мощность может быть также рассчитана по формуле если Коэффициентом мощности цепи называют косинус угла сдвига фаз, то есть отношение активной мощности к полной
Параллельное соединение элементов R, L, C
На вход электрической цепи (рис. 2.16), состоящей из соединенных параллельно элементов R, L, C подано синусоидальное напряжение u(t)=Umsin(ωt+ψu). Запишем уравнение по первому закону Кирхгофа для мгновенных значений токов цепи:
Сумме синусоидальных токов соответствует сумма изображающих их комплексных величин, тогда для действующих комплексных значений можно записать:
Величину
Необходимо заметить, что в том случае если ветвь содержит и активные и реактивные элементы, то активная и реактивная составляющие полной проводимости такой ветви будут определяться по формулам:
Запишем комплексную проводимость в показательной форме:
где
Комплексный ток можно записать:
где
Построим векторную диаграмму токов и напряжения на зажимах цепи (рис. 2.17), приняв начальную фазу напряжения за ноль. Ток активного элемента совпадает по фазе с напряжением, поэтому на векторной диаграмме вектор этого тока изображается параллельно вектору напряжения. Ток индуктивного элемента отстает от напряжения на угол 90 градусов, поэтому на векторной диаграмме индуктивный ток повернут относительно вектора напряжения на 90 градусов по направлению движения часовой стрелки. Ток емкостного элемента опережает напряжение на угол 90 градусов, поэтому емкостный
ток повернут относительно вектора напряжения против направления часовой стрелки на 90 градусов. Необходимо отметить, что токи индуктивного и емкостного элементов находятся в противофазе, вследствие чего в цепи переменного тока при параллельном соединении этих элементов могут создаваться условия, невозможные для цепей постоянного тока, когда токи отдельных элементов будут значительно превышать входной ток. Треугольник, образованный векторами токов, принято называть треугольником токов. Если каждую сторону треугольника токов поделить на величину действующего комплексного напряжения, то получим треугольник (рис. 2.18), подобный исходному и называемый треугольником проводимостей. Как видно из полученных векторных диаграмм (рис. 2.17 и 2.18), угол сдвига фаз зависит от соотношения параметров цепи: при
при Анализ цепей при смешанном соединении приемников. Комплексный метод расчета Для расчета цепей синусоидального тока используется комплексный метод расчета. Он основан на изображении синусоидальных функций времени комплексными числами. Соответственно дифференциальные и интегральные зависимости между напряжениями и токами в цепях синусоидального тока, заменяются линейными зависимостями между комплексными токами и напряжениями:
Рассмотрим определение всех токов и напряжений в схеме, показанной на рис.2.19, питающейся от источника синусоидального напряжения, комплексное действующее значение которого Параметры элементов цепи: R1=50 Ом; R2=XL=XC =100 Ом. Расчет будем выполнять, применяя эквивалентные преобразования в электрических цепях и закон Ома. Определим комплексные сопротивления ветвей:
Для того чтобы по закону Ома определить ток на входе цепи, необходимо рассчитать комплексное сопротивление цепи относительно входных зажимов. Сопротивления второй и третьей ветвей соединены параллельно, поэтому их эквивалентное сопротивление относительно зажимов 2-4 можно рассчитать:
Относительно входных зажимов сопротивление первой ветви и сопротивление Z23 соединены последовательно, поэтому входное сопротивление всей цепи можно определить как сумму комплексных сопротивлений:
Входной ток
Напряжение на зажимах параллельных ветвей:
Зная напряжения параллельных ветвей, можно определить по закону Ома токи
Определим напряжения на участках цепи:
Построим векторную диаграмму токов и напряжений цепи. Для этого на комплексной плоскости в соответствующих масштабах тока mi и напряжения mu построим векторы рассчитанных напряжений и токов со своими начальными фазами (рис. 2.20). На векторной диаграмме хорошо видно выполнение законов Кирхгофа:
2.10. Топографическая диаграмма
Отличительная особенность этих диаграмм состоит в том, что векторы напряжений на зажимах элементов сложной цепи на топографической диаграмме располагают в том порядке, в котором расположены соответствующие элементы цепи. При этом вектор напряжения на последующем элементе цепи обязательно примыкает к вектору напряжения на предыдущем элементе, в то время как на обычных векторных диаграммах любой вектор можно переносить параллельно самому себе в любое место комплексной плоскости.
Отложим вектор тока
точка, соответствующая концу этого вектора. Аналогично рассчитываем и наносим на комплексную плоскость потенциалы остальных точек схемы:
Для определения напряжения между двумя любыми точками схемы достаточно соединить соответствующие точки топографической диаграммы отрезком прямой и придать этому вектору надлежащее направление. Так, вектор напряжения Топографическую диаграмму практически всегда строят в одних осях координат с векторной диаграммой токов. Заметим, что при выборе обхода ветвей схемы навстречу положительному направлению тока топографическая диаграмма совпадает с понятием векторной диаграммы. То есть ее можно строить, употребляя привычные нам знания: напряжение на резисторе совпадает по фазе с током, напряжение на индуктивном элементе опережает ток на угол 90º, а на емкостном элементе напряжение отстает от тока на угол 90º. При выборе обхода схемы по току все векторы изменяют свое направление на 180º.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 613; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.11.247 (0.009 с.) |

 , [Вт]- активная мощность;
, [Вт]- активная мощность; , [ВАр] - реактивная мощность;
, [ВАр] - реактивная мощность; ,[ВА] - комплексная мощность.
,[ВА] - комплексная мощность.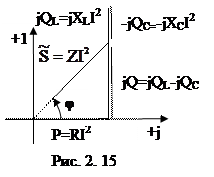
 ,
, – полная мощность, модуль комплексной мощности;
– полная мощность, модуль комплексной мощности; - угол сдвига фаз между напряжением и током в цепи.
- угол сдвига фаз между напряжением и током в цепи. , где
, где  комплексно-сопряженный ток;
комплексно-сопряженный ток; , то
, то 
 .
.

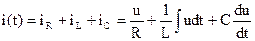 .
.
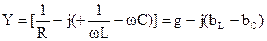 - называют комплексной проводимостью цепи с параллельным соединением элементов R, L, C, которая определяется как сумма проводимостей параллельных ветвей;
- называют комплексной проводимостью цепи с параллельным соединением элементов R, L, C, которая определяется как сумма проводимостей параллельных ветвей; активная составляющая проводимости;
активная составляющая проводимости; - реактивная индуктивная составляющая проводимости;
- реактивная индуктивная составляющая проводимости; - реактивная емкостная составляющая проводимости.
- реактивная емкостная составляющая проводимости. ,
,  .
. ,
,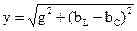 - полная проводимость, модуль комплексной проводимости;
- полная проводимость, модуль комплексной проводимости; - угол сдвига фаз между напряжением на зажимах цепи и входным током, который определяется соотношением активной и реактивной проводимостей.
- угол сдвига фаз между напряжением на зажимах цепи и входным током, который определяется соотношением активной и реактивной проводимостей. ,
, - действующее значение входного тока;
- действующее значение входного тока; - начальная фаза тока;
- начальная фаза тока;
 угол φ>0, ток отстает по фазе от напряжения;
угол φ>0, ток отстает по фазе от напряжения; при
при  угол φ<0, ток опережает по фазе напряжение;
угол φ<0, ток опережает по фазе напряжение; угол φ=0, ток совпадает по фазе с напряжением и цепь ведет себя как чисто активное сопротивление; такой режим работы цепи называется режимом резонанса токов.
угол φ=0, ток совпадает по фазе с напряжением и цепь ведет себя как чисто активное сопротивление; такой режим работы цепи называется режимом резонанса токов. →
→ 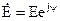
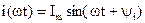 →
→  →
→ 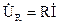
 →
→ 
 →
→ 
 Далее расчеты в цепях синусоидального тока выполняются теми же методами, что и расчеты в цепях постоянного тока (метод эквивалентных преобразований, законов Кирхгофа, контурных токов, узловых потенциалов и т.д.), только все сопротивления, токи и напряжения записываются в комплексной форме записи.
Далее расчеты в цепях синусоидального тока выполняются теми же методами, что и расчеты в цепях постоянного тока (метод эквивалентных преобразований, законов Кирхгофа, контурных токов, узловых потенциалов и т.д.), только все сопротивления, токи и напряжения записываются в комплексной форме записи.
 Ом;
Ом;  Ом;
Ом;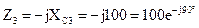 Ом.
Ом.


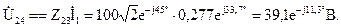



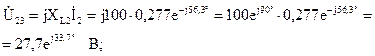


 ,
,
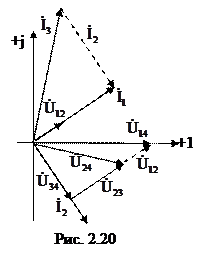


 в произвольно выбранном направлении (рис. 2.22). Примем потенциал точки g равным нулю (
в произвольно выбранном направлении (рис. 2.22). Примем потенциал точки g равным нулю ( ) и определим потенциалы остальных точек схемы относительно этого потенциала. Обход схемы при построении топографической диаграммы выберем навстречу току. Тогда потенциал точки f будет больше потенциала точки g на величину напряжения на резисторе R1:
) и определим потенциалы остальных точек схемы относительно этого потенциала. Обход схемы при построении топографической диаграммы выберем навстречу току. Тогда потенциал точки f будет больше потенциала точки g на величину напряжения на резисторе R1:  . Наносим вектор
. Наносим вектор  на комплексную плоскость и конец этого вектора обозначаем буквой f. Причем сам вектор комплексного потенциала не изображается на плоскости, а показывается только
на комплексную плоскость и конец этого вектора обозначаем буквой f. Причем сам вектор комплексного потенциала не изображается на плоскости, а показывается только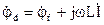 ;
;  ;
;  .
.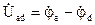 представлен на топографической диаграмме отрезком прямой, соединяющим точки а и d, соответствующие концам векторов комплексных потенциалов
представлен на топографической диаграмме отрезком прямой, соединяющим точки а и d, соответствующие концам векторов комплексных потенциалов  и
и  . Этот вектор направлен от точки d к точке а, что соответствует правилу вычитания векторов.
. Этот вектор направлен от точки d к точке а, что соответствует правилу вычитания векторов.


