Резонанс напряжений и резонанс токов.

Резонанс напряжений. В цепи переменного тока, с последовательно включенными L, C и R, полное сопротивление контура имеет минимальное значение Z_min = R, если ωL = 1/ωC. В этом случае ток в цепи определяется этим сопротивлением, принимая максимальные значения (возможные при данном U_m), что свидетельствует о наличии резонансной частоты ω_рез для тока, значение которой определяется по условию ωL = 1/ωC, откуда ω_рез = 1/√LC = ω₀

т.е. резонансная частота для силы тока равна частоте собственных колебаний в контуре. Напряжение на R равно внешнему напряжению, приложенному к цепи (U_R =U).

Это явление называется резонансом напряжений (последовательным резонансом) – резкое возрастание амплитуды силы тока в контуре с последовательно включенными L, C, R и Е при

ω_рез = 1/√LC = ω₀. В случае резонанса напряжений (U_L)_рез = (U_С)_рез.

Подставив в эту формулу значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе получим (U_L)_рез = (U_С)_рез = I_m √L/C = (U_m/R)√L/C = QU_m,

где Q – добротность контура. Добротность контура определяет остроту резонансных кривых. Так как Q обычных колебательных контуров больше единицы, то (U_L)_рез = (U_С)_рез > Е, т.е. добротность показывает, во сколько раз напряжение на конденсаторе (катушке) больше напряжения приложенного к цепи.

Е = E₀ cos ω_резt, I_рез = (E₀ /R)cos ω_резt, I₀^max = E₀ /R.

Резонанс токов. Рассмотрим цепь переменного тока, содержащую параллельно включенные L и С, R = 0.

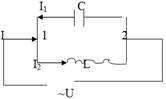
Если приложенное напряжение изменяется по закону U =U_mcosωt, то в ветви 1С2 течет ток I₁ = I_m1cos(ωt–φ₁), φ₁ = (2n+3/2)π, n=1, 2, 3,... амплитуда которого при условии L = 0 и R = 0: I_m1 = U_m/(1/ωC).

Аналогично, сила тока в цепи 1L2 I₂ = I_m2cos(ωt–φ₂), φ₂ = (2n+1/2)π, n=1, 2, 3,... амплитуда которого при условии R = 0 и С=∞ (условие отсутствия емкости в цепи): I_m2 = U_m/(ωL).

Cравнив видим, что φ₂ - φ₁ =π, т.е. токи в ветвях противоположны по фазе. Амплитуда тока во внешней (неразветвленной) цепи I_m = | I_m1 - I_m2 |= U_m|ωC – 1/(ωL)|. Если ω = ω_рез = 1/√(LС), то I_m1 = I_m2 и I_m = 0.

Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты ω приложенного напряжения к резонансной частоте ω_рез называется резонансом токов (параллельным резонансом).

Амплитуда тока оказалась равной нулю, так как считали, что активное сопротивление контура R = 0. При R ≠ 0 разность фаз φ₂ - φ₁ ≠ π, поэтому I_m ≠ 0 и сила тока I в подводящих проводах примет наименьшее возможное значение, обусловленное только током через резистор. При резонансе токов силы токов I₁ и I₂ могут значительно превышать силу тока I.Рассмотренный контур оказывает большое сопротивление переменному току с частотой, близкой к резонансной. Поэтому его свойства используются в резонансных усилителях, позволяющих выделить одно определенное колебание из сигнала сложной формы.

7. Общая характеристика теории Максвелла. Уравнения Максвелла. Вихревое магнитное поле??? Ток смещения. (все интегралы круговые!!!)

Первое уравнение Максвелла в интегральной форме. Согласно определению, э.д.с. равна циркуляции вектора напряженности электрического поля Е:

 

Е = ∫ E· d l, (2)

^L

которая для потенциального поля равна нулю. В общем случае изменяющегося вихревого поля для Е_ин получим

 

∫ E· d l = - dФ_m /dt = -∫(∂ B /∂t)d S. (3)

^{L S}

(3) – первое уравнение Максвелла: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру L равна взятой с обратным знаком скорости изменения потока вектора магнитной индукции через поверхность, ограниченную данным контуром. Знак «- «соответствует правилу Ленца для направления индукционного тока. Отсюда следует, что переменное магнитное поле создает в пространстве вихревое электрическое поле независимо от того, находится в этом поле проводник (замкнутый проводящий контур) или нет. Полученное таким образом уравнение (3) является обобщением уравнения (2), которое справедливо только для потенциального поля, т.е. электростатического поля.

Ток смещения и второе уравнение Максвелла в интегральной форме. Максвелл высказал гипотезу, что магнитное поле порождается не только электрическими токами, текущими в проводнике, но и переменными электрическими полями в диэлектриках или вакууме.

Ток проводимости вблизи обкладок конденсатора можно записать так

I = dq/dt = (d/dt)∫σ dS = ∫(∂σ/∂t)dS = ∫(∂D/∂t)dS

^{S S S}

(поверхностная плотность заряда σ на обкладках конденсатора равна электрическому смещению D в конденсаторе).

Подынтегральное выражение можно рассматривать как частный случай скалярного произведения (∂ D /∂t)dS, когда (∂ D /∂t) и d S взаимно параллельны. Поэтому для общего случая можно записать I = ∫(∂ D /∂t)dS j _см = ∂ D/ ∂t. (5) Выражение(5) Максвелл назвал плотностью тока смещения. Направление вектора плотности тока j и j _см совпадает с направлением вектора ∂ D /∂t.

второе уравнение Максвелла: циркуляция вектора напряженности Н магнитного поля по любому замкнутому контуру L равна суммарному току проводимости, который пронизывает поверхность S, натянутую на этот контур, сложенному со скоростью изменения потока вектора электрической индукции D через эту поверхность.

Третье и четвертое уравнения Максвелла. Третье уравнение Максвелла выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только электрическими токами), т.е. теорема Гаусса оказалась справедливой не только для электро- и магнитостатических полей, но и для переменного во времени вихревого электромагнитного поля:

 

∫ D d S = q,

^S

∫ B d S = 0.

^S