
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сопротивление контура при резонансеСодержание книги
Поиск на нашем сайте
В этом случае ток I в неразветвленной части цепи совпадает по фазе с входным напряжением U (рис. 1.9, b). При резонансе наблюдается резкое увеличение токов IL и IC в параллельных ветвях контура, в то время, как общий ток I в неразветвленной части цепи остается незначительным. Поэтому параллельный резонанс называется резонансом токов. При резонансе ток I в неразветвленной части контура равен: I =
где U – напряжение на входе контура; Rое – эквивалентное сопротивление параллельного колебательного контура при резонансе. Резонансный ток I кв контуре, образованном параллельными ветвями, протекает одновременно как через индуктивность, так и через емкость:
Токи в индуктивной и емкостной ветвях:
Мощность, подводимая к контуру, равна мощности, выделяемой на активном сопротивлении контура:
Разделив обе части уравнения на U 2, получаем:
Тогда эквивалентное сопротивление контура при резонансе можно выразить следующим образом:
Выразим Rое через добротность контура:
Таким образом, эквивалентное сопротивление Rое параллельного колебательного контура при резонансе в Q раз больше, чем реактивное сопротивление каждой из ветвей контура. Практически величина Rое составляет несколько десятков кОм.
Полоса пропускания
Любой колебательный контур обладает свойством избирательности. Чем меньше разность Δ f между частотой f источника сигнала и резонансной частотой f 0 контура, тем больший ток создает в контуре этот источник.
На рис. 3.1.10 показаны границы относительной полосы пропускания двух контуров, имеющих разную добротность.
Рис. 3.1.10. Обобщенные резонансные кривые колебательных контуров
СОБСТВЕННЫЕ КОЛЕБАНИЯ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Ранее рассматривалась работа колебательных контуров, в которых потери энергии восполняются за счет энергии внешнего источника. Такой режим работы называется режимом вынужденных колебаний.
Рис. 1.1.11. Схема для исследования процесса установления собственных колебаний в контуре
Если подвижный контакт переключателя находится в положении “1”, то конденсатор С заряжен до напряжения Um, равного напряжению источника питания Е. При переводе подвижного контакта переключателя из положения “1” в положение “2” начинается разряд конденсатора С через катушку индуктивности L и резистор R. В результате противодействия ЭДС самоиндукции, возникающей в катушке индуктивности, ток разряда конденсатора будет нарастать постепенно. В начале разряда скорость нарастания тока максимальна, а по мере разряда конденсатора скорость нарастания тока уменьшается. Нарастание тока прекратится в тот момент, когда напряжение на конденсаторе уменьшится до нуля. В этот момент величина тока будет максимальной. К указанному моменту вся энергия, запасенная в конденсаторе, будет израсходована. Часть этой энергии окажется израсходованной на нагрев резистора R, а оставшаяся часть перешла в энергию, запасенную в магнитном поле катушки индуктивности. Однако, несмотря на то, что напряжение на конденсаторе, вызвавшее появление тока в цепи, стало равным нулю, протекание тока в цепи сразу не прекращается, т. к. действует ЭДС самоиндукции. Ток будет протекать в прежнем направлении, перезаряжая конденсатор. При этом напряжение на конденсаторе начинает возрастать, а ток в катушке начинает уменьшаться. Когда вся энергия магнитного поля катушки, за исключением потерь, перейдет в энергию электрического поля конденсатора, ток в катушке уменьшится до нуля, и возрастание напряжения на конденсаторе прекратится. К этому моменту напряжение на конденсаторе достигнет максимального значения. Далее процесс повторяется с той разницей, что энергия, запасенная в электрическом поле конденсатора, уменьшилась за счет потерь на сопротивлении R. Описанный обмен энергией будет происходить до тех пор, пока вся энергия, запасенная в конденсаторе при его заряде от источника питания, будет израсходована на сопротивлении потерь контура. Такие колебания называются затухающими колебаниями. Амплитуда затухающих колебаний уменьшается по экспоненциальному закону:
Интенсивность затухания колебаний определяется добротности контура.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 141; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.115.79 (0.011 с.) |

 Резонанс в параллельном колебательном контуре наблюдается при равенстве реактивных сопротивлений индуктивной и емкостной ветвей:
Резонанс в параллельном колебательном контуре наблюдается при равенстве реактивных сопротивлений индуктивной и емкостной ветвей: ;
;
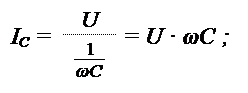


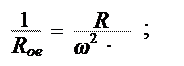
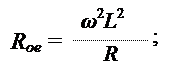


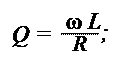

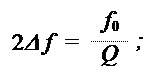 Полоса частот 2Δ f, в пределах которой ток в контуре превышает уровень, составляющий 1/
Полоса частот 2Δ f, в пределах которой ток в контуре превышает уровень, составляющий 1/  » 0,7 от максимального, называется полосой пропускания контура. Ширина полосы пропускания контура зависит от его резонансной частоты и добротности:
» 0,7 от максимального, называется полосой пропускания контура. Ширина полосы пропускания контура зависит от его резонансной частоты и добротности:
 Режим работы контура без пополнения энергии называется режимом собственных колебаний. Схема колебательного контура, работающего в режиме собственных колебаний, приведена на рис. 3.1.11.
Режим работы контура без пополнения энергии называется режимом собственных колебаний. Схема колебательного контура, работающего в режиме собственных колебаний, приведена на рис. 3.1.11.
 Если добротность контура Q ≤ 0,5, то колебания в контуре полностью затухают в течение первого полупериода. Такой разряд конденсатора называется неколебательным или апериодическим (рис. 3.1.12, b).
Если добротность контура Q ≤ 0,5, то колебания в контуре полностью затухают в течение первого полупериода. Такой разряд конденсатора называется неколебательным или апериодическим (рис. 3.1.12, b).



