
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Емкость в цепи переменного токаСодержание книги
Поиск на нашем сайте
При включении конденсатора в цепь переменного тока происходит периодический заряд и разряд конденсатора С. При питании переменным током величина напряжения изменяется во времени по синусоидальному закону:
Величина заряда q конденсатора, имеющего емкость С, в любой момент времени t равна произведению его емкости на мгновенное значение напряжения:
Поэтому величина заряда конденсатора изменяется во времени тоже по синусоидальному закону:
Изменение напряжения на конденсаторе на величину du в течение малого промежутка времени dt приводит к изменению его заряда на величину dq:
dq = C · du
dq = w · C · Um · cos w t dt = w · C · Um · sin (w t + 90º) dt;
Величина тока заряда конденсатора определяется изменением заряда в единицу времени:
Тогда ток заряда равен:
Реактивное сопротивление xС конденсатора определяется величиной его емкости и частотой приложенного напряжения:
Амплитуда тока:
Тогда мгновенные значения тока заряда определяются следующим выражением:
Таким образом, в конденсаторе, включенном в цепь переменного тока, ток опережает приложенное напряжение на 90º.
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ ПОСЛЕДОВАТЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР Схема последовательного колебательного конура В схему последовательного колебательного контура входят конденсатор С, катушка индуктивности L и резистор R. Все эти элементы образуют одну непрерывную цепь, в которой протекает один и тот же ток I (рис. 3.1.5).
Рис. 3.1.5. Схема последовательного колебательного контура Конденсатор и катушка индуктивности способны накапливать энергию. Конденсатор запасает электрическую энергию, катушка индуктивности – магнитную Энергия, запасаемая конденсатором:
где С – емкость конденсатора; U – напряжение, приложенное к обкладкам конденсатора.
Энергия, накапливаемая катушкой индуктивности:
где L – индуктивность катушки; I – ток, протекающий через катушку. В большинстве случаев резистор R в виде отдельного элемента в контур не включается. Однако, катушка индуктивности, конденсатор и соединительные провода имеют активные потери, которые эквивалентны потерям на активном сопротивлении R.
Векторные диаграммы
Рис. 3.1.6. Векторные диаграммы последовательного колебательного контура
При построении векторной диаграммы напряжений за исходный вектор принят вектор тока I, т. к. значение тока в последовательном колебательном контуре одинаково для всех элементов цепи. Вектор напряжения на активном сопротивлении UR совпадает по фазе с вектором тока I. Вектор напряжения на конденсаторе отстает от вектора тока на 90º. Вектор напряжения на катушке индуктивности опережает вектор тока на 90º. Суммарное напряжение U на зажимах всей цепи равно геометрической сумме трех указанных напряжений. При построении диаграммы сопротивлений следует учесть, что во всей цепи протекает один и тот же ток I. Сопротивление каждого элемента цепи можно получить, разделив соответствующий вектор напряжения на величину тока I. Поэтому диаграмма сопротивлений отличается от диаграммы напряжений только величиной масштаба. Общее сопротивление последовательного колебательного контура равно геометрической сумме сопротивлений входящих в него элементов:
Отсюда видно, что сопротивление Z колебательного контура зависит от частоты w подводимого к нему напряжения. Угол сдвига фаз между напряжением U и током I:
Ток в контуре
Ток I в контуре определяется по следующей формуле:
I =
Ток в контуре будет наибольшим в том случае, когда величина сопротивления Z, зависящая от частоты w, будет минимальной: Z =
Общее сопротивление Z будет минимальным при такой частоте w0, при которой индуктивное сопротивление катушки окажется равным емкостному сопротивлению конденсатора:
Тогда Z =
Следовательно, колебательный контур ведет себя так же, как активное сопротивление. В этом случае Z = R и j = 0º.
Учитывая, что при резонансе можно найти значение резонансной частоты w 0:
w 0 =
Величина r = w 0 L = Характеристическое сопротивление представляет собой величину сопротивления каждого из реактивных элементов контура при резонансе. В этом случае значения сопротивлений указанных элементов равны по величине и противоположны по знаку. Выразив значение резонансной частоты через параметры реактивных элементов, получаем:
r = w 0 L =
Коэффициент Q =
Резонансная кривая
Практический интерес представляет отношение амплитуды тока в контуре при произвольной частоте к амплитуде тока при резонансной частоте w 0 : Ток в контуре при любой частоте:
Ток в контуре при резонансе:
Это уравнение называется уравнением резонансной кривой колебательного контура. Резонансная кривая полностью определяет свойства колебательного контура (рис. 3.1.7).
Рис. 3.1.7. Резонансная кривая колебательного контура
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 86; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.18.135 (0.01 с.) |


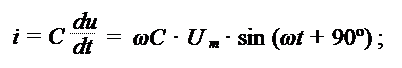
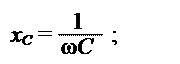

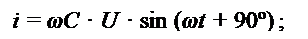
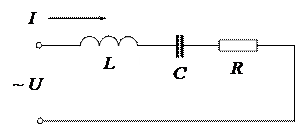
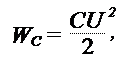
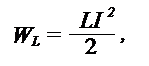
 Векторные диаграммы напряжений и сопротивлений последовательного колебательного контура выглядят следующим образом (рис. 3.1.6):
Векторные диаграммы напряжений и сопротивлений последовательного колебательного контура выглядят следующим образом (рис. 3.1.6):


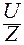 ;
;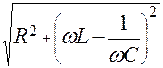 ;
;
 = R;
= R; Условие, при котором соблюдается это равенство, называется резонансом.
Условие, при котором соблюдается это равенство, называется резонансом. = 1;
= 1; ;
; называется характеристическим сопротивлением контура.
называется характеристическим сопротивлением контура. ;
; =
= 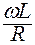 =
= 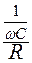 называется добротностью контура.
называется добротностью контура.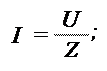

 Отношение тока при произвольной частоте к току при резонансе:
Отношение тока при произвольной частоте к току при резонансе:



