
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И основные нелинейные процессыСодержание книги
Поиск на нашем сайте
Нелинейные элементы и их характеристики
Элементы электрических цепей, в которых протекающий ток имеет нелинейную зависимость от приложенного напряжения, называются нелинейными элементами. К числу нелинейных элементов относятся электронные лампы, полупроводниковые приборы и т. п. Электрические цепи, содержащие нелинейные элементы, называются нелинейными цепями. Нелинейная зависимость протекающего тока от приложенного напряжения может быть аппроксимирована полиномом, степень которого зависит от требуемой точности ее аппроксимации: i = a 0 + a 1 · u + a 2 · u 2 + a 3 · u 3 + …. + an · un;
где a 0, a 1, a 2, a 3, …. a n – коэффициенты, не зависящие ни от u, ни от i. Допустим, зависимость тока, протекающего через нелинейный элемент, от напряжения, приложенного к этому элементу, описывается уравнением: i = a 2 · u 2;
Если на нелинейный элемент воздействует напряжение, являющееся суммой двух синусоидальных колебаний разных частот: u = U 1 m · sin ω1 t + U 2 m · sin ω2 t, то суммарный ток, протекающий через этот элемент, определяется следующим выражением: i = a 2 · (U 1 m · sin ω1 t + U 2 m · sin ω2 t)2;
Раскрывая скобки и используя простые тригонометрические преобразования, получаем:
i = + a 2 · U 1 m · U 2 m · [cos (ω1 – ω2) t – cos (ω1 + ω2) t ];
Результат, полученный после преобразования, содержит составляющие с частотами 2ω1, 2ω2, (ω1 – ω2), и (ω1 + ω2). Любую из этих частот можно выделить с помощью фильтров. Таким образом, с помощью нелинейных элементов можно производить преобразование частот
Глава 1. ПРЕОБРАЗОВАНИЕ СИГНАЛОВ И СПЕКТРОВ Модуляция
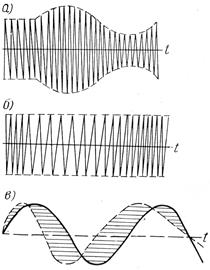
Для передачи низкочастотного сигнала с помощью высокочастотных синусоидальных колебаний необходимо, чтобы один из основных параметров высокочастотных колебаний изменялся под воздействием низкочастотного сигнала. Указанный процесс изменения параметров называется модуляцией. В зависимости от того, на какой параметр высокочастотных колебаний воздействует низкочастотный модулирующий сигнал, модуляция бывает амплитудной, частотной или фазовой (рис. 4.1.1).
а) амплитудная модуляция
б) частотная модуляция
в) фазовая модуляция
Рис. 4.1.1. Модулированные колебания
Амплитудная модуляция
Рис. 4.1.2. Амплитудно-модулированные колебания Воображаемая кривая, соединяющая точки, соответствующие амплитудным значениям высокой частоты, называется огибающей. При отсутствии модуляции амплитуда высокочастотных колебаний I 0 остается неизменной: I 0 = где I max и I min – максимальная и минимальная величины амплитуды высокочастотных колебаний.
При модуляции происходит изменение амплитуды высокочастотных колебаний Δ I в пределах от I min до I max:
Δ I = Отношение изменения амплитуды модулированных колебаний Δ I к амплитуде высокочастотных колебаний при отсутствии модуляции I 0 называется коэффициентом модуляции " m": m = Поскольку коэффициент модуляции всегда меньше единицы, то его обычно выражают в процентах.
|
|||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.250.15 (0.01 с.) |

 · (
· (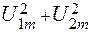 ) –
) – 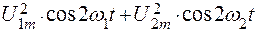 ) +
) +
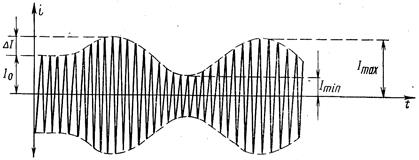 Высокочастотные колебания, амплитуда которых изменяется в соответствии с изменениями низкочастотного управляющего сигнала, называются амплитудно-модулированными колебаниями (рис. 4.1.2).
Высокочастотные колебания, амплитуда которых изменяется в соответствии с изменениями низкочастотного управляющего сигнала, называются амплитудно-модулированными колебаниями (рис. 4.1.2). ;
; ;
;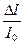 =
= 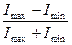 ;
;


