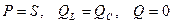Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резонансная частота, добротность последовательного контураСодержание книги
Поиск на нашем сайте
Выведем формулу резонансной частоты:
Вывод: резонанс напряжений наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура Настроить контур в резонанс можно: 1) изменяя L или C, при этом подгоняем частоту собственных колебаний под частоту питающего напряжения; 2) можно изменять частоту питания, подгоняя её под частоту собственных колебаний контура. Т. к. Сопротивление катушки и конденсатора на резонансной частоте равно характеристическому сопротивлению контура. Формула добротности:
Вывод: добротность в последовательном контуре показывает, во сколько раз напряжение на выходе больше, чем на входе в момент резонанса. Расстройка колебательного контура. Виды расстроек. Входные АЧХ и ФЧХ последовательного колебательного контура. Характер реактивного сопротивления последовательного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной Расстройка — отклонение частоты от резонансной. Различают: 1) Абсолютная расстройка — разность текущей частоты и резонансной:
Расстройка может и положительной и отрицательной. 2) Относительная расстройка — отношение абсолютной расстройки к резонансной частоте:
3) Обобщённая расстройка — отношение реактивного сопротивления x к резистивному:
Обычно входные характеристики строят от расстройки.
Входные АЧХ и ФЧХ последовательного контура
(на резонансной частоте все расстройки равны 0)
Вывод: на резонансной частоте сопротивление последовательного контура имеет наименьшее значение ФЧХ:
Вывод: на резонансной частоте последовательный контур имеет чисто активное сопротивление: Передаточные АЧХ и ФЧХ последовательного колебательного контура, его избирательные свойства. Полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы
Обычно спектр частот радиосигнала составляет 2-3% от несущей частоты, поэтому можно приблизительно считать
Вывод: на резонансной частоте коэффициент передачи последовательного контура максимальный: ФЧХ:
На выходе стоит конденсатор, поэтому напряжение выхода отстаёт от тока на 90°. Угол
Передаточная ФЧХ имеет линейный участок при расстройках от
Прохождение через колебательный контур сигналов негармонической формы. Избирательные свойства последовательного контура
Избирательность — способность цепи различать сигналы по частоте. Подадим на последовательный контур сигнал, который состоит из 5 гармоник одинаковой амплитуды. На выходе амплитуда сигнала не резонансной частоте будет максимальной, т. к. Вывод: последовательный контур обладает избирательностью по напряжению. Он выделяет сигнал резонансной частоты.
Полоса пропускания контура — область частот, на границах которой модуль комплексного коэффициента передач уменьшается в На уровне полосы пропускания коэффициент обозначается
Нарисуем передаточную характеристику
Вывод: чем выше добротность, тем уже полоса пропускания контура.
1) 2)
Кривые тока и напряжения такого вида называются резонансными. Примечание: При малых расстройках напряжение на катушке и конденсаторе можно рассчитать по формуле:
Принципиальная схема параллельного колебательного контура. Резонанс токов в параллельном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе токов. Резонансная частота, добротность Контур называется параллельным, если катушка, конденсатор и источник соединены параллельно.
В параллельном контуре может возникнуть резонанс токов, когда напряжение и ток на входе совпадают по фазе:
Проводимость индуктивная равна проводимости емкостной.
При резонансе токов сопротивление параллельного контура максимально.
Свойства цепи при резонансе токов: 1. Ток в момент резонанса:
При резонансе токов общий ток минимальный. 2. На практике
При резонансе токов токи ветвей приблизительно равны. 3. Построим векторную диаграмму для резонанса токов:
Если бы 4. Выведем формулу резонансной частоты. Для этого
Вывод: резонанс токов наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура. Получить резонанс токов можно, изменяя L или C, или частоту питающего напряжения. 5. Энергетический процесс при резонансе токов такой же, как и при резонансе напряжений:
Рассчитаем токи в момент резонанса:
Вывод: добротность в параллельном контуре показывает, во сколько раз токи ветвей больше общего тока в момент резонанса, поэтому это явление и называется резонанс тока.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 5541; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

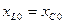




 .
.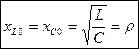 .
.





 , где
, где 

 — формула входной АЧХ последовательного контура
— формула входной АЧХ последовательного контура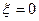



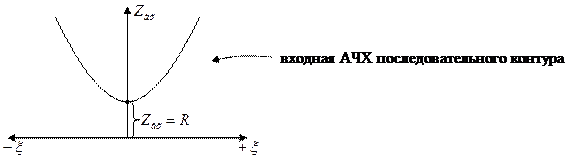

 — формула входной ФЧХ последовательного контура
— формула входной ФЧХ последовательного контура




 . На частотах больше резонансной характер сопротивления активно-индуктивный:
. На частотах больше резонансной характер сопротивления активно-индуктивный:  .
.

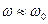

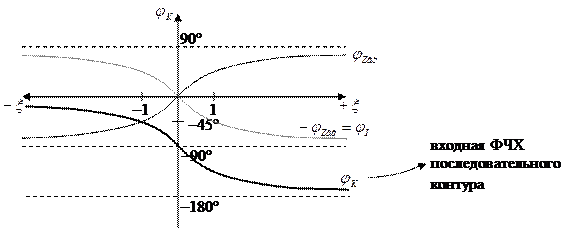
 — передаточная АЧХ последовательного контура в абсолютных координатах
— передаточная АЧХ последовательного контура в абсолютных координатах





 практически равен углу выходного напряжения, поэтому характеристику
практически равен углу выходного напряжения, поэтому характеристику  сдвигаем на 90° вниз:
сдвигаем на 90° вниз: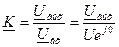
 до
до  .
.
 , и на этой частоте самый большой коэффициент передачи.
, и на этой частоте самый большой коэффициент передачи.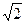 раз по сравнению с резонансным.
раз по сравнению с резонансным. :
:
 :
:

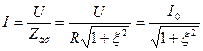
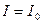


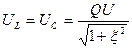

 .
.
 — условие резонанса токов
— условие резонанса токов


 ,
,




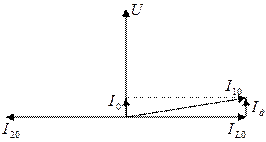
 (контур идеальный), то токи
(контур идеальный), то токи  , и общий ток был бы равен 0, но т. к. есть небольшое
, и общий ток был бы равен 0, но т. к. есть небольшое  , то существует активная составляющая тока (маленькая) и общий ток равен этой активной составляющей.
, то существует активная составляющая тока (маленькая) и общий ток равен этой активной составляющей.