
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подключение параллельного колебательного контура к источникам напряжения и тока. Избирательность параллельного колебательного контураСодержание книги
Поиск на нашем сайте
Питание параллельного контура от источника напряжения и источника тока
Если параллельный контур питается от источника напряжения с малым внутренним сопротивлением, то
Вывод: при питании от источника напряжения с малым внутренним сопротивлением параллельный контур обладает избирательностью по току, но не обладает избирательностью по напряжению. Чтобы он обладал избирательностью по напряжению, последовательно с ним включают очень большое внутреннее сопротивление
При этом источник напряжения превращается в источник тока, ток которого не зависит от сопротивления нагрузки.
Вывод: если параллельный контур питается от источника тока, то он обладает избирательностью по напряжению. Входные АЧХ и ФЧХ параллельного колебательного контура. Характер реактивного сопротивления параллельного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной
Воспользовавшись формулой
Вывод: параллельный контур имеет максимальное сопротивление на резонансной частоте. По мере увеличения расстройки сопротивление параллельного контура падает. ФЧХ:
Вывод: на резонансной частоте сопротивление контура чисто активное Передаточные АЧХ параллельного колебательного контура. Эквивалентная добротность, полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы
Для этой схемы вводят понятие эквивалентной добротности:
Появляется понятие эквивалентной обобщённой расстройки:
тогда передаточная АЧХ параллельного контура в абсолютных координатах рассчитывается:
Передаточная АЧХ в относительных координатах параллельного контура имеет вид:
Для этой схемы токи ветвей и общий ток в момент резонанса можно рассчитать по формулам:
Виды параллельных колебательных контуров. Контуры с неполным включением Автотрансформаторное (неполное) включение контура Схема контура I-го вида
Эта цепь удовлетворительно работает, если соблюдается условие На практике Чтобы это равенство соблюдалось, уменьшают
Схема контура II-го вида
Вводят понятие коэффициент включения контура:
Доказано, что
Т. к.
Схема контура III вида
Т. к.
Неполное включение контура служит для уменьшения входного сопротивления контура на резонансной частоте. Дополнение. Сравнение последовательного и параллельного контуров
Электронные аналоги колебательных контуров. Электронный колебательный контур, его избирательные свойства. Достоинства электронного колебательного контура по сравнению с пассивными колебательными контурами. Гиратор
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1918; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.219.131 (0.005 с.) |



 (видно из схемы), избирательности по напряжению нет.
(видно из схемы), избирательности по напряжению нет. в момент резонанса будет минимальный ток.
в момент резонанса будет минимальный ток. , которое:
, которое:


 , а т. к.
, а т. к.  , то
, то  будет повторять по форме
будет повторять по форме  .
.




 , и в числителе им можно пренебречь
, и в числителе им можно пренебречь
 , получим формулу входной АЧХ параллельного контура:
, получим формулу входной АЧХ параллельного контура: — формула входной АЧХ параллельного контура
— формула входной АЧХ параллельного контура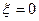








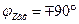
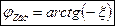 — входная ФЧХ параллельного контура
— входная ФЧХ параллельного контура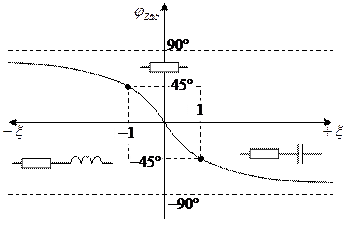
 , а на частотах меньше резонансной — активно-индуктивное,
, а на частотах меньше резонансной — активно-индуктивное,  .
.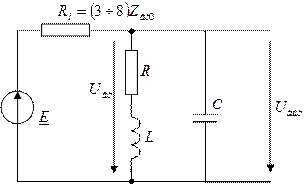
 , где
, где — собственная добротность параллельного контура
— собственная добротность параллельного контура ,
, , где
, где


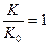








 — тоже определённая величина, поэтому это равенство может не соблюдаться.
— тоже определённая величина, поэтому это равенство может не соблюдаться.


 , то
, то 


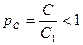
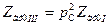
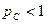 , то
, то 






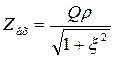

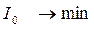
 В последовательном контуре добротность показывает, во сколько раз напряжение на реактивных элементах (на выходе) больше, чем напряжение на входе. Поэтому это явление называется резонанс напряжений.
В последовательном контуре добротность показывает, во сколько раз напряжение на реактивных элементах (на выходе) больше, чем напряжение на входе. Поэтому это явление называется резонанс напряжений.
 В параллельном контуре добротность показывает, во сколько раз ток ветвей больше общего тока в момент резонанса. Поэтому это явление называется резонанс токов.
В параллельном контуре добротность показывает, во сколько раз ток ветвей больше общего тока в момент резонанса. Поэтому это явление называется резонанс токов.



