
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колебательный контур. Свободные электромагнитные колебания в контуре. Формула Томсона.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
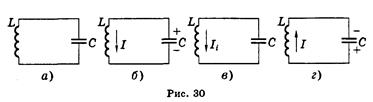
Электромагнитные колебания — это колебания электрических и магнитных полей, которые сопровождаются периодическим изменением заряда, тока и напряжения. Простейшей системой, где могут возникнуть и существовать электромагнитные колебания, является колебательный контур. Колебательный контур — это система, состоящая из катушки индуктивности и конденсатора (рис. 30, а). Если конденсатор зарядить и замкнуть на катушку, то по катушке потечет ток (рис. 30, б). Когда конденсатор разрядится, ток в цепи не прекратится из-за самоиндукции в катушке. Индукционный ток, в соответствии с правилом Ленца, будет течь в ту же сторону и перезарядит конденсатор (рис. 30, в). Ток в данном направлении прекратится, и процесс повторится в обратном направлении (рис. 30, г). Таким образом, в колебательном контуре будут происходить электромагнитные колебания из-за превращения энергии электрического поля конденсатора (Wэ = = CU2/2) в энергию магнитного поля катушки с током (wm = LI2/2) и наоборот. Период электромагнитных колебаний в идеальном колебательном контуре (т. е. в таком контуре, где нет потерь энергии) зависит от индуктивности катушки и емкости конденсатора и находится по формуле Томпсона Т = 2π√LC. Частота с периодом связана обратно пропорциональной зависимостью ν = 1/Т. В реальном колебательном контуре свободные электромагнитные колебания будут затухающими из-за потерь энергии на нагревание проводов. Для практического применения важно получить незатухающие электромагнитные колебания, а для этого необходимо колебательный контур пополнять электроэнергией, чтобы скомпенсировать потери энергии. Для получения незатухающих электромагнитных колебаний применяют генератор незатухающих колебаний, который является примером автоколебательной системы.
Колебательный контур – это электрическая цепь, в которой можно получить свободные электромагнитные колебания. К.К. состоит всего из двух приборов: катушки индуктивностью L и конденсатора электроёмкостью С. Идеальный колебательный контур не имеет сопротивления.
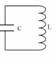
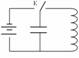
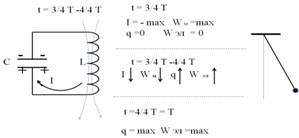
Чтобы сообщить энергию в К.К., т.е. вывести его из положения равновесия, нужно временно разомкнуть его цепь и поставить ключ с двумя положениями. Когда ключ замкнут на источник тока, то конденсатор заряжается до максимального заряда. Этим подают в К.К. энергию в виде энергии электрического поля. Когда ключ замкнут в правое положение, то источник тока отключен, К.К. предоставлен самому себе.
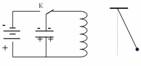
Такое состояние К.К. соответствует положению математического маятника в крайнем правом положении, когда его вывели из состояния покоя. Колебательный контур выведен из положения равновесия Заряд конденсатора – максимален и энергия заряженного конденсатора – энергия электрического поля максимальна. Будем рассматривать весь процесс, который происходит в нём по четвертям периода.
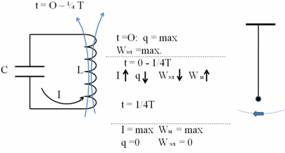
В 1-ый момент конденсатор заряжен до максимального заряда (нижняя обкладка заряжена положительно), энергия в нём сосредоточена в виде энергии электрического поля. Конденсатор замкнут сам на себя, и он начинает разряжаться. Положительные заряды по закону Кулона притягиваются к отрицательным, и возникает ток разрядки, направленный против часовой стрелки. Если бы на пути тока не было бы катушки индуктивности, то всё произошло бы мгновенно: конденсатор бы просто разрядился. Накопленные заряды компенсировали бы друг друга, энергия электрическая превратилась бы в тепловую. Но в катушке возникает магнитное поле, направление которого можно определить по правилу буравчика – «вверх». Магнитное поле - растущее и возникает явление самоиндукции, которое препятствует росту тока в нём. Ток растёт не мгновенно, а постепенно, в течение всей 1-ой четверти периода. За это время ток будет расти до тех пор, пока его поддерживает конденсатор. Как только конденсатор разрядится, ток больше не растёт, он к этому моменту достигнет максимального значения. Конденсатор разрядился, заряд равен 0, значит и энергия электрического поля равна 0. Но в катушке течёт максимальный ток, вокруг катушки существует магнитное поле, значит, произошло превращение энергии электрического поля в энергию магнитного поля. К концу 1-ой четверти периода в К.К.ток максимальный, энергия сосредоточена в катушке в виде энергии магнитного поля. Это соответствует, тому положению маятника, когда он проходит положение равновесия.
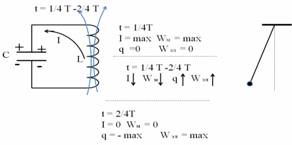
В начале 2-ой четверти периода, конденсатор разряжен, а ток достиг максимального значения и он должен был бы мгновенно исчезнуть, ведь конденсатор его не поддерживает. И ток действительно начинает резко убывать, но он течёт по катушке, и в ней возникает явление самоиндукции, которое препятствует любому изменению магнитного поля, вызывающего это явление. ЭДС самоиндукции поддерживает исчезающее магнитное поле, индукционный ток имеет то же направление, что и существующий. В К.К. ток течёт против часовой стрелки – в пустой конденсатор. В конденсаторе накапливается электрический заряд - на верхней обкладке – положительный заряд. Ток течёт до тех пор, пока его поддерживает магнитное поле, до конца 2-ой четверти периода. Конденсатор зарядится до максимального заряда (если не произойдёт утечки энергии), но противоположного направления. Говорят, конденсатор перезарядился. К концу 2-ой четверти периода ток исчезает, значит, энергия магнитного поля равна 0.Конденсатор перезарядился, его заряд равен (– максимальному). Энергия сосредоточена в виде энергии электрического поля. В течение этой четверти произошло превращение энергии магнитного поля в энергию электрического поля. Состояние колебательного контура соответствует такому положению маятника, при котором он отклоняется в крайнее левое положение.
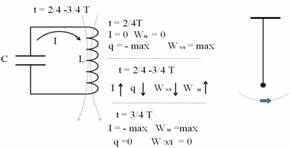
В 3-ей четверти периода происходит всё также, что и в 1-ой четверти, только противоположного направления. Конденсатор начинает разряжаться. Ток разрядки растёт постепенно, в течение всей четверти, т.к. быстрому росту его препятствует явление самоиндукции. Ток растёт до максимальной величины, пока конденсатор не разрядится. К концу 3-ей четверти энергия электрического поля превратится в энергию магнитного поля, полностью, если не будет утечки. Это соответствует такому положению маятника, когда он снова проходит положение равновесия, но в противоположном направлении.
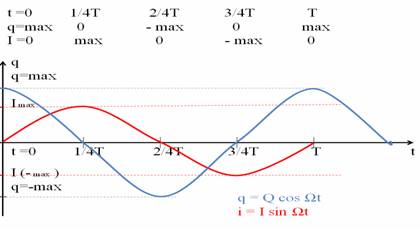
В 4-ой четверти периода происходит всё так же, как и во 2-ой четверти, только в противоположном направлении. Ток, поддерживаемый магнитным полем, постепенно убывает, поддерживаемый ЭДС самоиндукции и перезаряжает конденсатор, т.е. возвращает его к первоначальному положению. Энергия магнитного поля превращается в энергию электрического поля. Что соответствует возвращению математического маятника в первоначальное положение. Анализ рассмотренного материала: 1. Можно ли колебательный контур рассматривать, как колебательную систему? Ответ: 1. В колебательном контуре происходит превращение энергии электрического поля в энергию магнитного поля и наоборот. 2. Явление самоиндукции играет роль возвращающей силы. Поэтому колебательный контур рассматривать, как колебательную систему. 3. Колебания в К.К. можно считать свободными. 2. Можно ли колебания в К.К. рассматривать, как гармонические? Анализируем изменение величины и знака заряда на обкладках конденсатора и мгновенного значения тока и его направления в цепи.
На графике видно: Заряд и сила тока изменяются по гармоническому закону, и мы можем записать соответствующие законы. Фазы колебаний тока и заряда не совпадают. Заряд опережает ток по фазе на 3. Что в колебательном контуре колеблется? Какие физические тела совершают колебательные движения? Ответ: колеблются электроны, они совершают свободные колебания. 4. Какие физические величины изменяются при работе колебательного контура? Ответ: изменяются сила тока в цепи, заряд в конденсаторе, напряжение на обкладках конденсатора, энергия электрического поля и энергия магнитного поля. 5. Период колебаний в колебательном контуре зависит только от индуктивности катушки L и ёмкости конденсатора C. Формула Томсона: Т = 2π Билет № 12
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 1526; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.245.172 (0.006 с.) |

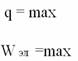
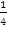 периода.
периода. можно сравнить и с формулами для механических колебаний.
можно сравнить и с формулами для механических колебаний.


